构造法解决“等差数列前n项和”问题

袁琰　苏建伟　乔雅童

摘要：构造法的灵活运用，能激发学生学习数学的兴趣，进而发展学生的创造性思维.本文通过构造的方法把“等差数列求前n项和”的四题转化成求图形面积的问题，并引用特殊的案例整理出一般等差数列的求和的思路与方法，以形助数，培养学生的几何直观能力.

关键词：等差数列前n项和；等差数列；构造法；图形面积

数列指按照确定的顺序排列的一列数，常以“找规律”的形式出现在小学与初中阶段的数学教学与学习中，更是高中知识体系的重要组成部分.高中阶段主要运用函数的思想方法研究数列，通过把数列看成一类特殊的函数来探索它们的规律.大家对于10岁的高斯巧妙求1＋2＋3＋…＋100的故事耳熟能详，这也引发人们对等差数列求前n项和问题的思考，高斯与现有高中数学教材采用的都是倒序相加法求等差数列前n项和.本文采用“构造法”给出等差数列求和的新思路，即从数形结合的思想出发，以形助数，通过构造图形求面积的方法来解决等差数列求和的问题［1］，将等差数列求和的数量关系与几何图形建立联系.

构造法的灵活运用，能激发学生学习数学的兴趣，培养学生的创造性思维，进一步提高学生应用数学方法分析和解决问题的能力.利用构造图形的方法解决等差数列求和问题，化抽象为具体，提高学生在数感和几何直观方面的能力.同时学生通过多种思路去解决实际应用问题，提高学生的抽象思维能力.

1等差数列求和的特殊案例

本文根据等差数列首项与公差的正负情况将其求和问题用以下6个案例来进行构造法思想的展示.

1.1首项与公差都等于1的情况

“1+2+3+4+5”，此例的首项与公差都为1.对该例采用构造法：“1”表示一个边长为1的单位正方形的面积、“2”表示两个单位正方形面积、“3”表示三个单位正方形面积……以此类推［2］；并将所有的单位正方形由首项到末项进行自上而下的摆放：第一层1个、第二层2个、第三层3个、第四层4个、第五层5个，如图1所示.

此时等差数列求和的问题化成了求图1图形面积的问题，不妨令首项a1=c+d，其中d表示公差，末项为a_n，正方形排列的总层高为h.将图1中的图形划分为如图2所示的大三角形与小三角形两个主要部分，其中阴影部分大三角形的面积设为S₁，剩余所有的小三角形的总面积设为S₂，整个图形的面积设为S.

1.2首项与公差都大于0，且首项为1而公差不为1的情况

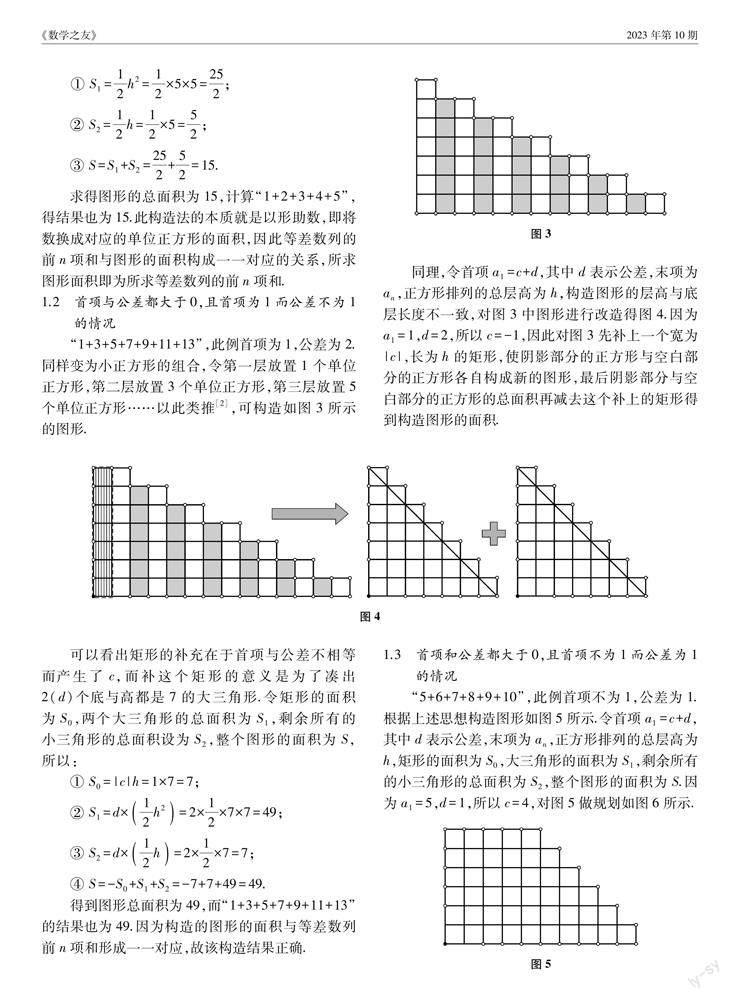
“1+3+5+7+9+11+13”，此例首项为1，公差为2.同样变为小正方形的组合，令第一层放置1个单位正方形，第二层放置3个单位正方形，第三层放置5个单位正方形……以此类推［2］，可构造如图3所示的图形.

同理，令首项a₁=c+d，其中d表示公差，末项为an，正方形排列的总层高为h，构造图形的层高与底层长度不一致，对图3中图形进行改造得图4.因为a₁=1，d=2，所以c=-1，因此对图3先补上一个宽为|c|，长为h的矩形，使阴影部分的正方形与空白部分的正方形各自构成新的图形，最后阴影部分与空白部分的正方形的总面积再减去这个补上的矩形得到构造图形的面积.

1.3首项和公差都大于0，且首项不为1而公差为1的情况

“5+6+7+8+9+10”，此例首项不为1，公差为1.根据上述思想构造图形如图5所示.令首项a₁=c+d，其中d表示公差，末项为an，正方形排列的总层高为h，矩形的面积为S₀，大三角形的面积为S₁，剩余所有的小三角形的总面积为S₂，整个图形的面积为S.因为a₁=5，d=1，所以c=4，对图5做规划如图6所示.

1.4首项与公差都大于0，且首项与公差都不为1的情况

1.5首项小于0，但公差为1的情况

1.6首项小于0，但公差大于0且不为1的情况

2构造法求等差数列和的一般思路

本文根据上述特殊案例的图形构造过程，将等差数列求和按照首项和公差的正負分成以下四种情况，对构造图形求数列和的思路进行总结，并结合等差数列求和的公式来说明该构造法的可行性与真实性.

2.1首项、公差都大于0的情况

2.2首项、公差都小于0的情况

2.3首项小于0，但公差大于0的情况

2.4首项大于0，但公差小于0的情况

3结语

本文通过构造法，将等差数列求和的代数问题赋予几何意义，使数量关系与几何图形建立联系.以数形结合的方式将四种不同情况下构造的图形的面积来解释等差数列求和问题，且每种情况的思路都万变不离其宗，即求矩形、大三角形和小三角形的面积.虽然这种构造方式放在高中数学教学与学习中并不简便，但却给学生提供一种更加直观的解题方式，培养了学生的创新思维与几何直观能力.

几何直观是将抽象的模型具体化，通过分析问题将题中条件利用图形进行描述，从而把复杂的数学问题变得简明、形象，有助于学生直观地理解数学，打开解决问题的思路，预测结果［3］，它是数学学习的重要能力.“构造法”是用一类问题的性质去探究另一类问题性质的解题方法［4］.学生几何直观能力的培养是个漫长的过程，需要融入到具体的知识内容中，使抽象化的问题具体化，激发学生的探究意识，鼓励学生从不同的角度去思考数学问题；而构造法解题的关键是构造，其基本思想是转化，也是鼓励学生多角度地思考数学问题［5］.因此，教师在教授过程中要注意几何直观的渗透，通过几何直观能力的培养来锻炼学生的创新思维，让学生从特殊的案例中归纳出一般的求解思路，从代数的抽象知识中感受到几何的直观性，建立清晰的逻辑体系，体会数形结合的思想方法，培养和提高学生的数学核心素养.参考文献：

［1］ 戚洪祥.构造法解决数列求和问题［J］.中小学数学（小学版），2021（10）：2123.

［2］ 王彬，吴谦，侯晓婷，李春兰.基于数形结合思想的“等差数列的前n项和”教学设计［J］.数学教学，2021（6）：1723.

［3］ 苏建伟，李鹏.国内几何直观研究综述［J］.海南广播电视大学学报，2017，18（1）：144150.

［4］ 潘光明，高秀军.构造法在解题中的应用［J］.数学教学通讯，1992（3）：1820.

［5］ 李红春.转换视角多联想构造引出妙法来［J］.数学教学研究，2013，32（9）：4446+50.