2022年高考甲卷理数20题的探究及背景分析

王东海

(安徽省肥东县城关中学,安徽 合肥 231600)

一道好的数学试题,不但注重在知识交汇处命题,而且立足于考查考生的关键能力和数学学科核心素养.2022高考全国甲卷第20题就是这样的一道试题,它既具有基础性,又具有创新性,试题极具选拔功能.

1 真题呈现

题目设抛物线C:y2=2px(p>0)的焦点为F,点D(p,0),过点F的直线交C于M,N两点．当直线MD垂直于x轴时,|MF|=3．

(1)求C的方程;

(2)设直线MD,ND与C的另一个交点分别为A,B,记直线MN,AB的倾斜角分别为α,β．当α-β取得最大值时,求直线AB的方程．

分析此题第(2)小题涉及直线MN,AB的倾斜角,首先应与直线的斜率联系起来,导出MN,AB的斜率的倍数关系,再考虑使用α-β的正切公式,即可求出tan(α-β)的最大值.除了这种代数法以外,我们还可尝试使用几何法加以解决.

2 解法探究

思路1(1)易知C:y2=4x.(2)根据题意如何找到直线MN和AB的斜率的关系是解题的关键.

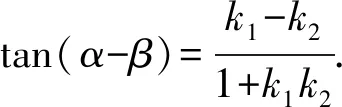
图1 解法1图

令M(x1,y1),N(x2,y2)(y1>0,y2<0),A(x3,y3),B(x4,y4)(y3<0,y4>0),

AB:y=k2(x-m),

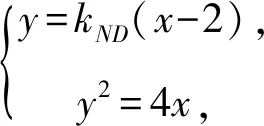
故k1=2k2.

又易得x3x4=16x1x2=m2,所以m=4.

点评这里也可不求T坐标,转而求线段AB中点坐标,也可很快求出.实际上该题蕴含着抛物线任意弦的两个端点的横坐标之积等于此弦与x轴交点横坐标的平方.如果能够提前掌握该性质,则能够为我们解题指明方向,从而提高效率.

思路2解法1运算量较大,能否不设直线方程,而用点去表示直线从而求解此题.

解法2(点参法)令M(x1,y1),N(x2,y2),A(x3,y3),B(x4,y4),故

化简,得4x-(y1+y2)y+y1y2=0.

因过点(1,0),代入得y1y2=-4.

同理MA:4x-(y1+y3)y+y1y3=0,

NB:4x-(y2+y4)y+y2y4=0.

将所过定点D(2,0)代入,得

y1y3=-8,y2y4=-8.

思路3 观察到本题出现了直线的倾斜角,我们联想到直线的参数方程,从而考虑用角作为参数来处理该题.

所以sin2α·t-4cosα·t-4=0.

思路4 观察图中出现的4条直线,其中3条经过定点,因此可以考虑设过点T(m,0)的直线系方程,避免多次联立.

解法4由题意设过点T(m,0)的直线系方程为y=k(x-m).

当m=2时,yMyA=-8,yNyB=-8.

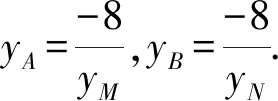
思路5 该题除去坐标法外,还可考虑几何法处理,从几何图形观察知,抛物线内接四边形像一个蝴蝶形状,可考虑用蝴蝶定理加以解决[1].

引理1 如图2,设D为圆内弦PQ的中点,过点D作弦MA,NB,设MN,AB分别交弦PQ所在直线于点X,Y,则点D是XY的中点.另圆可以改为任意圆锥曲线,结论亦成立.

图2 引理1图

解法5如图3,过点D作直线DQ垂直x轴,交MN延长线于点X,交BA延长线于点Y,交抛物线于P,Q两点.

图3 解法5图

因为PD=QD,由蝴蝶定理可知XD=YD.

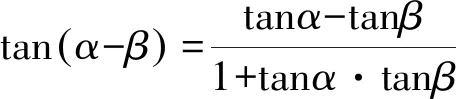
由解法1知,y3=2y2,y4=2y1,y1y2=-4.

即AB过定点T(4,0).

故DT=4-2=2.

从而tanα=2tanβ.下同解法1.

思路6 注意观察直线MN,AB的交点,能否用交点的轨迹去处理?

解法6 如图4,设MN,AB交点J(x,y),由解法2知,直线MN:4x-(y1+y2)y+y1y2=0.

图4 解法6图

①

直线AB:4x-(y3+y4)y+y3y4=0,

即4x-2(y1+y2)y+4y1y2=0.

②

①×2-②,得4x+2y1y2-4y1y2=0.

所以4x=2y1y2=-8,即x=-2.

故交点J的轨迹是直线x=-2.

又由前知点T(4,0),

故kMN=2kAB.下同解法1.

3 背景分析

通过对这道考题的解答,并观察此题,发现图形呈蝙蝠状,故称其为蝙蝠模型.如图2,发现四边形MNAB是抛物线的内接四边形,那么由极点极线的知识,直线MN和直线AB的交点J必在点D对应的极线上,同理另一组对边AN和BM延长线的交点I也在极线上,而点D对应的极线方程为0·y=2(2+x),即x=-2上.

4 拓展探究

细品解题过程,笔者发现第(2)问的解答耐人寻味,值得探究.于是笔者思考,对于一般性的抛物线,将点D的坐标一般化时,会推导出什么结论呢?若焦点F变成其他x轴上定点时呢?如果背景的圆锥曲线换成椭圆、双曲线,是否仍有类似的结论呢?基于以上思考,笔者探究得到如下结论:

证明设点A(x1,y1),B(x2,y2),P(x3,y3),Q(x4,y4),由抛物线性质知x1·x2=t2,x1·x3=m2,x4·x2=m2.

结论1是结论2的特殊情况,证明方法类似,这里略去.

引理2若过点S(n,0)的直线与抛物线y2=2px(p>0)交于点M,N,点D(m,0),直线MD,ND分别交抛物线于点A,B,又AB交x轴于点T, 且点D对应的极线l交x轴于点H,则H,S,D,T四点成调和点列,即HS·DT=HT·SD(如图5).

图5 引理2图

证明因为点D(m,0)对应的极线方程为0·y=2(m+x),即x=-m.故点H(-m,0).

故HS·DT=HT·SD.

当然这里根据极点、极线的性质直接证明也可,设直线MN,AB交于点J,连接JD,在△JBK中,x轴与ΔJBK的四个交点为H,S,D,T,由极点、极线的性质知必成调和点列.即HS·DT=HT·SD.

引理3若过点S(n,0)的直线与圆锥曲线交于点M,N,点D(m,0),直线MD,ND分别交圆锥曲线于点A,B,又AB交x轴于点T, 且点D对应的极线l交x轴于点H,则H,S,D,T四点成调和点列,即HS·DT=HT·SD.

证明方法同引理2类似,这里略.

图6 结论3图

上面我们探究了已知直线AB过定点,可推导出kMN和kAB的比值为定值.下面我们还可以探究它的逆命题是否成立?

③

④

那么椭圆和双曲线有无类似逆命题呢?感兴趣的读者可进一步去探究.

在数学教学中,时常会遇到各种各样的问题,这时我们不能满足于将问题解决了就万事大吉,而是要进一步进行探究.我们可以进行解法探究,也可以将问题一般化进行拓展研究,还可以进行变式研究.在教学中,要为学生提供探究的机会,让学生在探究中体会到学习的快乐,让探究成为一种习惯[2].