例谈求解二面角大小的几种方法
解 曼 房维维
(哈尔滨师范大学,黑龙江 哈尔滨 150025)
中学数学中的二面角是立体几何的基础概念,值得学生思考重视,对于学生而言,只有在平时学习中多多积累求解二面角的方法,才能在问题探索中不断提高解题能力,提高数学核心素养.本文对求解二面角的方法进行归纳和总结,以供读者借鉴和参考.
1 定义法
在定义法中,二面角的大小是用二面角的平面角来衡量的,就是在平面α和平面β的交线l上找一点,过该点在平面α和平面β内分别作垂直于棱的两条射线.如图1,射线OA与射线OB所夹的角∠AOB就是所求的二面角.在定义法中,二面角的大小是用二面角的平面角来衡量的.
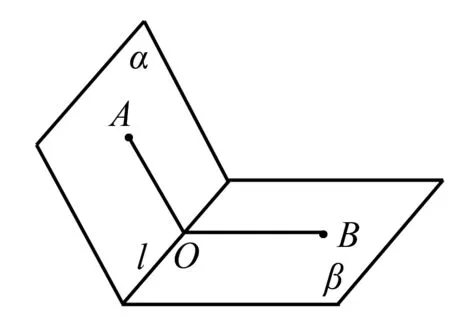
图1 二面角图
适用范围:定义法是最直接的做法,它适用于比较明显的两个平面相交图形,在解题时只需要找出两个平面、两个射线及射线夹角即可,对于不太容易找出射线的图形可以借助辅助线来解决,如例1中的图形[1].
例1如图2,在三棱锥S-ABC中,∠SAB=∠SAC=∠ABC=90°,SA=AB,SB=BC,求二面角A-SC-B的平面角的正弦值.
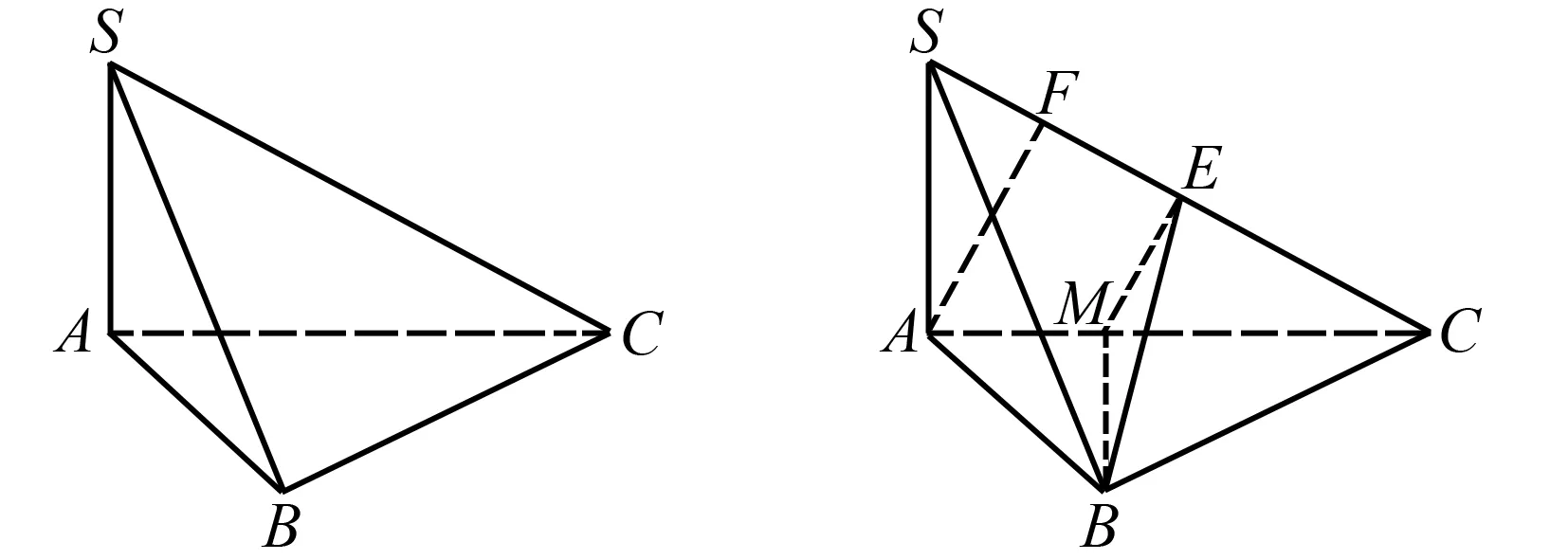
图2 例1图 图3 例1定义法解析
解析如图3,取SC中点E,连接BE,
因为SB=BC,
所以△SBC是等腰三角形.
由等腰三角形三线合一知BE⊥SC.
过点A作AF⊥SC于点F,过点E作EM∥AF交AC于点M,连接BM,此时∠MEB就是所求的二面角的平面角.
设SA=2,则AB=2.
因为∠SAB=90°,
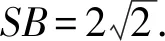
因为∠ABC=90°,
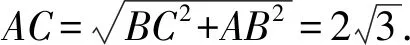
因为∠SAC=90°,

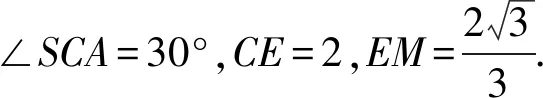
由面积相等,知
因为△CEM∽△CFA,



由余弦定理,知
BM2=AM2+AB2-2AM·ABcos∠CAB

2 补形法
这种方法也是求解二面角大小的重要方法,通过补形能够顺利地作出二面角的平面角,从而整体上把握点、线、面之间的关系,与定义法有异曲同工之妙.
适用范围:补形法顾名思义适用规则不完整的图形,利用辅助线将平面的图形完整化,使之有明确的交线,然后进行解题[2].
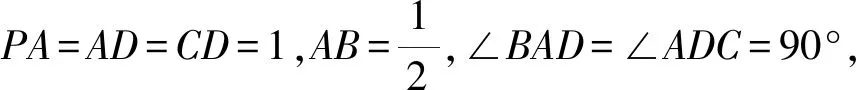

图4 例2图 图5 例2解析图

所以AB∥CD,CD⊥AD,AB⊥AD,AE=AD=1.
因为PA⊥平面ABCD,
所以PA⊥AB,PA⊥AD,DE=AE+AD=2.

所以DE2=PE2+PD2.
即PE⊥PD.
因为PA∩AD于点A,
所以AB⊥平面PED,CD⊥平面PED.
所以CD⊥PE,CD⊥PD.
因为PD∩CD于点D,
所以PE⊥平面PCD.
所以PE⊥PC.
又因为PE⊥PD,
所以∠CPD就是平面PAD和平面PBC所成的二面角.

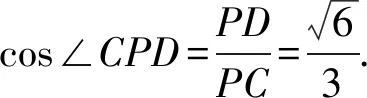

以上是在图形中找二面角的平面角从而求出二面角的大小,除此之外,还可以用公式法来求解二面角,公式法的特点是代入公式中就可直接求出二面角的大小,使用方便,下面给出两种用公式求二面角的方法[3].
3 射影面积法

适用范围:这种方法适合一个面在另一个面内的投影确定的图形[4],对于这种方法我们依旧看例1.
解析如图6,过点B作BD⊥AC于点D,
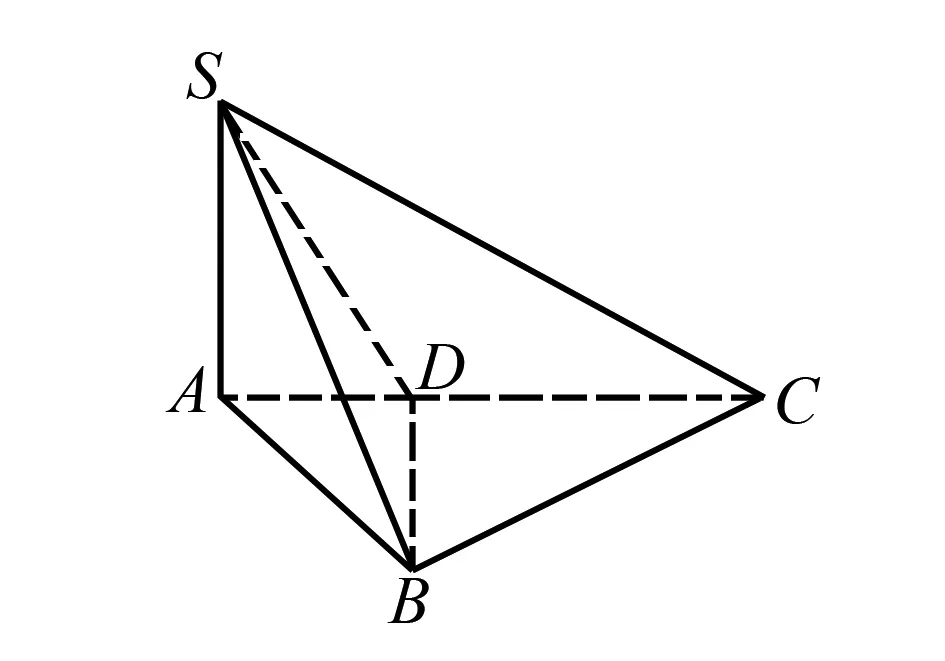
图6 例1射影面积法图
因为∠SAB=∠SAC=∠ABC=90°,
所以SA⊥AB,SA⊥AC.
所以SA⊥平面ABC.
所以SA⊥BD.
又因为BD⊥AC,
所以BD⊥平面SAC.
所以△SDC是△SBC在平面SAC内的投影.

设二面角A-SC-B的平面角为θ,


4 向量法
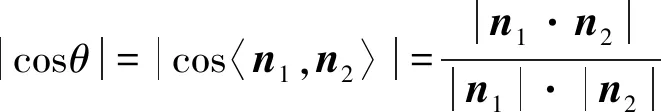

图7 两条法向量方向相同时 图8 两条法向量方向相反时
适用范围:向量法适用于所有能作平面直角坐标系的图形,通过找出两个半平面的法向量进而解出题目.其中,直角坐标系的建立是基础,而判断两平面的法向量是相等还是互补是难点和关键[5].
例3 如图9所示,正方体ABCD-A1B1C1D1的棱长为1,求二面角A1-BD-C1的余弦值.

图9 例9图


设平面DA1B的法向量为m=(x,y,z),则
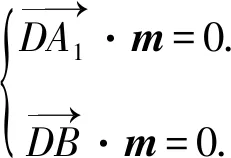
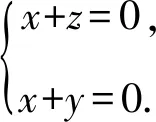
所以m=(1,-1,-1).
设平面DBC1的法向量为n=(a,b,c),则
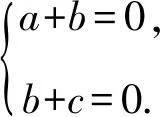
所以n=(-1,1,-1).
设平面DA1B和平面DBC1所成的二面角为θ,
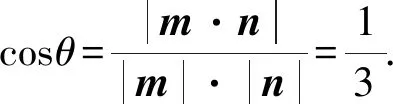

以上就是求解二面角大小的四种方法即相应的例题,在求解二面角的大小时可以根据不同的题型采取不同的方法,其中有的题型可以用多种方法来进行解决,需要视情况而定.

