基于两道高考概率题的深入思考

张军伟

(东北师范大学附属中学,吉林 长春 130021)

概率是高考重点考查的内容之一,试题常以实际生活问题为背景,与其他知识融合、渗透,情境新颖,充分体现了概率的工具性和应用性.综合来看,试题难度中等,不仅考查学生的基础知识和基本技能,更着重考查学生对概率知识的运用能力.在教学中对经典概率高考题进行深度剖析,有利于学生进一步完善解决概率问题的基本思路,优化运算求解过程,提高解题效率.

1 试题呈现

(1)求甲连胜四场的概率;

(2)求需要进行第五场比赛的概率;

(3)求丙最终获胜的概率.

题2 (2006年高考全国Ⅱ卷第18题)某批产品成箱包装,每箱5件．一用户在购进该批产品前先取出3箱,再从每箱中任意抽取2件产品进行检验．设取出的第一、二、三箱中分别有0件、1件、2件二等品,其余为一等品．

(1)求抽检的6件产品都是一等品的概率;

(2)若抽检的6件产品中有2件或2件以上二等品,用户就拒绝购买这批产品,求这批产品被用户拒绝的概率．

2 试题分析

两道高考题均以生活情境为背景,充分体现了数学的应用性.在知识方面,前者考查相互独立事件、互斥事件的概率计算,后者考查古典概型、相互独立事件、互斥事件的概率计算;在能力方面,两者都深度考查学生分析问题和解决问题的能力,考查层次分明、区分度较高,能使学生充分展示理性思维的广度和深度;在素养方面,均考查学生数学抽象、逻辑推理、数学运算以及数据分析等数学核心素养[1].

3 解法探究

3.1 题1解析

分析1 首先要弄清楚复杂的赛制,也就是弄清楚一次试验,可以画出每场比赛赢者的树状图.

例如,画出从第一场甲赢开始的各场次赢者的树状图(如图1),类比得出第一场乙赢的情形.

图1 分析1图

从中可以得出:①比赛至少需要进行四场比赛,至多需要进行五场比赛;

②若甲赢,则打四场全赢,或打五场,前四场输一场,第五场赢,乙赢同理;

③若丙赢,则打四场,第2,3,4场赢,或打五场,从第二场开始的三场比赛输一场,第五场赢.

所以需要进行第五场比赛的概率为

比赛五场结束且丙最终获胜,则从第二场开始的四场比赛按照丙的胜、负、轮空结果有三种情况:胜胜负胜,胜负空胜,负空胜胜,概率分别为

分析2 由于赛制规定累计负两场者被淘汰,因此画出每场比赛负者的树状图更贴合题意.

例如,画出从第一场甲胜乙开始的各场次胜负的树状图(如图2),如甲胜乙记作甲>乙,类比得出第一场乙胜甲的情形.

图2 分析2图

从中可以得出:①比赛至少需要进行四场比赛,至多需要进行五场比赛;

②某选手负两场即被淘汰,轮空制下不能连续负两场,除非已经淘汰了一位选手;

③若甲赢,则打四场,乙、丙各负两场,或打五场,前四场只能输一场,第五场赢,乙赢同理;

④若丙赢,则打四场,甲、乙各负两场,或打五场,从第二场开始的三场比赛只能输一场,第五场赢.

(2)设A为甲输,B为乙输,C为丙输,则打四场比赛结束有四种情形:BCBC,ACAC,ABAB,BABA,所以需要进行第五场比赛的概率为

(3)设A为甲输,B为乙输,C为丙输,则丙最终获胜的概率有两类情形:一类是打四场胜ABAB,BABA;另一类是打五场胜ACBAB,ABCAB,ABACB,BCABA,BACBA,BABCA,ACABB,BCBAA,ABCBA,BACAB.所以丙最终获胜的概率为

3.2 题2解析

解法1(1)设A=“抽检的6件产品都是一等品”,则

(2)设B=“这批产品被用户拒绝”,则

分析2 如果把一次试验理解成分别从第二、三箱中各任意抽取2件产品,彼此相互独立,那么就可以结合相互独立乘法公式及互斥事件加法公式进行计算.

解法2 (1)设A=“抽检的6件产品都是一等品”,则

(2)设B=“这批产品被用户拒绝”,则

分析3如果把一次试验理解成分别从第二、三箱中各任意抽取2件产品,彼此相互独立,而从每箱取产品第一次、第二次不相互独立,那么就可以结合条件概率变形公式及互斥事件加法公式进行计算.

解法3 (1)设A=“抽检的6件产品都是一等品”,则

(2)设B=“这批产品被用户拒绝”,则

4 变式练习

为了加强学生对某一类问题的掌握,适当地对同类题目加以练习,会起到强化解题思想方法的积极作用.让学生在亲身实践中寻求变通,悟出其中的来龙去脉,掌握科学的解题规律和法则,进而培养学习的兴趣和提高解题的信心.下面给出两道高考试题供读者参考.

练习1 (2019年全国Ⅱ卷理18题)11分制乒乓球比赛,每赢一球得1分,当某局打成10∶10平后,每球交换发球权,先多得2分的一方获胜,该局比赛结束．甲、乙两位同学进行单打比赛,假设甲发球时甲得分的概率为0.5,乙发球时甲得分的概率为0.4,各球的结果相互独立．在某局双方10∶10平后,甲先发球,两人又打了X个球该局比赛结束．

(1)求P(X=2);

(2)求事件“X=4且甲获胜”的概率．

解析(1)X=2就是某局双方10∶10平后,两人又打了2个球该局比赛结束,则这两个球均由甲得分,或者均由乙得分.因此P(X=2)=0.5×0.4+(1-0.5)×(1-0.4)=0.5.

(2)X=4且甲获胜,就是某局双方10∶10平后,两人又打了4个球该局比赛结束,且这4个球的得分情况为:前两球是甲、乙各得1分,后两球均为甲得分.

因此所求概率为[0.5×(1-0.4)+(1-0.5)×0.4]×0.5×0.4=0.1.

练习2 (2015年湖南理18题)某商场举行有奖促销活动,顾客购买一定金额商品后即可抽奖,每次抽奖都从装有4个红球、6个白球的甲箱和装有5个红球、5个白球的乙箱中,各随机摸出1个球,在摸出的2个球中,若都是红球,则获一等奖;若只有1个红球,则获二等奖;若没有红球,则不获奖．

(1)求顾客抽奖1次能获奖的概率;

(2)若某顾客有3次抽奖机会,记该顾客在3次抽奖中获一等奖的次数为X,求X的分布列和数学期望．

解析(1)设B1={顾客抽奖1次获一等奖},B2={顾客抽奖1以获二等奖},C={顾客抽奖1次能获奖}.

(2)X分布列为

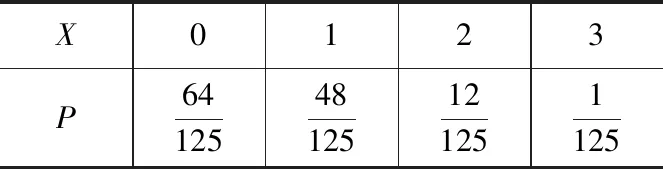
X0123P6412548125121251125

5 教学启示

通过对两道高考真题的剖析和解答,我们知道破解这类题型的关键是突破试题的情境、理解题意,然后建立正确的概率模型,结合概率计算公式,就能顺利求解.我们在教学过程中要注重落实好以下几方面内容:

5.1 依托实例,完善体系

在概率教学过程中,自始至终都要结合实例展开.教学中应提供丰富的、典型的随机现象实例,鼓励学生提出有价值的概率问题,使学生经历随机现象—随机试验—随机事件的学习过程,真正搞清楚不同随机事件的区别与联系,进而建立对高中阶段概率学习的知识体系.体现在解题中,学生往往对试题中涉及的随机试验下的随机事件分析不清楚,不能准确地转化为相应的概率模型.因此教学中要加强训练,使学生积累解题经验,完善概率认知体系,提高分析随机现象的能力.

5.2 掌握模型,熟练方法

概率的基本性质是概率论的重要理论基础,它直接给出了概率的计算方法,一是由互斥事件的和事件的概率加法公式直接求,二是由对立事件的减法公式间接求.类型上古典概型的特点是样本点有限、等可能,相互独立事件常以概率不变为标志,再结合具体的随机试验可以梳理出抛硬币、掷骰子、取球、比赛等模型.教学时可筛选高考真题讲练,引导学生的解题思路——随机试验有哪些情形、样本点是什么、是否有限、是否概率不变,使学生掌握不同事件概率的求解思路以及相关的运算技巧,从而转化为相应的概率模型进行计算.同时计算较复杂事件的概率,要使学生养成利用二维表或树状图表示试验结果的好习惯,辅助学生全面地把握题意.

5.3 提炼思想,提高能力

概率是研究随机现象规律的学科,它为人们认识客观世界提供了重要的思维模式和解决问题的方法.教师在教学中需要关注:(1)关注学生审题能力,提升学生的数学抽象与直观想象的数学素养,培养学生发现问题和提出问题的能力;(2)渗透培养数学建模能力,引导学生根据实际问题构建概率模型,分析数据,提升学生数据分析和数学建模能力,培养学生分析问题、解决问题的能力;(3)重视数据计算,规范学生的解题习惯和思维训练,提升学生的逻辑推理和数学运算能力,培养学生解决问题的能力．概率素养是学生在掌握知识的基础上,经过反复实践与反思而后逐渐深化形成,于是在教学中需要渗透思维训练,培养学生学习概率的兴趣和提升其概率素养[2]．

总之,在教学过程中,教师要促进发展学生认识不确定现象的思维模式,使学生学会辩证地思考问题,成为善于认识问题、解决问题的人才.