三点共线时线段长度乘积的计算策略
朱贤良
(长沙市周南梅溪湖中学,湖南 长沙 410205)
文章先从一道解析几何中的经典问题的求解说起.
1 转换视角:简单题中也有大智慧
例1 如图1,过点M(2,1)作一直线l分别与x轴、y轴的正半轴相交于A,B两点,求|MA|·|MB|的最小值.

图1 例1图
在学习直线的方程知识时,我们常选用本题来引导学生选择合适的直线方程进行解题.本题的求解思路是先设出直线的方程,得出A,B两点的坐标,再根据两点间距离公式得到乘积|MA|·|MB|,最后求得最小值.具体解法如下:
解析设直线l的点斜式方程为
y-1=k(x-2)(k<0),


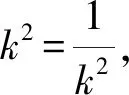


比如本题中,


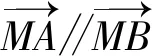


学过直线的参数方程后,我们还常利用参数t的几何意义来解决线段的长度问题,这样就有了下面的解法:

将坐标轴所在曲线方程写成xy=0,
将其与直线l联立可得
(2+tcosα)(1+tsinα)=0.
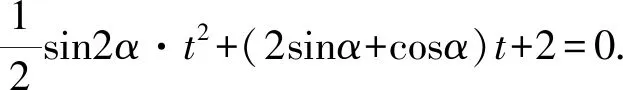


综观上述问题的不同求解思路,我们不难将三点共线时线段长度之积问题的破解方法归纳为以下三种:
(1)两点间距离公式法:先求出两点的坐标,或是“设而不求”,再借助两点间距离公式计算距离.这也是解决长度问题的通法,求解时要注意恰当借助两点间距离公式的“2.0版本”来减少运算量.
(2)向量数量积法:三点共线时,两个向量数量积的绝对值与其模的乘积相等,由此将线段长度之积转化为向量的数量积问题.

2 应用举例:心中若有法,难题亦无忧
掌握了以上三种方法,即使是面对模考与高考中的压轴题,也可以从容应对、泰然处之.

(1)求椭圆C的方程;

图2 例2图

解法1 (两点间距离公式法)


故MN的方程为

再设M(x1,y1),N(x2,y2),
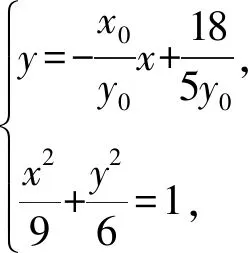

由两点间距离公式可知,
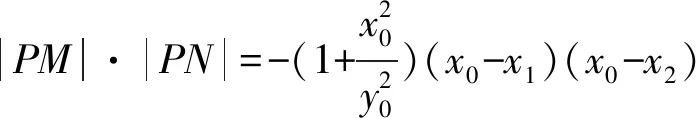

解法2 (向量数量积法)
①当切线MN的斜率不存在时,同解法1.
②当切线MN的斜率存在时,
=(x1-x0)(x2-x0)+(y1-y0)(y2-y0)


解法3 (参数方程法)

将直线MN的方程与椭圆C的方程联立,得

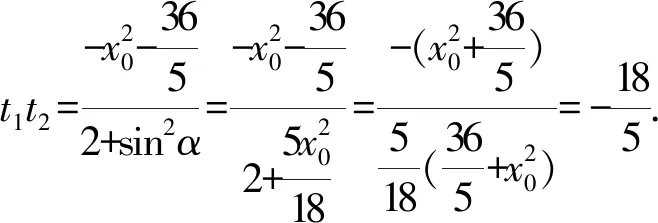

(1)求C的方程;


图3 例3图

对于第(2)问,涉及T,A,B三点共线、T,P,Q三点共线时的线段长度之积|TA|·|TB|与|TP|·|TQ|,依次采用前述三种方法进行求解:
解法1 (两点间距离公式法)

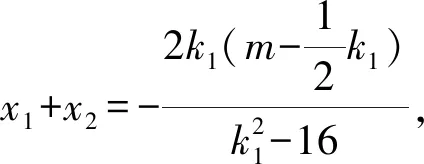

结合两点间距离公式,可得

又因为|TA|·|TB|=|TP|·|TQ|,


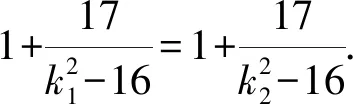
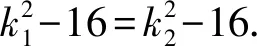

由题知k1≠k2.所以k1=-k2.
即直线AB的斜率与直线PQ的斜率之和为0.
解法2 (向量数量积法)
同解法1得


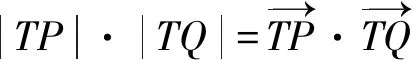
以下同解法1[2].
解法3(参数方程法)

(16cos2α-sin2α)t2+(16cosα-2msinα)t-(m2+12)=0.
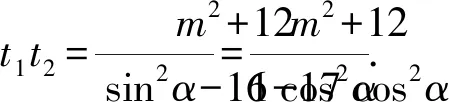
由参数的几何意义可知
再设直线PQ的倾斜角为β,同理可得
依题意,得
则cos2α=cos2β.
即cosα=-cosβ.
故α+β=π.
从而直线AB的斜率与直线PQ的斜率之和为0[4].
3 解题启示:小题大做、发散思维是提高解题能力、学好数学的重要途径
解题是数学学习的重要方面,从某种意义上说,数学能力的高低可以直接通过解题水平的高低表现出来.正如著名数学教育家波利亚所说的那样,“掌握数学就意味着善于解题.”因此,在高中数学学习中首要的目标是必须学会思考,掌握分析问题、解决问题的思维方式,提升思维品质.
日常学习过程中,通过小题大做来发散思维就是加深对数学思想和方法领悟的一个好方法.当我们遇到一些简单的小题时也会有不一样的灵感,感觉从不同途径入手都能解决问题.这往往意味着问题背后有着丰富的背景,此时我们不应放过这份灵感,而应该更加深入地去思考,进行一些探究式、发散式的学习.小题大做的目的就在于利用发散思维打通不同知识模块之间的壁垒,又或者完成从特殊到一般的延展.这样主动学习一个小问题所带来的解题能力乃至数学水平的提升,可能远远超过对一份试卷的机械刷题.
解题是提升数学能力的手段,而不是数学学习的目的.解题活动不能是只求量不求质的刷题行为,解题一旦变成了简单的重复劳动,就意味着低效甚至无效.让我们的解题学习过程变得主动起来,让思维的运转更加活跃起来,才是提高思考和解决问题能力的有效途径.

