以长方体为模型的多面体外接球问题探究

魏东升

(福建省厦门双十中学漳州校区,福建 漳州 363107)

引例长方体的长、宽、高分别为3,2,1,其顶点都在球O的球面上,则球O的表面积为____.

该例实为2017年全国Ⅱ卷文科第15题,其实像这样直接考查长方体(或正方体)外接球的问题在高考中非常常见,解题的思路也并不复杂,主要是通过长方体的对角线即为其外接球的直径这一关系.可见借助长方体这一模型,对解决相关多面体外接球问题能带来很大的便利.究竟有哪些多面体可以补形成长方体呢?带着这个疑问笔者进行了以下探究:

(4)耕地、未利用地的变化与人口密度密切相关，林地受人均GDP影响最大，与建设用地最相关的因素是第三产业总产值。人口的增长必然会带来土地承载力的增加，经济的快速发展促使区域产业结构发生变化，第二、第三产业的发展加大了建设用地的需求。所以要进一步有效控制人口增长，完善对区域土地利用规划，实现土地利用结构的优化，使山东省的土地利用空间布局朝着合理、科学、有序的方向发展。

1 三棱锥

如果是从长方体8个顶点中选4个顶点,则可构成的几何体是以下几种特殊的三棱锥:

1.1 侧棱垂直直角底面

如图1,如果三棱锥的一条侧棱垂直底面,并且底面是一个直角三角形,则其可以通过补形成长方体来求解外接球问题.特别地,如图2,当垂足为底面直角顶点时,该三棱锥三条侧棱两两垂直.

图1 侧棱垂直直角底面图 图2 垂足为底面直角顶点图

例1 (2019年全国Ⅰ卷理12)已知三棱锥P-ABC的四个顶点在球O的球面上,PA=PB=PC,ΔABC是边长为2的正三角形,E,F分别是PA,AB的中点,∠CEF=90°,则球O的体积为( ).

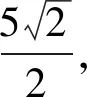
图3 2019年全国Ⅰ卷理12图 图4 两直角三角形共斜边图

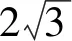
所以EF⊥平面PAC.

氟桂利嗪是临床中较为常用的一种双苯酰胺类钙离子拮抗剂，其对脑血管具有较高的选择性，在进入机体后，能够通过调节机体细胞内的钙水平降低患者的细胞钙失衡所带来的影响，同时其对于钙通道也具有较好的拮抗作用[2-3]。

从而PB⊥平面PAC.

速冻。保证冷冻食品食物感觉处于良好状态极为重要，为实现该目标，在冷冻食品时主要可以应用两种方法：一种为快速冻结，另一种为深度冻结。同时严格控制冻结温度，使其位于-35℃-45℃。设定一定时间限制，通常为30秒，使中心温度上升到-18℃。

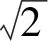
通过对项目的“打包”和“抓包”，地方政府既能将多项常规工作纳入到运动式治理的项目框架内，完成上级政府的指令和要求，又能够从上级部门获得各种资金支持。地方政府可以将这些项目和资金投到对自己的政绩和形象提升帮助最大的村庄，在投放(实际上是转发)过程中，能够通过对投放对象的取舍达成对村庄的控制。

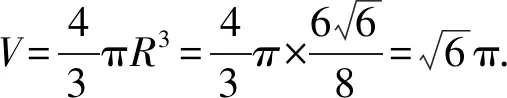
故选D.

1.2 两直角三角形共斜边

综上所述，通过种子贮藏技术的概念可以认识到种子贮藏技术是需要将多种因素相结合，然后针对不同农作物种子贮藏性能的不同进行相应的贮藏管理措施。当然最重要的还是要结合当地气候生态环境的不同，采取更加合理的种子贮藏技术。当然这还需要相关的人员进行深入的探究才能更好的实现对种子良好的贮藏。

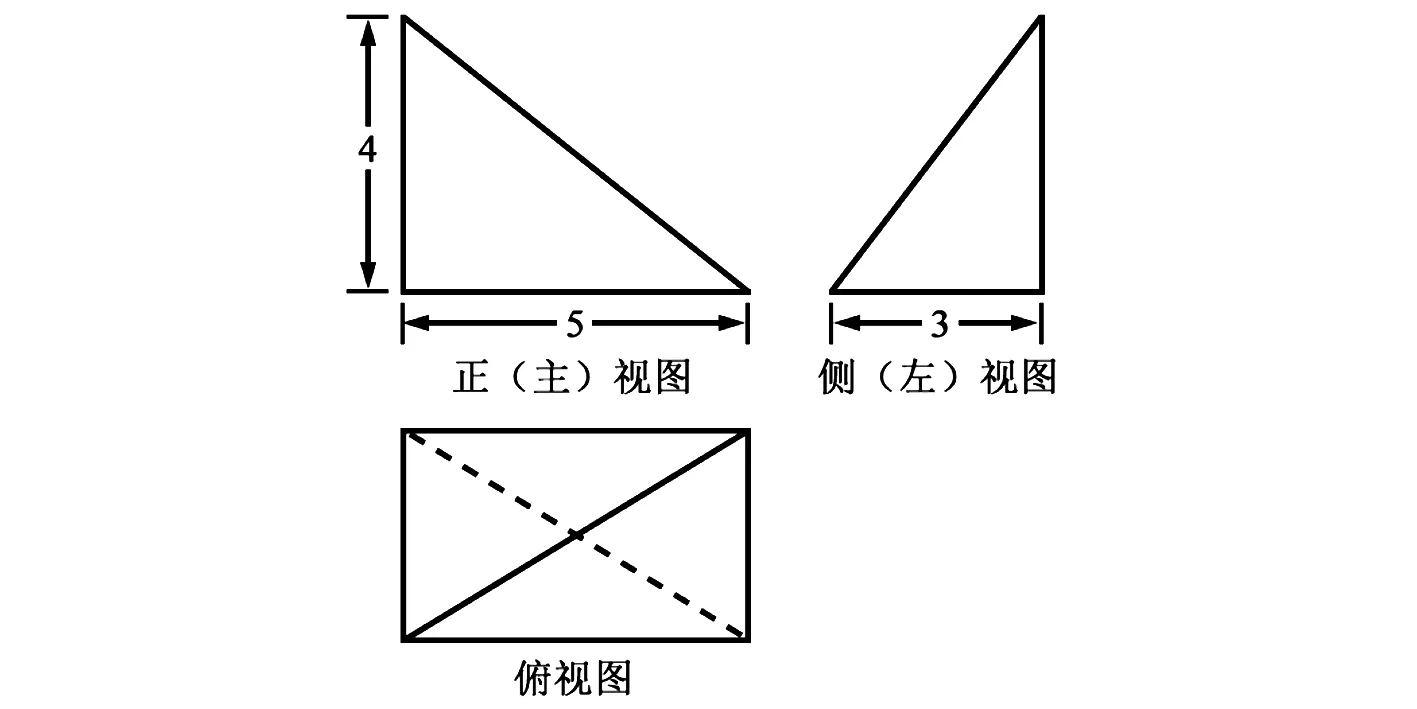
图5 2017年北京卷文6改编图

解析如图3,依题意P-ABC为正三棱锥,PB⊥AC,又E,F分别为PA,AB的中点,所以EF∥PB,EF⊥AC.

1.3 对棱相等

如图6,如果三棱锥的每组对棱的长度都相等,则其可以通过补形成长方体来求解外接球问题.

图6 对棱相等图 图7 2006年山东卷理12图

例3 (2006年山东卷理12)如图7,在等腰梯形ABCD中,AB=2DC=2,∠DAB=60°,E为AB的中点,将ΔADE与ΔBEC分别沿ED,EC向上折起,使A,B重合于点P,则三棱锥P-DCE的外接球的体积为( ).

对心脏彩超求得的TGI指数为:≥51岁TGI=288,男性TGI=138,已婚TGI=108。可知年龄最大的一组对心脏彩超的偏好性最强,且远超其它年龄段,男性比女性对心脏彩超的偏好性强。

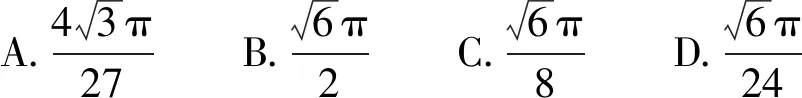
如图4,如果三棱锥的两个直角侧面有公共斜边,并且底面是一个直角三角形,则其可以通过补形成长方体来求解外接球问题[1].

关于翻译的研究，从“信、达、雅”到后来的“三美”理论，都有他们的必要性。但是总的来说，不论是什么作品的翻译，都不仅仅需要传达字面的意思，还应该根据不同国家的文化背景做适当的调整。对于英文电影字幕翻译，有它自己的特色。字幕是为了让观影者了解电影情节，有文化交际的功能。与此同时，字幕翻译的语言一般比较大众化，在逻辑性与艺术性等方面有着特殊的要求。

2 四棱锥

如果是从长方体8个顶点中选5个顶点,则可构成的几何体是以下两种特殊的四棱锥.

2.1 侧棱垂直长方形底面

如图8,如果四棱锥的一条侧棱垂直底面,并且底面是一个长方形,则其可以通过补形成长方体来求解外接球问题[2].

图8 侧棱垂直长方形 图9 直角三角形侧面垂直 底面图 长方形底面图

又因为EF⊥CE,CE∩AC=C,

对于音标教学，现如今人教版英语教材的编排是十分科学合理的，但是作为一名一线教师特别是农村英语教师却在教学实践中遇到如何把控音标教学“度”的困惑。

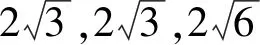
例2 (2017年北京卷文6改编)某三棱锥的三视图如图5所示,则该三棱锥外接球的表面积为( ).

2.2 直角三角形侧面垂直长方形底面

如图9,如果四棱锥有一个直角三角形侧面垂直底面,并且底面是一个长方形,则其可以通过补形成长方体来求解外接球问题.

例5 (2018年天津卷文11改编)如图10,已知正方体ABCD-A1B1C1D1的棱长为1,则四棱锥A1-BB1D1D外接球的表面积为____.

加快储气能力相关政策的落地。从目前来看，完成2020年“供气企业10%、城镇燃气企业5%、地方日均3天”的储气能力目标的难度较大，部分城镇燃气企业对政策理解不到位，仍处于观望状态。建议进一步出台更为具体的配套支持措施和考核办法，例如提供储气能力建设补贴资金；同时尽快理顺价格机制，加快促进调峰市场化运作，逐步建立储气库调峰服务市场。

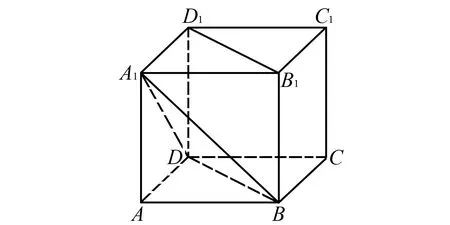
图10 2018年天津卷文11改编图

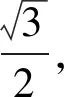
3 三棱柱

如果是从长方体8个顶点中选6个顶点,则可构成的三棱柱只有一种.如图11,如果三棱锥是一个直三棱锥,并且底面是一个直角三角形,则其可以通过补形成长方体来求解外接球问题.

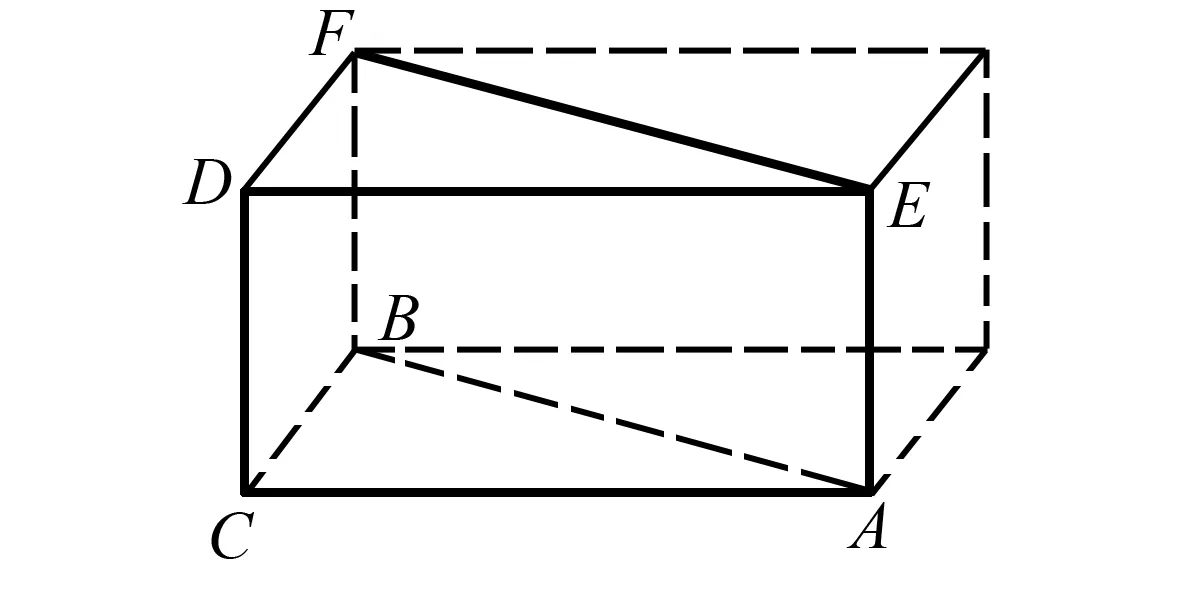
图11 三棱柱图

例6 (2013年辽宁卷文10理10)已知三棱柱ABC-A1B1C1的6个顶点都在球O的球面上,若AB=3,AC=4,AB⊥AC,AA1=12,则球O的半径为( ).

4 其他

以上几种类型是大家比较熟悉的多面体,在高考中出现的频率也比较高.借助分类思想,我们发现从长方体8个顶点中选5个顶点构成的多面体其实还有图12,选6个顶点还有图13、图14两种,如果选7个顶点则还有图15这种.其实,这些类型除了常见于外接球问题中,还常出现在三视图问题中,甚至是成为大题的考查背景.

图12 选5个顶点构成的多面体图 图13 选6个顶点构成的多面体图

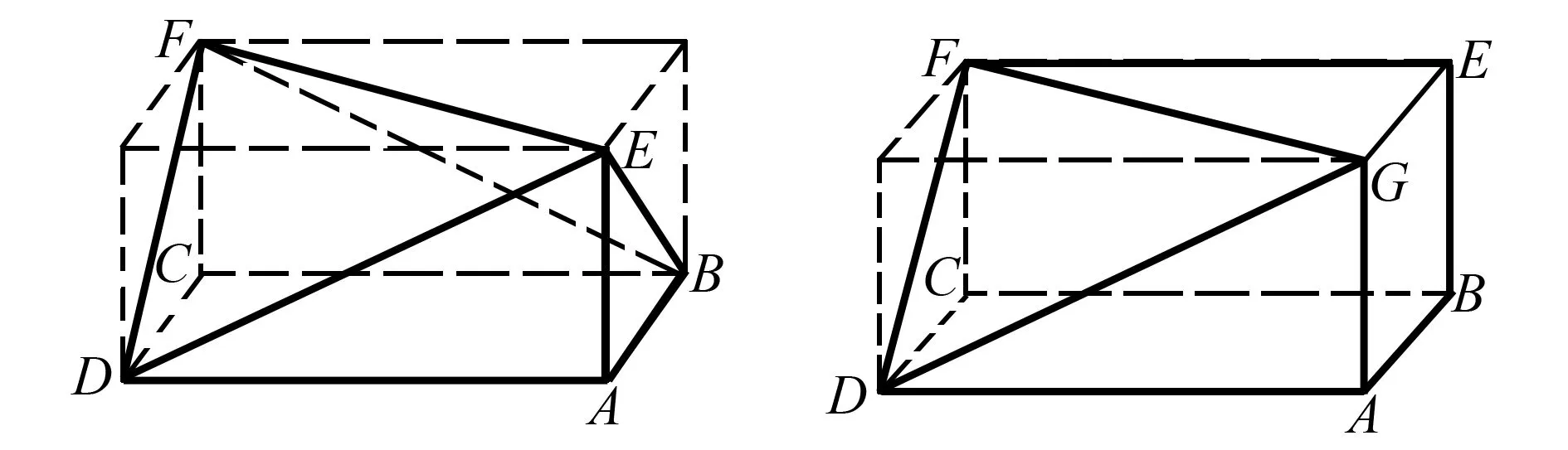
图14 选6个顶点构成的多面体图 图15 选7个顶点构成的多面体图