洞析教材内涵 把握高考题实质——以两道立体几何高考题为例

俞新龙

(绍兴市柯桥区越崎中学,浙江 绍兴 312050)

部分高考题源于教材、高于教材已经形成一种共识,但大多数认识仅停留在认为是课本题的改编或变式或引申等,实际上这样的认识是不够的,我们也应该对教材中的概念、定理、公式等引起足够重视,很有必要像研究语文段落一样,来讨论、研究它们的内涵与外延,并采用类比思维方式,从更广的范围来思考、探讨相关知识点或方法的可行性,从而更好地来指导、帮助学生数学解题[1].本文以数学教材立体几何中线面角、面面角的定义为例,结合2020年和2021年高考题来谈谈对该认识的研究,旨在抛砖引玉,引起大家的共鸣.

1 两道高考题及解答

题1(2020年全国新高考Ⅰ卷)如图1,四棱锥P-ABCD的底面为正方形,PD⊥底面ABCD.设平面PAD与平面PBC的交线为l.

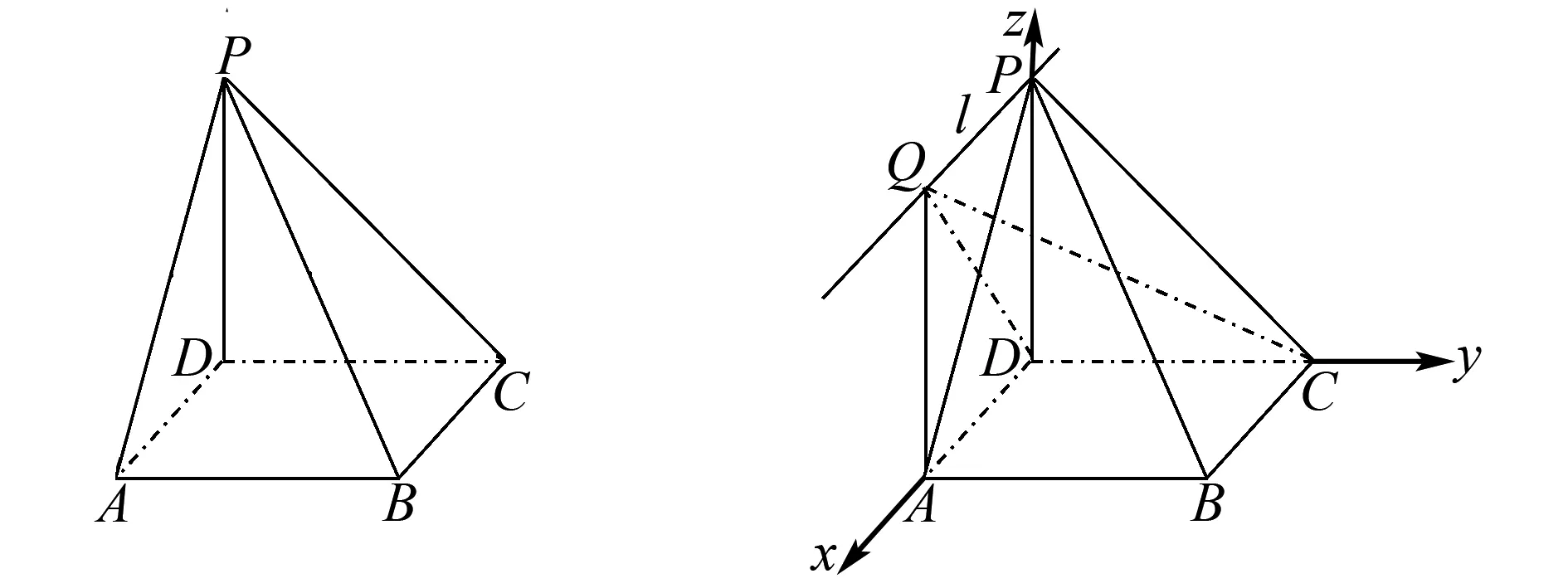
图1 题1图 图2 题1解析图

(1)证明:l⊥平面PDC;

(2)已知PD=AD=1,Q为l上的点,求PB与平面QCD所成角的正弦值的最大值.

解析(1)因为AD∥BC,AD⊂平面PAD,所以BC∥平面PAD,由线面平行性质知l∥BC.

因为PD⊥BC,CD⊥BC,PD∩CD=D,

所以BC⊥平面PDC.

所以,l⊥平面PDC.

(2)如图2建立空间直角坐标系,则D(0,0,0),C(0,1,0),B(1,1,0),P(0,0,1).

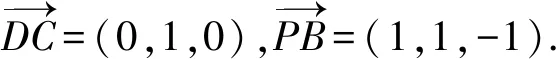
设平面QCD法向量为n=(x,y,z),则

可取n=(-1,0,m).

设PB与平面QCD所成角为θ,

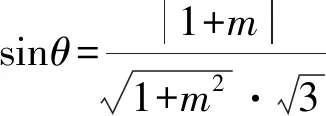
当且仅当m=1时取等号.

题2(2021年全国甲卷)如图3,已知直三棱柱ABC-A1B1C1中,侧面AA1B1B为正方形,AB=BC=2,E,F分别为AC和CC1的中点,D为棱A1B1上的点,BF⊥A1B1.

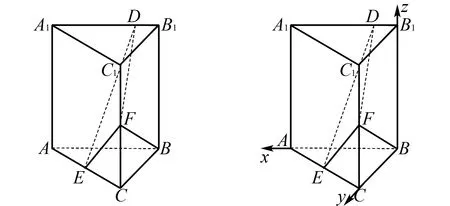
图3 题2图 图4 题2解析图

(1)证明:BF⊥DE;

(2)当B1D为何值时,面BB1C1C与面DFE所成的二面角的正弦值最小?

解析(1)由AB∥A1B1,BF⊥A1B1知AB⊥BF.

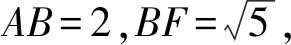
在Rt△ACF中,AC2=AF2-FC2=8,

所以A1E2=6,EF2=3,A1F2=9.

由勾股定理知A1E⊥EF.

又由面面垂直性质知BE⊥面AA1C1C.

所以A1E⊥BE.

于是A1E⊥面BEF.

所以可得A1E⊥BF.

又已知BF⊥A1B1,故BF⊥面A1B1E.

而DE⊂面A1B1E,所以BF⊥DE.

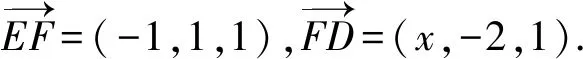
于是可取平面DFE法向量为n=(3,x+1,2-x),于是得

2 洞析教材内涵

以上两高考题考查的是线面角、面面角有关最值,题材相似,但却不落窠臼,考出了新意,具有一定的综合性.因为具有比较好的空间直角坐标系结构,所以绝大多数都会选择向量坐标方法求解,鲜有常规几何法求解,这就造成了一种错觉:常规几何法无法求解前述两高考题,或者说这样就掩盖了常规几何法的精妙,这是由于对教材中相关知识点理解不到位、不深入造成的.

2.1 教材中线面角、面面角的定义

(人教A版必修第二册151页)如图5,一条直线l与一个平面α相交,但不与这个平面垂直,这条直线叫做这个平面的斜线,斜线和平面的交点A叫做斜足.过斜线上斜足以外的一点P向平面α引垂线PO,过垂足O和斜足A的直线AO叫做斜线在这个平面上的射影.平面的一条斜线和它在平面上的射影所成的角,叫做这条直线和这个平面所成的角.

图5 线面角定义图 图6 二面角的平面角定义图

(人教A版必修第二册156页)如图6,在二面角α-l-β的棱l上任取一点O,以点O为垂足,在半平面α和β内分别作垂直于棱l的射线OA和OB,则射线OA和OB构成的∠AOB叫做二面角的平面角.

2.2 定义分析,洞析内涵

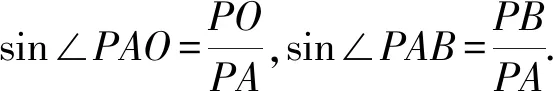
(2)如图7,若另有一包含直线AB的平面β,若PO1⊥β,作O1B1⊥AB1,所以∠PAO1<∠PAB.这就告诉我们,∠PAB比直线l与经过直线AB的任意平面所成的角都要大;进一步可以知道,若另有一条平行于直线AB且与直线l异面的直线CD,则异面直线l与CD所成的角是直线l与经过CD的任意平面所成角的最大角.

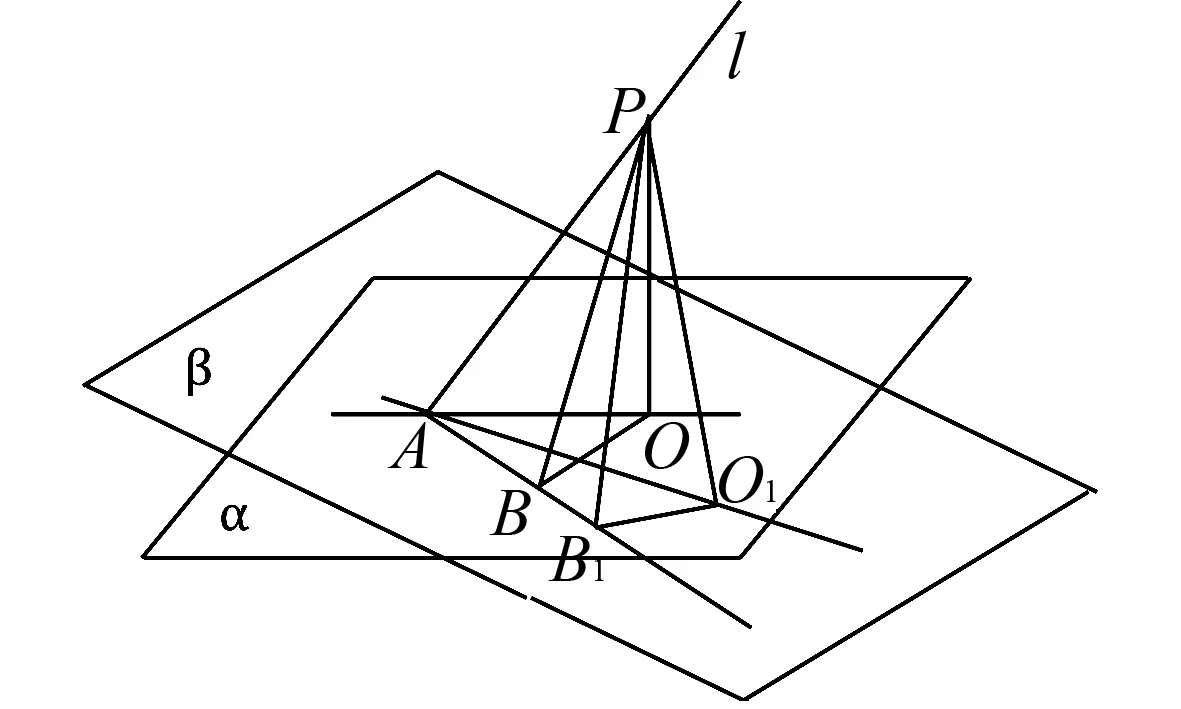
图7 线面角内涵图

面面角内涵分析根据这个描述性作法可知平面角不仅唯一而且还是两个半平面α和β内任意各一条直线所成角中最大的角(若另有CA和CB构成∠ACB,则由初中知识就能知∠AOB>∠ACB).因此,二面角的平面角应该大于等于其中任何一个半平面中任意一条直线与另一个半平面所成的角[2].

3 把握高考题实质

理解清楚这些后,我们再回到高考题来找寻“神奇”的常规几何解法.

图8 题1的线面角图

图9 题2的线面角

又因为EF⊂面DFE,且EF位置具有固定不变的特点,所以面BB1C1C与面DFE所成的平面角大于等于EF与平面BB1C1C所成的角,因此问题便成为了是否存在点D,使得∠EFG就是面BB1C1C与面DFE所成的平面角.

如图9,因为A1A,FE共面且不平行,所以A1A,FE必相交于一点A2,且AA2=1,同样地,A2D,BB1共面且不平行,所以A2D,BB1必相交于一点P,连接PF,又因为P∈面DFE,P∈面BB1C1C,所以PF是面BB1C1C与面DFE的公共棱.

因为EG⊥PF,所以当FG⊥PF时必有EF⊥PF(或者EF⊥PF时必有FG⊥PF),此时∠EFG就是面BB1C1C与面DFE所成的平面角.下面通过FG⊥PF来确定点P的具体位置,从而再确定点D位置[3].

在Rt△FCG中,FG2=2,在Rt△PBG中,PG2=1+(2+B1P)2,在Rt△PSF中,PF2=4+(1+B1P)2,在Rt△PFG中,PG2=FG2+PF2,解得B1P=1.

4 教学启示

高考题以解答对得满分为原则,但教学却应该以学生数学核心素养发展为目的.回顾两立体几何高考题常规方法的解答过程,无疑给我们数学教学带来一些启示.

4.1 研读数学教材永远都不过时

数学教材是师生学习数学知识的蓝本,大多数知识都是显性呈现的,但也有相当一部分知识是隐性呈现的,需要师生一起去努力挖掘找出来,虽然说“师傅领进门,修行靠自身”,但数学教师的引领和示范作用绝对是不能缺失的,因为“一个专心备课的教师能够拿出一个有意义的但又不复杂的题目,去帮助学生挖掘问题的各个方面,使得通过这道题,就好像通过一道门户,把学生引入一个完整的理论领域”(波利亚).上述两高考题的命题者连续两年提醒教师,要重视教材知识发生的核心要义,即知识的内涵与外延,这就要求我们在平时的教学中,要通过同伴互助、教研组协作、专家引领等各种方式认真研读数学教材.

4.2 数学学习需要跳出题海研究问题的规律性

茫茫题海扼杀了一大批优秀学生的数学创新思维发展,使他们缺少了用自己独特的解题眼光去解题的机会,十分不利于数学核心素养的获得.对同一个数学问题,不同水平的学生会有不同的解题方法,最好的方法肯定是明了问题本质、掌握问题规律的独特方法,但现在学生囿于刷题,无暇思考,缺少了探究问题间存在联系的能力,也就缺少了发现问题背后所隐藏某种规律的机会.数学的最大魅力就是变化之中往往含有不变性,这才应该是师生着重探究的.