线段图在小学行程应用题教学中的应用

周建中

【摘要】行程应用题是小学数学的重点与难点，学生在求解这类问题时往往会不知如何入手.一来行程问题本身涉及了时间、速度与路程三个量，二来行进的过程本身可能比较复杂，比如追及问题等，学生如果没有理清其中的关系，就无法列式进行计算.文章首先分析了线段图在行程应用题教学中的作用，然后列举了常见的行程应用题，旨在通过线段图来分析行程问题，把复杂的问题简单化与直观化，提高学生解题效率.

【关键词】线段图；行程问题；解题应用

引 言

行程应用题是小学高年级数学的学习难点，问题种类比较多，有一般的相遇、追及问题，还有流水行船问题，等等.不少学生都依赖于公式来求解，如果情况一旦变得复杂，或者问题的背景不那么直观，学生就很难理清题目中各个量之间的关系，无法正确求解.下面笔者借助线段图来分析行程问题，通过线段图把行程问题所涉及的时间、速度与路程三个量形象化、直观化，理清在问题的各个阶段中三者之间的关系，从而求解问题.

一、线段图在小学行程应用题教学中的作用

（一）帮助学生理解题意

在解决行程问题时，学生常常会遇到文字描述较为抽象、信息量大且关系复杂的情况，这使得他们难以快速理清题意.而线段图作为一种直观的教学工具，能够通过图形的方式展示题目中的信息，将抽象的文字描述变得生动具体，帮助学生更好地理解题意.例如，在相遇问题中，学生常常需要理解两个物体在某一时间段内的相对位置和运动关系.如果仅仅通过文字描述，学生可能会感到困惑，难以清晰地想象出物体的运动轨迹和相对位置.而通过绘制线段图，学生可以将题目中的信息以图形的方式呈现出来，更加直观地了解物体的起始位置、运动方向和速度等关键信息.这样一来，学生就能够更好地理解题目的本质，清晰地看出数量关系，从而快速找到解题方法.

（二）简化复杂问题

在解决复杂的行程问题时，学生常常会面临大量的文字信息和复杂的数量关系.这些信息如果仅通过文字描述或口头讲解，学生可能会感到困惑，难以把握问题的核心.而线段图能够清晰地表示出数量关系，将复杂的文字描述简化为简单的图形表示.通过绘制线段图，学生可以对题目中的各种信息进行整合和简化，将复杂的文字描述转化为直观的图形.这样，学生可以更加清晰地看到各个量之间的关系，避免出现在大量文字中迷失方向的情况.同时，线段图的使用也降低了学生的认知负荷，使得问题变得更加容易解决.

（三）培养学生的逻辑思维和空间想象能力

在解决行程问题时，学生需要具备一定的逻辑思维和空间想象能力来理解物体的运动轨迹和相对位置.通过绘制线段图，学生需要将文字描述转化为图形，并从中找出数量关系.这一过程需要学生具备一定的逻辑思维，对问题进行有条理的分析和推理.首先，学生需要根据题目的描述，将文字信息转化为图形元素.这需要学生具备一定的空间想象能力，能够准确地想象出物体的运动轨迹和相对位置.通过绘制线段图，学生能够更加直观地看到各个量之间的关系，从而更好地理解题目的本质.其次，在解决行程问题时，学生还需要具备一定的逻辑思维.他们需要根据线段图中的信息，分析各个量之间的关系，找出解题的关键.这需要学生具备对问题的分析和推理能力，能够从线段图中提取关键信息，并进行逻辑推理.通过训练，学生可以逐渐提高自己的逻辑思维和空间想象能力.他们可以更加熟练地绘制线段图，更加准确地分析各个量之间的关系，从而更加高效地解决行程问题.

二、常见行程应用题举例

行程应用题是小学阶段数学应用题的重要类型之一，对于培养学生的逻辑思维和问题解决能力具有重要意义.然而，由于行程应用题涉及的概念和关系较为复杂，许多学生在解决这类问题时感到困难.线段图作为一种直观的图形表示方法，能够帮助学生更好地理解题意，找出数量关系，从而提高解决行程应用题的能力.下面用具体的例子来展示线段图在解决行程应用题中的重要作用.

（一）相遇、追及问题

例1 A，B两地之间的路程为726千米，甲、乙两车分别从两地同时开出，匀速相向而行，甲车平均每小时行驶22千米，乙车速度比甲车速度快11千米，行驶多久两车之间还相距121千米？

思路分析 行程问题涉及的基本量为速度、时间与距离，为此需要把题目所给的条件作适当的转化.先算出乙车的速度为22+11=33（千米/时）；整个行程可以用图1表示.显然该问题是对常规的相遇问题做了一定改变，但从线段图上看，还是具有相遇问题的特点：两车相向而行，经过多长时间两车距离为121千米.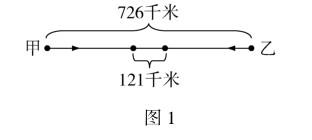

解题分析 从图1中可以发现，此问题就是一个普通的相遇问题，只要把两地的距离修改为726-121=605（千米），用两地距离除以两车行进速度和即可得到最终答案.此时两车相遇所用的时间为：605÷（22+33）=11（小时），即两车经过11小时后相距121千米.利用线段图可以很容易地表示出甲、乙两车的距離，并且这里借助箭头表示出甲、乙两车的行驶方向，也可以表示速度的大小.这样就可以把行程问题的两个因素在同一张图中表示出来，这样不仅可以把复杂、抽象的行程问题通过线段直观地表示出来，而且可以简化问题的条件，把条件集中到一起，这样更加有利于对问题的分析与求解.

例2 公交车每天都从始发站发车，假设每次发车的时间间隔均相同，每辆车都以固定的速度匀速行驶在公路上，忽略停车、上人需要的时间.路人甲匀速走在行车路线旁边的人行道上，他发现一个规律，就是公交车迎面和背面驶来的时间间隔是6分钟和12分钟，求始发站每隔多少分钟发一趟车.

思路分析 问题的背景学生都很熟悉，只是增加了一些理想化的条件，所以让学生理解本题是没有问题的.只是题目所给的条件太少，在路程、速度与时间三个要素中，只是给出了时间一个要素，并且整个行程也比较复杂，常识告诉我们会有多辆公交车在线路上运行，整个公交运行线路的长度未知，运行速度也未知，不仅如此人的行走速度也未知.总之，题目所给条件太少，且行程较复杂.

解题分析 对于这类条件明显较少问题的求解，通常的一个思路就是，在题目所给条件没有出错的情况下，所求的结论与未给的条件之间是不存在关系的.就如本题而言，公交车的发车间隔、公交车的运行速度、人的行走速度，与公交运行线路的距离之间是没有依赖关系的，这点会使大部分学生感到意外.所以，求解此类问题的关键在于仔细分析整个行程过程，不能忽略每一个细节.而分析问题的根据就在于行程问题的基本关系式：路程=速度×时间.为了分析问题方便，用v1，v2分别表示公交车与人的速度.根据题意，公交车在始发站是等间隔发车，并且不考虑在各个站点的停留时间，所以在整个公交车的运行线路上，前后两辆公交车之间的距离总是定值，这里不妨将其设为L.这个距离对于本题的求解至关重要.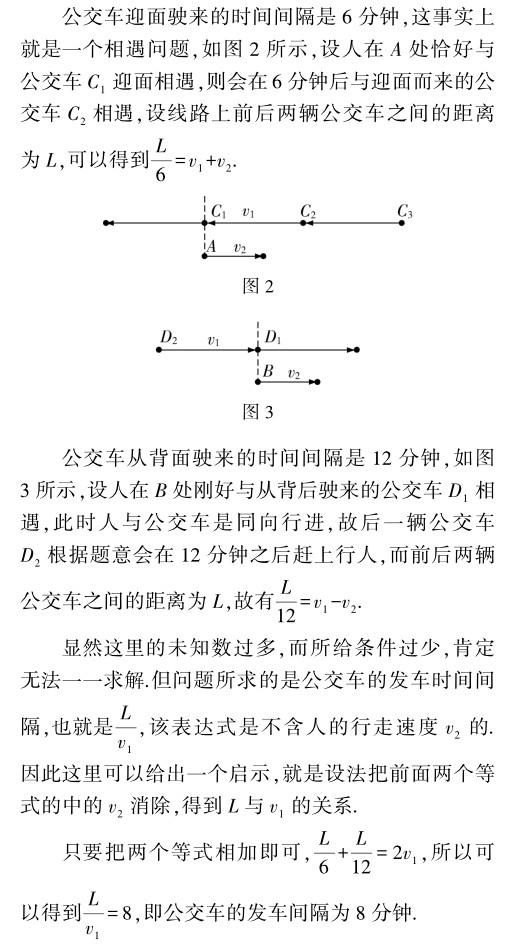

本题的求解带有明显的代数思维方式，在这里也可以把相邻两辆公交车之间的距离作为单位“1”进行求解，如下所示.

将两种求解方法进行对比可以发现，后一种解法更加具体一点、小学生更加容易接受一点.只是把两车的距离设置为单位“1”时，会有学生弄不明白.在这一点上第一种解法更好理解一点.第一种解法对学生有着更高的要求，需要学生具备一定的逻辑推理能力及代数式的恒等变形能力.

（二）流水行船问题

另一种常见且复杂的行程问题则是流水行船问题，问题的背景都是日常生活中经常遇到的情况，显然船在顺水中行驶，其速度要比在静水中快；反之在逆水中行驶，速度要比在静水中慢，而这增加的速度或者减少的速度，正是水流的速度.这正是流水行船问题的基本原理.

例3 一艘小船从甲地开往乙地，此时小船是顺水而行，小船的速度是28千米/时，小船到达乙地后逆水驶回甲地，小船再次回到甲地时，发现回来比去时多行驶了2个小时，已知水流速度是每小时4千米.甲、乙两地相距多少千米？

思路分析 流水行船问题涉及的量相对较多，首先要确定两个基本量，一个是水流速度，这里题目已经给出是4千米/时；另一个为小船在静水中的速度：28-4=24（千米/时），从而可以得到船在逆水中行驶的速度：24-4=20（千米/时）.从图6中可以发现回程时多行驶的2小时，正是由去程与返程时的速度差28-20=8（千米/时）造成的.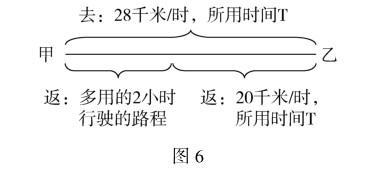

解题分析 小船在静水中的速度為28-4=24（千米/时），小船逆水行驶的速度为24-4=20（千米/时），返程多用的2小时行驶的路程为2×20=40（千米），而这40千米正是由往返时的速度差即：28-20=8千米/时所造成的.所以去的时候总共所用时间为40÷8=5小时（即小船从甲地到乙地所用时间为5小时），故两地距离为28×5=140（千米）.

结 语

综上所述，线段图作为一种直观的图形表示方法，能够将抽象的文字描述转化为具体的图形表示，帮助学生更好地理解题意.同时，通过线段图的绘制和应用，学生能够逐渐掌握解决行程应用题的思路和方法，提高问题解决能力.在实际教学中，教师需要注意根据学生的实际情况和个体差异进行有针对性的指导，以帮助学生掌握解决行程应用题的思路和方法.

【参考文献】

[1]王琳.“微时代”应用于行程问题中的优势[J].天津教育，2019（30）：60-61.

[2]卞慧.小学数学行程问题的解题思路[J].小学生（上旬刊），2022（2）：58-60.

[3]陈燕.多角度切入推动小学数学行程问题教学[J].小学生（上旬刊），2022（2）：13-15.

[4]叶润霞.线段图在小学数学应用题教学中的运用策略研究[J].数学学习与研究，2022（6）：89-91.