基于思维进阶的小学数学习题设计与开发策略研究

徐慧琴

【摘要】数学习题具有渐进性、实用性特点，开展习题设计与开发，有利于学生通过解题牢固掌握数学知识、技能.习题设计与开发是小学数学教师的重要教学工作，能培养学生的数学思维能力和应用能力.文章结合实际习题案例，总结了基于思维进阶的习题设计与开发策略，旨在为教师的习题研究提供思路，促进学生思维与解题能力的发展.

【关键词】小学数学；思维进阶；习题设计；教学策略

习题设计与开发，能满足学生在不同阶段的数学学习需求，对于学生的思维进阶大有裨益.高质量的习题能激发兴趣、开发智力、拓展思维.当前习题设计中存在机械性、重复性问题，不利于提升学生的思维品质.教师需要改变墨守成规式的习题设计思路，运用科学方法开发习题资源，推动学生思维进阶，同时树立全新的习题观、学生观，敢于打破常规，设计指向思维进阶的数学习题，培养学生良好的思维能力.

一、“一題”至“多题”———在习题变化中提升学生思维灵活性

灵活多变的思维，是学生创新发展的基础.在习题设计中，教师应关注学生的创新思维发展，利用“一题”至“多题”的过渡，让学生在解题中融入个人的思考与理解.教师可以鼓励学生创造性地解题，探究解决同一问题的多种方法，使其能在解决习题过程中，提升自己思维的灵活性.

以“长方体和正方体”一课为例，教师应挖掘教材习题中的隐性知识结构，立足创新思维的培养，设计多样性习题.在习题设计中，教师应聚焦对学生的观察、比较、分析等能力的培养，寻找思维聚力点，利用习题提升学生思维的灵活性，让学生深刻理解知识，使其思维向纵深发展.

【习题设计】

例1 已知正方体（如图1）可以被平均分成两个同样的长方体，若正方体的棱长为6厘米，那么两个长方体的表面积之和比正方体增加了多少？

设计分析 参考图例可知，两个被分割出来的长方体表面积之和比正方体表面积有所增加，所增加的恰好为正方体两个面的面积之和.通过解题，学生可以初步建立有关知识的表象，理清相关概念关系.教师可以在例1的基础上进行创新.

例2 将一个正方体平均分，得到两个表面积相同的长方体，已知一个长方体的表面积为144平方厘米，请求出正方体的表面积.

设计分析 在“例1”的基础上，教师将问题条件顺序进行置换，改变问法，可以引导学生从不同的角度进行思考、分析.学生聚焦“两个长方体的表面积之和”，能比较正方体表面积与两个长方体表面积之和，从多个角度分析问题条件，运用所学公式进行求解，懂得运用不同的方法进行解题.

解题过程 （第一种方法）144÷（1×2+0.5×4）=36（平方厘米），36×6=216（平方厘米）.

（第二种方法）2×144÷（6+2）=36（平方厘米），36×6=216（平方厘米）.

在创新例1的基础上，学生能从不同的角度思考，对两道题进行求解.由“一题”至“多题”的演变，使学生能感受到数学学习的整体性，进而在原有数学知识的生长点上，依托长方体和正方体表面积公式进行求解.结合题意可知，长方体表面积是原正方体4个面的面积之和.“例2”在“例1”的基础上进行了延伸，另辟蹊径，充分、巧妙地转化了矛盾点，让学生能感受同一问题的不同问法.教师巧妙利用多道习题刷新学生对同一题型的认知，使他们能在问题条件的纵向比较中，整体理解“两个长方体表面积之和”与“正方体表面积”的关系，在积累审题经验的同时，感知几何信息的表象，全方位运用所学概念分析解题思路.“多题”习题设计凸显了教师培养学生创新思维的理念，能让学生在思考中产生新的解题思路，提升学生的思维灵活性，助力学生思维进阶.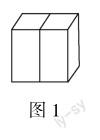

二、“新题”至“旧题”———新旧关联中提升学生思维的系统性

全新的习题能给学生带来耳目一新之感，激发他们的解题兴趣，使其获得内部学习动机.基于思维进阶的习题设计与开发，需要立足学生的系统化思维发展，即对旧的习题进行改编，链接学生已经学过的数学知识，从知识系统化的角度入手，编创习题，以实现“新题”至“旧题”的过渡.在解决“新题”时，学生能精确、综合分析，认识和理解所学数学重难点知识，在原有知识框架中，进一步完善数学知识体系.

以“圆”一课为例，教师可以引导学生运用所学知识解决问题，在习题设计中，将学生学习过的知识与新知识建立起联系，让学生在解题过程中强化代数推理、几何想象能力.

【习题设计】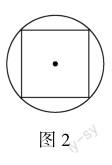

例3 如图2，圆的中间有一个正方形，正方形的面积是10平方厘米，请求出圆的面积.

设计分析 此题可以先求圆半径的平方，再计算圆的面积.在解题过程中，学生通过用字母代替半径，回忆学习过的正方形面积知识，初步尝试用字母解决问题，运用学过的知识寻找有助于解题的条件，推动新旧知识的迁移.

部分学生对“用字母表示数字”的理解流于表面，在后续的圆的知识学习中，难以合理运用.针对这种情况，教师可以对习题进行创新，基于真实学情，在原有习题基础上进行变化，将新旧数学知识联系起来，启迪学生的系统思维.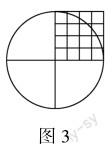

例4 以正方形的边长为半径画一个圆（如图3），请用数方格的方法，计算出圆的面积（每一小格的面积为1平方厘米）.

设计分析 通过“例4”与“例3”的比较可知，学生能在解题中理解圆的面积为圆半径平方的3倍多，即正方形面积的π倍就是圆的面积.本题设计遵循学生的新知识学习规律，将旧知识（数方格的方法）融入问题条件中，让学生能由表及里地分析问题条件，探索此类问题的解决方法.小正方形的边长就是圆的半径，圆的面积就是正方形面积的π倍.学生能由这一表象关联到一类问题中，从而获得解决问题的思路.

从“旧题”至“新题”的过渡，能让学生构建数学模型，先求出小正方形的面积，再根据数学模型，求解圆的面积.在此基础上，教师可以基于学生的思考，设计新题，引导学生进行深入研究，使其能探究数学知识本源，建立适配的数学模型，在解题中加深学习体会和感悟，提升思维的系统性.

三、“单题”至“题组”———在对比理解中提升学生思维的深刻性

学生的数学解题是由单一至具体，由直观到抽象的过程.教师应认识到学生思维在解题中的变化，利用“单题”至“题组”的过渡，让学生形成关于数学知识的深刻认知.在设计和开发习题时，教师有必要以课堂为载体，借助习题的延伸，促进学生理解知识内涵，使其思维深刻性得到提升.

以“分数除法”一课为例，教师可以通过习题训练，推动学生思维进阶，利用合理的习题“量变”促成思维进阶的“质变”，在“借题变题”中，助力学生思维进阶.

“分数除法”一课是在学生学会一个数除以整数的基础上进行的，相关习题的设计与开发顺应学生的认知发展规律，能让学生从一个数除以整数的计算方法，逐步迁移到一个数除以分数的方法中.教师根据同一例题设计延伸问题，不仅能让学生参考之前解题的思维结果，还能创设开放度较高的课堂探究环境，让学生保持积极的思维状态和宽松的学习探究气氛，进而在解题中提升思维的深刻性.

四、“方法”至“能力”———变式训练中提升学生思维综合性

学习方法的掌握会推动学生的思维进阶，从而提升其解决问题的能力.习题设计与开发可以从变式训练入手，以体现学生对知识的反思，逐步实现解题“方法”至“能力”的过渡目标，丰富课堂教学内容，提升学生思维综合性.

以“解决问题的策略”一课为例，本课重视引导学生运用转化思想方法解决问题.教师可以设计与实际生活有关的习题，通过变式训练，引导学生体验转化的方法及应用，丰富课堂教学内容，推动学生思维进阶.

【习题设计】

例6 已知一袋大米重75千克，一袋面粉重25千克，现有一辆载重为5吨的轻型卡车，已经装了40袋大米，还能装多少袋面粉？

习题分析 从条件入手分析，可知根据已装的大米袋数和每袋大米的重量，能算出车上大米的总重量，利用车的载重量减去车上大米的总重量，再除以每袋面粉的重量，问题便迎刃而解.

为了提升学生思维的综合性，教师可以从学生的生活出发，设计与“例6”相关的变式问题，加大对学生思维引领的力度，通过习题帮助学生实现由解题“方法”至“能力”的过渡目标.

例7 已知有两套不同的运动服，价格分别是130元、148元，有两顶不同的帽子，价格分别是16元、24元，有两双不同的运动鞋，价格分别是85元、108元.现有300元预算，想购买一套运动服、一顶帽子和一双运动鞋，预算够吗？最省钱的方案是什么？能剩下多少元？

习题分析 在变式训练中，这道题能让学生参考大量的已知条件，从中分析隐性条件.如果从条件出发向问题推理，不利于高效解题.所求问题是推理切入口，学生应该明确所求问题中蕴含的数量关系“剩下的钱=付出的钱-物品的总价”.确认条件后，根据“最省钱”这个词展开思考，便能提取已有经验，正确解题.

为了凸显变式训练从问题出发的特点，教师可以引导学生回顾解决问题的过程，紧紧抓住从问题向条件推理的解题思路特点，为学生提供其他的变式训练习题，从而做到“趁热打铁”，巩固学生对解题方法的理解，使其能掌握解决同类型习题的技巧，提升自己的解题能力.

結 语

综上所述，教师优化习题设计，开发多样化习题资源，能巩固和加深学生对重难点数学知识的理解，提高其思维能力与应用能力.教师以当前学生的思维状况为参考，聚焦思维进阶设计、开发习题，能提高习题资源与教学内容、学生学习需求的适配性，让学生在运用数学知识解决实际问题时，积累解题经验，取得学习进步.在今后的习题设计与开发中，教师应运用富有启发性的习题，激起学生的解题兴趣，将他们的思维引向深处，逐步运用习题推动学生的思维进阶发展.

【参考文献】

[1]张维维.“让学引思”理念下小学第一学段数学习题设计研究[J].教学管理与教育研究，2022，7（20）：91-92.

[2]郝瑞亚.主体间性理论视域下推动学生数学思维进阶的路径探索[J].江苏教育，2022（65）：52-55.

[3]沈淑阳.指向学力生长的小学数学习题设计策略研究[J].求知导刊，2022（18）：23-25.