教在学生的需求处

王玲玲

［摘 要］教学“平行四边形和梯形”时，通过前测了解学生的学习起点、痛点和生长点，为学生精心准备操作材料，引导学生动手操作，使学生能够亲身感受平行四边形和梯形的特征及它们的区别与联系，并迁移方法学习其他图形，从而深刻掌握平行四边形和梯形的有关知识，并发展知识迁移能力。

［关键词］学生需求；核心素养；平行四边形和梯形

［中图分类号］ G623.5［文献标识码］ A［文章编号］ 1007-9068（2023）32-0038-03

基于学生需求而教是实施教学的自然之道，能让学生听明白、有感触、有发展的课才是一堂好课。因此，教师应从学生学的角度创造性地使用教材，始终緊扣学生需求思考学生现在在哪里、未来要走向哪里、从现在到未来应该怎样走，从而让“学生需求”看得见、可操作。

下面，笔者以北师大版教材四年级下册“平行四边形和梯形的认识”为例，具体阐述自己的一些思考。

一、现在在哪里——学情调研，焕新学习生态

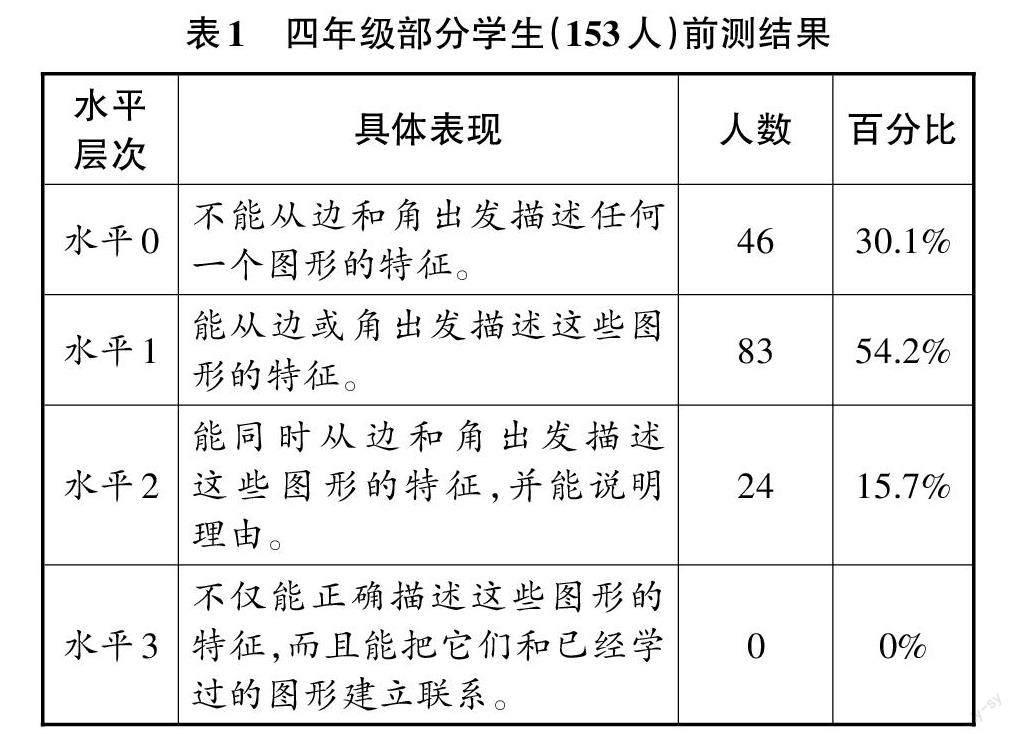
教师应充分了解学生的初始水平，这样才能更加科学地进行教学设计。为了了解学生的“学习起点”、“学习痛点”与“学习生长点”，笔者对四年级部分学生进行了前测（题略），结果见表1。

可以看出，这部分学生中多数人的几何思维水平处于水平0或水平1，对待需判断的对象是根据直观上“形状相同，像不像”来确认的。学生判断瘦长或摆放不正的平行四边形时错误率较高，对长方形、正方形与平行四边形之间的关系认知混乱，可见还没抓住图形的本质特征。

通过前测，笔者发现学生对平行四边形、梯形的学习已经不局限于课本知识，而是动态地生成了许多关于平行四边形、梯形的问题，包括“它们和以前学过的其他图形有什么联系？”“今天的图形认识与后续立体图形的认识在方法上有什么相同之处？”“平行四边形、梯形面积又是怎么计算的？”等。

二、未来走向哪里——以终为始，构建学习体系

1.构建知识图谱

在领域视角下，从平面图形到立体图形，最终指向的都是边、棱以及角这些要素的认识和关系的研究。一年级的认识图形是对所有平面图形的直观判断，到了三年级，学生就要对图形的特征从边和角的角度进行准确的数学描述。在后续的学习中，学生还需要对更多的图形进行特征描述和属性解释，建构图形之间的关联，从感性认识上升到理性认识。因此，这节课笔者的教学将从“认识要素”和“沟通关系”这两个维度入手。

2.提炼核心素养

培养空间观念既是“图形与几何”领域教学的一项根本任务，也是学生个体成长的必然要求。空间观念有助于学生发展观察力、实践力、想象力、表达力与推理能力。那么基于知识的序和学生的需，教学“认识平行四边形和梯形”时，教师该如何依据素养导向，整体建构图形认识，提升学生的核心素养呢？

首先通过分类链接学生关于平行线的经验，整体建构边的要素和基本特征；然后创设“造四边形”这一活动群，加深学生对图形本质特征和图形之间关系的理解；最后引导学生“动思结合”，拓宽学习视角，发展学生的直观想象能力、推理能力和空间观念。

三、应该怎么走——多维助力，丰富学习质感

1.精选材料，助推本质理解

如何让学生对图形的认识从模糊走向清晰？“儿童的智力在他的手指尖上。”在“图形与几何”领域的课堂中，教师可以让学生通过各种各样的操作活动体验知识的形成和发展过程，引导学生主动地发现知识， 感悟数学知识的来龙去脉。为避免学生的探索无序、盲目和低效，课堂上所呈现的探究材料、问题和数学学习方式均要体现数学结构， 兼顾数学知识的本质属性。例如，在“认识平行四边形和梯形”的教学中，笔者精心为学生准备了探究材料（见表2）。

这些材料关注的是不同的属性研究。利用这些材料进行操作后，学生会对平行四边形与梯形的图形本质特征有一个完整清晰的认识，为以后学习图形的面积以及探究立体图形打下基础。

2.活动赋能，实现自主建构

皮亚杰曾言：“空间观念的形成不像拍照，要想建立空间观念，必须有动手做的过程。这个做的过程，不仅是一个实践的过程，更是尝试、想象、推理、验证、思考的过程，只有在这样的过程中，儿童才能把握概念的本质，建立空间观念。”因此，教师在本节课中应通过创建丰富的、有进阶的活动群或活动链，让学生在动思结合的过程中领悟知识的本质与内涵，深度体验图形本质和图形之间的关联，建立和发展良好的空间观念，从而实现自主建构。

【案例】执教“认识平行四边形和梯形”操作活动课堂实录

活动一：摆一摆——借平行线造四边形

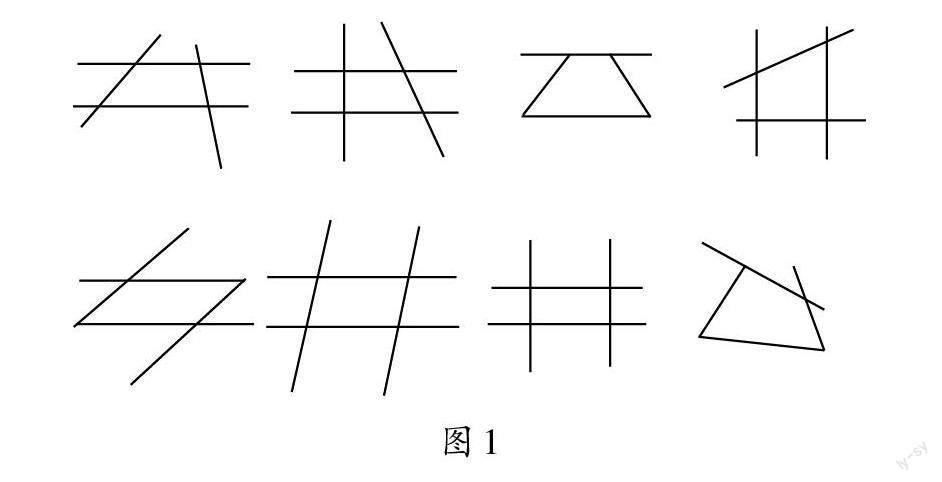
师（出示图1）：观察摆好的图形，梯形在哪里？平行四边形呢？

活动二：找一找——特殊的四边形

师：这节课我们来认识特殊的梯形。

师：在摆好的作品上移一移小棒，感受平行四边形、长方形和正方形之间的关系。

活动三：造一造——关注图形的分与合

师：你还能通过什么方式创造出梯形或平行四边形？

生1：沿着与三角形的一条边平行的直线剪一刀，可以得到一个梯形。

生2：两个完全相同的三角形可以拼成一个平行四边形（如图2）。

生3：可以用不同的材料、不同的方法、不同的图形构造平行四边形和梯形（如图3），它们之间是有联系的。

通过这样连续的活动，学生经历了“找平行线—从形上感知、构造四边形—理解本质特征—观察运动中的四边形—感受四边形之间的关系”的过程。在“立—破—立”中，学生首先从静态学习走向动态学习，不断体会图形的边和角之间的关系，感受其内涵的丰富性，深悟图形的本质；接着教师帮助学生链接思维，从手动走向脑动，让学生在丰富的活动中不断复盘与反思，在“变与不变”中不断感受边和角的变化引起的图形变化，感受不同四边形之间的关系。

3.整体关联，推进学法迁移

在单元整体的背景下，教师应注重知识之间的内在结构和关联，让学生不断感受到数学课上所学习的方法是有再生力和牵引力的，可以帮助自己学习和认识更多的图形。教师还要帮助学生迁移学法，使学生感受到整个“图形与几何”领域学习方法的一致性，掌握认识图形的通法。

【案例】执教“认识平行四边形和梯形”一课的整体关联、学法迁移实录

（1）动态关联：移一移

师（出示图4）：请移动点A和点B，观察图形的变化情况。

生：点B往左移，图形变成平行四边形，继续往左移，图形变成梯形；点A往右移，图形变成平行四边形，继续往右移，与点D重合时，图形变成三角形。

（2）学法迁移：延展结构

师：整体回顾一下，今天我们是怎么认识平行四边形和梯形的？

师：利用平行和垂直的知识，找平行线认四边形，造平行线做四边形，研究运动中的四边形。接下来我们还将学习什么图形？同学们可以利用今天的学习方法和材料，去学习更多与图形有关的知识。

钉子板上点的移动会引起四边形边和角的变化，这一现象使得学生能够在动态变化中理解图形本质，整体构建图形之间的关系，完善图形认识的网络。回顾总结时，笔者播放微课视频，引导学生不断思考现在学习的图形和以前学习的图形之间的联系，打破单元学习的界限，帮助学生构建更加系统的立体图形学习知识体系。

“认识平行四边形和梯形”不是一次简单的图形学习，教师应注重让学生在活动中完成思维进阶，注重知识之间的内在结构和关联，注重综合能力和核心素养的培养。因此，在平时的教学中，教师一定要细细研读《义务教育数学课程标准（2022年版）》、研究教材、研究学生，课前根据学生的需求精心设计，课中站在学生立场精彩调度，不断用适切的材料、丰富的活动、合适的支架帮助学生理解知识本质、引导学生主动关联，从而促进学生思维进阶及关键能力的发展。

［ 参 考 文 献 ］

[1] 中华人民共和国教育部.义务教育数学课程标准（2022年版）[S].北京：北京师范大学出版社，2022.

[2] 孙晓天，张丹.义务教育课程标准（2022年版）课例式解读  小学数学[M].北京：教育科学出版社，2022.

[3] 史宁中.推进基于学科核心素养的教学改革[J].中小学管理，2016（2）：19-21.

[4] 袁晓萍.整体关联 自然生长： “小数的初步认识”单元整体设计路径与实施[J].小学数学教师，2022（12）：42-46.

[5] 鄭虹.基于学生立场的学校课堂教学改进策略[J].课程教学研究，2022（6）：103-106.

（责编 吴美玲）