数还是一个“点”吗?
朱昭伟 林志辉


[摘 要]数源于数,准确数的教学使学生建立“数对应数直线上一个点”的认知,而近似数的教学则打破了“数对应数直线上一个点”的认知,使学生认识到近似数表示一个区间内的所有数,是一次“由点到线”的数的概念的认知突破。文章结合“小数的近似数”教学实践,通过缘起、实录、反思三部分,阐述如何带领学生在多元表征互译中实现“由点到线”的数的概念的认知突破,进而全面理解近似数的意义,发展数感。
[关键词]小数;近似数;数直线
[中图分类号] G623.5[文献标识码] A[文章编号] 1007-9068(2023)32-0066-03
一、缘起
在学习近似数之前,学生对数的认识都对应着一个具体的物象,即数在数直线上对应一个具体的点。近似数表示一个区间范围内的所有数,在数直线上它对应的不是一个点,而是一条线段。在“小数的近似数”之前,教材安排了近似数的初步认识、整数近似数等内容(首次提出用“四舍五入”法求近似數)。教材在“小数的近似数”中创设身高情境,通过与原有认知的连接,以对话的方式介绍了求小数近似数方法的探索过程。
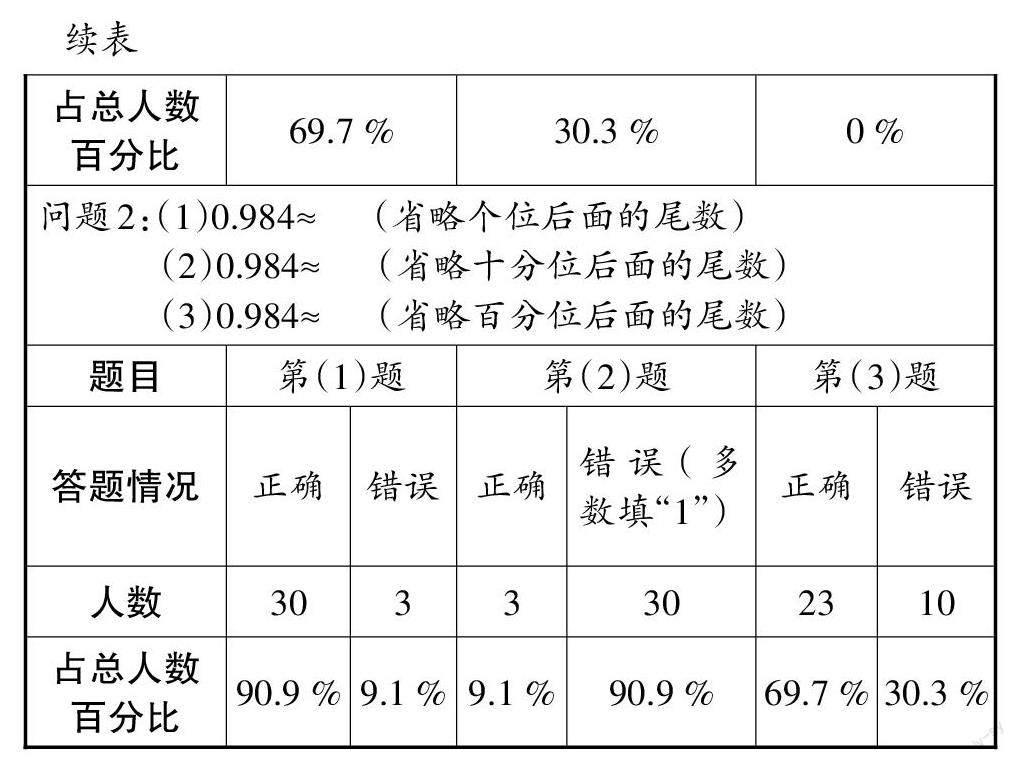
另外,笔者通过前测(见表1)发现:近似数这一概念对四年级的学生来说并不陌生,学生已有了用“四舍五入”法求整数近似数的经验,对近似数的意义有了一定的感悟。学生对求小数近似数的基本方法已不教而会,但对近似数1和1.0哪一个更精确却无法理解。由此可见,学生在这里出现了一个思维上的断层,也就是对近似数的意义缺乏深层次的理解。
那么,本节课如何带领学生突破认知障碍,全面理解近似数的意义呢?笔者尝试在多元表征互译中实现“由点到线”的数的概念的认知突破,将教学目标确定为:(1)理解小数近似数的意义,会用“四舍五入”法求一个小数的近似数;(2)经历求小数近似数的探索过程,通过类比、推理、想象,发展学生的数感;(3)感受数学知识之间的联系,收获成功的体验,提高学习兴趣。
二、实录
1.情境激活,迁移方法
(1)情境引入
师:猜一猜,老师的身高大约是 。若给你几个选项,你选哪一个?
(课件出示选项:A.1米 B.2米 C.1.8米 D.1.7米)
生1:老师的身高大约是1.7米,也可能是1.8米。
生2:老师的身高大约是2米。
(课件出示条件:老师的实际身高是1.745米)
师:现在你肯定不会选哪个选项?
生3:我肯定不选“1米”,因为1米太矮了。
生4:我觉得2米、1.8米、1.7米都有可能。
(2)聚焦“2米”
师:为什么2米也可以?
生4:实际身高是1.745米,省略个位后面的尾数时要看十分位,“五入”后就是2米。
(板书:保留整数 1.745≈2)
(3)推广方法
师:为什么1.7米、1.8米也可以?
生5:我觉得1.8米不可以,1.745保留一位小数时要看百分位,“四舍”后就是1.7,因此我认为可以是1.7米。
(板书:保留一位小数1.745≈1.7)
师:为什么1.745既可以约等于2,也可以约等于1.7?
生6:因为两者保留的位数不一样,如果保留整数,就看十分位,约等于2;如果保留一位小数,就看百分位,约等于1.7。
师:如果保留两位小数、三位小数,更多数位呢?
生7:无论保留到哪一位,都要看它的下一位。
(4)小结
师:求小数的近似数和求整数的近似数一样,即省略某一数位后面的尾数,要看那个数位的后一位。
【设计意图】此环节紧抓学生的认知冲突点,围绕新旧知识的连接点,厘清思维的模糊点。通过创设教师身高情境,以选择题为牵引,在“猜一猜”“正向选”“反向选”等活动中充分激活学生已有的知识经验,进而聚焦“2米”的冲突,使学生顺利将求整数的近似数的方法迁移到求一位小数的近似数活动中,再进行推广、延伸,使学生认识求小数近似数的方法,同时顺利将求小数、整数的近似数的方法相融合,实现正向迁移、方法同化。
2.以数助形,理解意义
(1)理解“近似数2”
①问题驱动
师:保留整数,约等于2的小数有哪些?请在数直线上表示出来。
②分层反馈
师(展示如图1所示的作品):猜猜看,1.5是怎么想到的?2.4又是怎么想到的?
生1:保留整数,要看十分位,2的左边是“五入”,最小是1.5;2的右边是“四舍”,最大是2.4。
师(展示如图2所示的作品):还可以是哪些小数?
生2:我觉得三位小数也可以,四位小数也可以,只要是在1.5和2.4999之间的小数都可以。
师:约等于2的小数在数直线上怎么表示?
生3:约等于2的小数要看十分位,最小是1.5,最大是2.49999…,也就是最大不超过2.5的小数。
师:最大不超过2.5我们可以用空心圈的方式来表示(适时教学不超过2.5在数直线上的表示方法)。
(2)对比“近似数2”和“准确数2”
师:近似数2和以前学过的准确数2有什么不一样?
生4:准确数2是一个点,近似数2是从1.5到2.5(不包括2.5)范围中的所有小数(如图3)。
【设计意图】本环节作为本课的课眼,以关键问题“保留整数,约等于2的小数有哪些?”为驱动,引题激趣后充分放手,让学生自主思考、实践和组内交流、全班反馈交流。多形式的思考、操作、观察、交流等,使学生的学习在时间和空间上有了充分的保障。另外,通过多层次的作品反馈、对比交流、数形结合,让学生经历“点—连续区间”这样一个小数近似数意义理解的过程。继而通过“近似数2”与“准确数2”的对比研究,数形结合,再次深化对近似数“从点到线”的认识。
3.数形结合,破难延伸
(1)突破“末尾0”难点
师:近似数是2.0,末尾的0能去掉吗?
生1:我认为能去掉,根据小数的性质,小数末尾的0能省略。
生2:我认为不能去掉,去掉后就成了近似数2了,近似数2.0和近似数2的范围不一样。
师(出示图4):现在你觉得2.0末尾的0能去掉吗?
(学生通过对比后认为不能去掉2.0末尾的0)
(2)想象延伸
师:想象一下,近似数2.000在数直线上是怎样表示的?近似数2.0000…呢?
【设计意图】“用小数表示近似数时,小数末尾的0不能去掉”这一知识始终是学生的认知难点。在本环节中,教师通过数形结合的方式,将近似数2、2.0、2.00进行多层次直观对比,帮助学生顺利破难。另外,在延伸环节让学生想象近似数2.0000…如何表示,向学生渗透了极限思想。
三、反思
近似数表示一个区间范围内的所有数,在数直线上是一段线。虽然课后学生及时做了大量练习,却依然对“用小数表示近似数时,小数末尾的0不能去掉”存疑。那么,这节课是要学生掌握方法还是理解意义?笔者认为这节课的教学关键是让学生深度理解小数近似数的意义。理通则法明,意义理解了,学生对求小数近似数的方法自然就清楚了,数感也随之得到相应发展。
1.顺势迁移,正向丰富
学生已经会了的不教,学生能自己学会的不教,教学要落在学生困惑迷思处,落在学生思维发展处。学生在之前的学习及生活中对近似数有着丰富的感性认识,前测也发现多数学生对于求小数的近似数的方法已有一定了解,且对近似数的意义已有所感悟。基于这样的学情,教师在课始创设身高的情境,通过“猜身高”“正向选”“反向选”等活动激活学生已有的知识经验,顺势迁移,将求小数的近似数的方法很好地“嫁接”在求整数的近似数的方法上。同时,采用问题冲突的方式进一步明确方法,并进行推广联结,使求小数的近似數与求整数的近似数方法相融合,顺利实现知识的同化,从而在正向上对近似数的意义进行丰富。
2.以数助形,逐步丰富
形少数时难入微,数形结合是常用的教学策略。小学教学以形助数多见,而以数助形时常缺失。在本课中,从“1.745保留整数约等于2”引出“保留整数,约等于2的小数有哪些”,然后放手让学生探索,最大限度保障学生的自主权。通过多层次展示学生数形皆备的作品,在数直线上从“10个一位小数”到“100个两位小数”再到“最小1.5,最大不超过2.5范围内的所有数”,重点引导学生从“要思考哪一位?”“最小是多少?”“最大不超过多少?”等关键处进行思考,助力小数意义的理解。
3.以形助数,再次丰富
数缺形时少直观,以形助数能使教学更直观。本课在多次问题冲突对比中借助形的直观丰富学生对小数意义的理解。先是近似数2与准确数2的对比(一段线与一个点),清楚地让学生感知两者的区别。再是近似数1.7、1.8、2.0这些保留相同数位近似数的动态对比,使学生对小数近似数的意义有了更深的理解。还有近似数2、2.0、2.00这些不同数位近似数的直观对比,帮助学生顺利突破近似数“从点到线”的认知难点,再次深度理解“近似数是一条线”。
(责编 覃小慧)

