解决实际问题 落实数学建模素养
孙莹


摘 要:数学建模是数学学科一大核心素养。数学建模通常应用于解决实际问题。通过分析解决近年来河北省数学中考的一道应用题,指导学生解决实际问题的思路、步骤、方法。从审题、分析问题、串联问题、迁移问题、解决问题的过程,发展学生能力,落实数学建模素养。
关键词:实际问题;数学建模;核心素养
中图分类号:G633.6 文献标识码:A 文章编号:1009-010X(2020)17-0037-03
核心素养在本质上体现的是数学的基本思想。《普通高中数学课程标准(2017年版)》明确指出:数学建模是对现实问题进行数学抽象,用数学语言表达问题、用数学方法构建模型解决问题的素养,并把数学建模作为数学六大核心素养之一。《义务教育数学课程标准(2011版)》也指出:模型思想的建立是学生体会和理解数学与外部世界联系的基本途径。數学建模能力是基础教育中学生要学习和掌握的一大能力。在初中数学的学习过程中,数学建模主要应用于解决实际问题,对广大学生来讲,是学习的难点;对一线教师来讲,也是教学的重点。下面以一道河北省数学中考题为例,介绍在解决实际问题的过程中,如何落实建模素养。
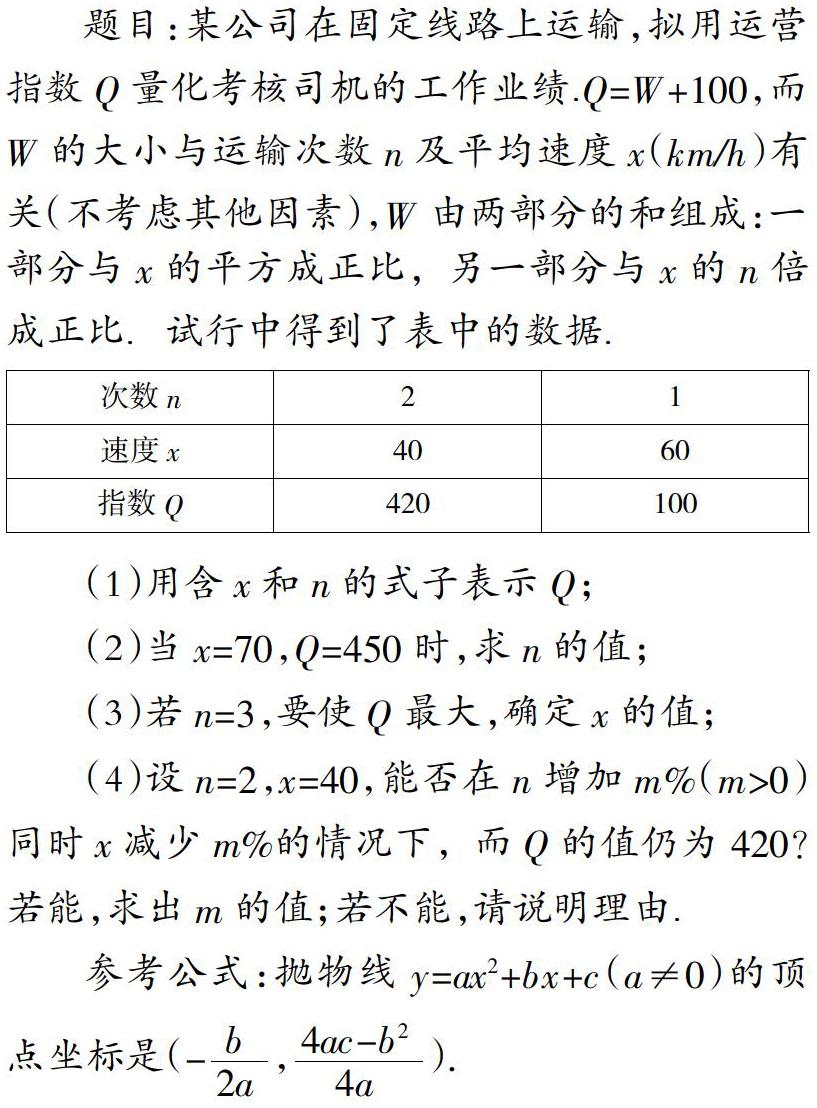
题目:某公司在固定线路上运输,拟用运营指数Q量化考核司机的工作业绩.Q=W+100,而W的大小与运输次数n及平均速度x(km/h)有关(不考虑其他因素),W由两部分的和组成:一部分与x的平方成正比,另一部分与x的n倍成正比.试行中得到了表中的数据.
一、审清题意是数学建模的前提
首先,要仔细阅读题干,了解题目背景,理解题意,明确问题。审题时需要梳理清楚题目中出现的“量”。在要解决的实际问题中,包含了哪些数量,这些数量之间又有怎样的关系?例如本题中,题干里有四个量:运营指数Q、过渡量W、平均速度x、运输次数n。其中,Q与W之间存在着Q=W+100这样的关系。而W与x、n之间的关系是:“W由两部分的和组成:一部分与x的平方成正比,另一部分与x的n倍成正比.”在理解这个条件时,就需要特别注意:构成W的这两部分的比例系数不一定相同,所以在建构W与x、n的关系时,需要区别这两个比例系数。
二、正确使用数学符号语言,是建模的必要条件
读懂题意后,学生要根据自己已有的知识经验,把题目中的关键的量与量之间的关系从自然语言转化成数学符号语言,抽象出数学关系式。例如:“W由两部分的和组成:一部分与x的平方成正比,另一部分与x的n倍成正比.”根据这个条件,我们可以先设出W与x、n的关系式,再得到Q与x、n的关系:
这样,在把文字语言转化成数学语言的同时,我们抽象出了Q与x、n的关系式:初步建立了函数模型。再利用我们熟悉的“待定系数法”确定函数关系式:
从实际问题中抽象出数学模型,需要教师在教学过程中教给学生正确使用数学符号语言,在审题的过程中,借助已有的数学经验和生活经验,合理引导,因势利导,建立有序的认知结构,从而使建立数学模型水到渠成。
三、在解决问题中,体会数学模型的作用
在初中数学的学习中,数学模型的作用主要体现在解决实际问题中。以本题为例,第1问获得的函数模型是解决后续的三个问题的关键。
函数的关系式中,一共有两个变量Q、x,n实际上是一个参数。此问中给出了两个变量Q、x的具体数值,很显然参数n可求。本问中,把函数模型转化成了方程模型,从函数关系式得到关于n的一元一次方程式,借助具体的数值与数量之间的关系,使函数模型过渡到了方程模型。
很显然,第3问与第2问相同,都是三个量中给出其中两个量的条件,求第三个量;但是与第2问也不同,这一问中给出的两个量,其中一个量是确定的n=3,另一个量不像第2问中直接明确给出了具体的值,而是:“要使Q最大”。所以本问难度上有所提升。但是,在解决问题的过程中发现,代入n=3的条件,得到了Q与n之间关系式,这个新获得的关系式,恰好是我们学习过的、熟悉的一个特殊的函数关系:二次函数关系式。因此,我们可以利用二次函数的性质通过求最值来解决。
在解决具体实际问题时,需要建立的数学模型往往不是单一的,本题以函数模型为主,同时,借助了函数、方程、不等式之间的内在联系解决问题。方程模型更有助于解决求未知量的问题,函数模型更善于刻画变化规律,解决最值问题,不等式模型往往用于解决求变元的取值范围问题。
四、模型亦可变,变中找不变
初中数学建模通常分为两种方式:通过运算法则建模或者通过已知条件中数量之间的关系建模。在解决实际问题时,后者更加常见,而且往往会出现二次建模或者多重建模。就像问题1中,先根据已知条件建立的函数模型,再建立W=k1x2+k2nx真正所需的模型:Q=k1x2+k2nx+100。即使是在同一个问题里,建立的数学模型也并不一定是一成不变的。就像本题的第4问:
面对同一个问题,解法、过程可能会有所不同,但是万变不离其宗,最后一定还是会归到同一个算理。另外,也需要特别注意,在用数学模型解决实际问题时,一定要对得到的结果进行检验,除了要符合数学关系式以外,还要符合实际的问题情境。
纵观全题,层层递进,环环相扣。学生在解决一个实际问题时,建立了一个数学模型。当学生在应用这个模型时,又遇到了一个新的问题,就需要我们在原有模型的基础上,重新构造数学模型。数学的学习是有序的,应用又是广泛的。具体问题具体分析,不是模型决定问题,而是以问题为导向,模型为解决是解决问题的工具。
《学记》中说:“学不躐等”“不陵节而施”。在数学建模中也一样适用。培养学生的数学素养,需要根据学生的已有学习经验和生活经验,循序渐进,自然水到渠成。
参考文献:
[1]中华人民共和国教育部制定.义务教育数学课程标准(2011版)[S].北京师范大学出版社,2012.
[2]余启宏,初中生数学建模素养发展的教学策略[J].中学数学,2020,(08):90~91.
[3]缴志清.初中数学教学关键问题指导[M].高等教育出版社,2016.
[4]张惠英.初小数学无缝衔接教材[M].河北教育出版社,2016.
[5]江建国,沈洪慧.让核心素养在经验生长中落地——以“基本不等式”(第1课时)为例[J].中国数学教育,2020,(08):39-41+51.
[6]中华人民共和国教育部制定.普通高中数学课程标准(2017年版)[S].人民教育出版社,2018.

