运动的精彩 想象的美妙
张浩
摘 要:在四年级下册开展“轴对称图形再认识”一课的目的是让学生在三年级轴对称图形的学习基础上感悟轴对称知识的本质——图形的运动.教学将“翻折”融入课堂,引导学生充分感知轴对称运动,使学生的认知层次上升到“理性认识”,知道轴对称图形的特征,让学生在观察和操作中,将对知识的思考与实物模型的演示有机结合,进而在头脑中形成表象、建立概念、以动促思、获得空间观念的发展,以此提升学生的数学素养.
关键词:轴对称图形;空间观念;数学素养
四年级下册的“轴对称图形再认识”教学,应在“轴对称图形”的几何实质上下功夫,即采用最合适的形式,使学生体会轴对称图形的几何实质——这也就是图形的运动方式.《义务教育数学课程标准(2022年版)》明确提出了数学教学的总体目标是“三会”,即“会用数学的眼光观察现实世界,会用数学的思维思考现实世界,会用数学的语言表达现实世界.”[1]为了实现课标要求,让核心素养在课堂落地,具体做法就是将“翻折”概念纳入课堂教学中,以通过这种可观测、可操纵、可表述的方式,引领学生全面认识轴对称运动,真正掌握点和图形之间变换的基本原理,并深入理解轴对称图形的基本特点,以此发展学生的空间观念,提升学生的数学素养.
1 精心观察图形,“对折”“翻折”变通途
由于在三年级上册学生已初步理解了轴对称图形的概念,能从直观上认识轴对称图形并加以区分,同时也掌握了用对折的方法对轴对称图形进行验证,这是学生对轴对称图形的已有经验.然而在上述学习过程中,大部分学生只感知了两边图形的形状和大小是一样的,对其图形的位置变化关注度不高,对轴对称图形的认识有偏差,空间观念欠佳.因此通过细致的观察,从“对折”引出“翻折”,顺应学生已有的旧知,让学生从多维角度去感知图形的运动,有利于为学生深入认识轴对称图形的特征打下基础.
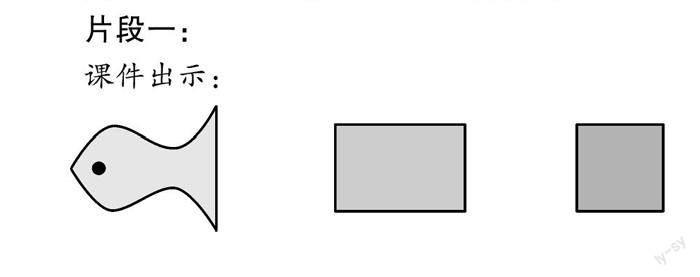
片段一:
课件出示:
師:“对折”可以判断一个图形是不是轴对称图形.
课件动态演示:把上述图形沿一条对称轴进行翻折.
师:现在再仔细观察,老师这里有个新的动作,你觉得叫什么?
生1:展开、翻过来、翻转……
师:你能演示一下这个动作吗?
让学生手势比划一下.
师:对的,你们所说的展开、翻过来,这个动作在数学上就叫“翻折”.
教师带着学生一起边做动作边说一说:把这半条小鱼图形沿着横着的对称轴向下翻折还原成了一条小鱼;这个小长方形沿着竖着的对称轴向右翻折还原成了大的长方形;这个直角三角形沿着斜着的对称轴向右上方翻折还原成了正方形.
小结:“翻折”可以把半个图形变成一个轴对称图形.
2 充分操作实物,“动”中所思长经验
四年级的学生空间想象能力不是很强,因此借助实物进行“翻折”操作,能在一定程度上强化学生的空间想象能力,同时多次“翻折”操作过程中也能突出本节课的重要内容之一“对称轴”,它是进行正确“翻折”的重要参考标准.轴对称图形的根本特点:对称点的连线与对称轴互相垂直、对称点到对称轴的距离相等,这些均和对称轴有关,故实物“翻折”操作让学生在“动”中感悟图形的运动变化,又在多次“翻折”后的不同轴对称图形对比中,培养了学生的空间观念.
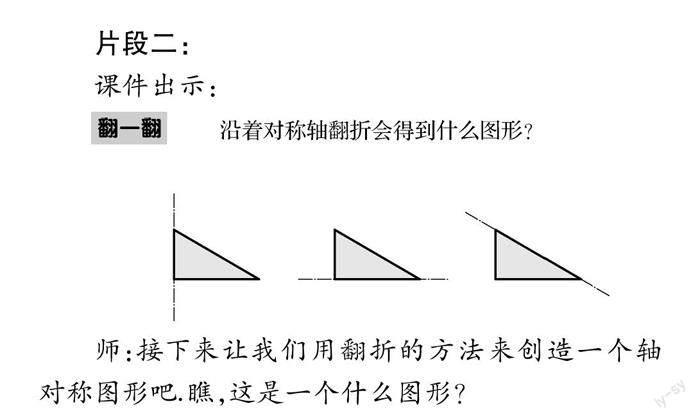
片段二:
课件出示:
师:接下来让我们用翻折的方法来创造一个轴对称图形吧.瞧,这是一个什么图形?
生2:三角形.
师:想象一下,这个三角形,如果以这条竖着的边所在的直线为对称轴进行翻折,会形成什么图形?谁愿意上黑板演示一下?
学生板演翻折后画出另一半,注意翻折的动作,不要与旋转混淆.
师:这个三角形除了可以沿竖着的边所在直线为对称轴进行翻折,还可以怎么翻折?
生3:还可以沿着横着的边或斜着的边所在直线为对称轴进行翻折.
师:请大家边想象,边动手翻一翻,再画一画,看看翻折后会得到什么图形?
学生操作翻折后画出另一半,再让两个学生进行板演操作.
师:为什么同一个三角形翻折后形成的轴对称图形不一样呢?
生4:翻折的方向不一样.
师:翻折方向不一样,也就是谁的位置不一样?
生5:就是对称轴位置不一样.
师:对称轴不一样,翻折出来的轴对称图形也不一样.看来对称轴很重要,是翻折的重要参考标准.
3 有效想象画图,本质特征蕴其中
对于认识轴对称图形的本质特征,本课反其道而行之,让学生去经历一个探究活动——翻折画图,补全轴对称图形的另一半,通过先想象,在脑中翻折,然后画出轴对称图形的另一半图形,让学生在操作和想象的加持下,再去发现性质,并解释道理.这样的练习,让学生对知识点的掌握更加彻底,紧扣“翻折”这样的图形运动方式,经历自主探究、思维碰撞的过程,让学生对技能的掌握更到位.最后通过点——线——面,图形的由来,勾连了“翻折”(新知)和“对折”(旧知)之间的联系,统一了轴对称图形的运动.
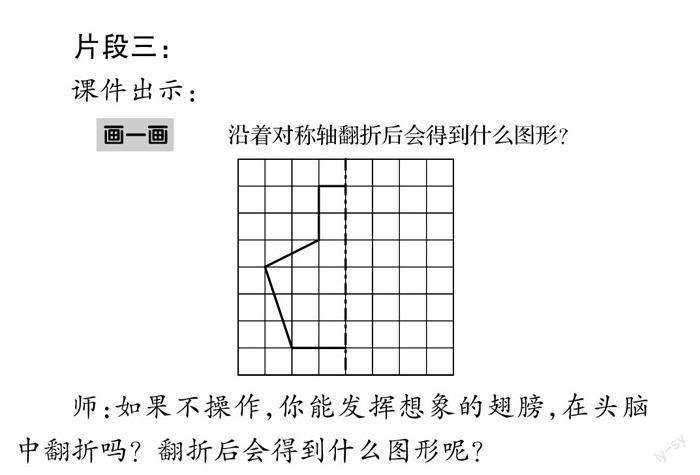
片段三:
课件出示:
师:如果不操作,你能发挥想象的翅膀,在头脑中翻折吗?翻折后会得到什么图形呢?
生:花瓶(水壶……).
师:是真的吗?你能不能把想象的花瓶画下来,为了精准,张老师给大家配了方格纸,请把你想象的图形画出来.
让学生操作画一画,再展示学生作业.
师:你们画出来的图形像花瓶吗?
生:像花瓶.
师:你们的想象力真不错,请你给大家介绍一下怎么画的呢?
生6:我直接画出和左边一半一样长的线.
师:很好,你关注了图形的线.(手指点)线画到这个点位置为什么拐弯往下画了,不画下去了呢?
生7:因为左边这点距离对称轴有1格,所以右边的点也要距离对称轴1格.
师:看来这个点的位置很重要.除了这个点,还有哪些点也很重要?
生找出点,师标出来图形中的对称点.
师:这些点的位置是由谁确定的呢?
生8:左右两个点距离对称轴的距离要一样.
再课件出示:左半个图形的顶点,并标上A、B、C、D.
师:为了方便交流,给这些顶点标上字母.你们找到的是这些点吗?(课件出示:A、B、C、D点的对称点)
生:是的.
课件动画演示:把花瓶图的左半边向右翻折.
师:把左半边图形翻折后,你们找到的4个点和A、B、C、D这4个点会怎么样?
生9:重合了.
师:其实这四个点就是A、B、C、D点翻折后的位置,数学上称它们为A、B、C、D点的对称点.A点的对称点用字母A′表示.都用到了A说明这两个点有联系,但又不一样,所以用了A′.那其他几个对称点可以用什么表示?
生:可以用B′、C′、D′表示.
师:接下去怎么办?
生10:连线.
师:现在将这几组对称点都连起来,请仔细观察,这些对称点的连线和对称轴之间有哪些联系?先和你的同学探讨问题,你会有哪些发现?
生11:对称点的连线与对称轴互相垂直;对称点到对称轴的距离相等.
师手指图形中左边的点(一个在边线格点处,另一个不在边线格点处).
师:这两个点有对称点吗?在哪里?
生板演指一指.
师:这幅图上像这样的对称点还有吗?
生12:有无数个.
小结:轴对称图形中只要左边有一个点,右边一定有一个点和它对称.
出示:把半个花瓶图翻折的动画.
师:如果把图形沿着这条对称轴对折,这些点会重合吗?点的连线会重合吗?线围成的图形会重合吗?所以对折后轴对称图形的两边是怎么样的?
生13:对折后轴对称图形的两边是完全重合的.
小结:通过探讨点和点之间的相互关系,发现轴对称图形的两个重要特点:对称点的连线与对称轴互相垂直;对称点到对称轴的距离相等.
4 多维判别错例,空间观念提素养
关于“一般的平行四边形是否是轴对称图形?”的判别一直是个难点,就算学生在三年级初步判断轴对称图形的练习中能用对折的方法加以验证,但过段时间再来判断时依然有学生会觉得一般的平行四边形是轴对称图形,这是因为学生更多地还是关注图形两部分是否相等,而非图形两部分是否重合,所以应该在图形的运动上下功夫,让学生在脑中进行想象翻折,勾勒出形,再通过图形上的点和点的位置关系深入分析一般的平行四边形的特点,最后勾连图形运动方式,对比分析小学阶段学习的刚体运动——平移、旋转、轴对称之间的联系和区别.能让学生在脑海中将感知到的信息与心理图式发生相互作用,得到图形感知能力和空间想象能力的有效锤炼和提升.
片段四:
课件出示:
师:小明的说法你同意吗?你能不能做小老师帮他解释解释呢?
生14:不同意.把平行四边形沿着这条直线对折,两边没有完全重合.
生15:不同意.沿着这条直线翻折,形成的图形不是平行四边形.
生16:这个图形的一半平移才是平行四边形,如果翻折的话就不是平行四边形了.
出示:平行四边形的一半.
师:如果把这一半图形沿着这条对称轴翻折,会是什么图形?
让学生用手势翻折回答.
师:跟着老师一起翻折看看,会是什么图形呢(课件出示翻折动画)?和你想的一样吗?
生17:翻折后像一个箭头.
师:我们发现翻折后的图形不是平行四边形,说明小明的想法是错误的.
再課件出示:
师:思考图形中这组对应点的连线和折痕所在直线的关系,你有什么发现?
生18:平行四边形的对应点连线和折痕所在直线不是互相垂直,说明这条直线不是对称轴,这个平行四边形不是轴对称图形.
师:从轴对称图形的特征也能说明小明的说法是错误的.
出示:平行四边形的一半进行平移运动,组成了一个平行四边形.
师:看这半个图形进行了什么运动,组成了一个平行四边形?
生19:这半个图形进行了平移,组成了一个平行四边形.
师:图形运动的方式不一样,运动后图形的位置不一样,所以得到的图形也不一样.我们从多方面判断这个平行四边形不是轴对称图形,使我们对平行四边形又有了更深入的认识.
5 重视运动探究,透过现象看根本
运动是世间万物的基本特征,是物质存在的基本形式.平面图形的运动,对学生认识丰富多彩的现实世界、建立基本的空间观念,以及提高对图形美的体验和鉴赏能力都具有非常关键的意义.学生在学习平移、旋转、轴对称这些内容时主要通过操作活动积累基本活动经验、获得直观感受.由于图形的运动是一种最主要的数学思维方式,所以不但要使学生了解运动的结果,还必须让学生想象运动的过程,进而理解平移、旋转和轴对称运动的本质意义,即平移、旋转、轴对称运动有一个共同的特征,就是运动之后保持任意两点之间的相应距离不变,这也就确保了运动之后物体的形状、大小不变.通过具体情境“这条小鱼图的面积是多大呢?”,让学生进一步认识图形的这种刚体运动,渗透同学间相互合作的意识,体会运用数学知识解决实际问题的实用性.让学生认识图形运动的一个主要目的是引导学生运用数学的眼光观察现实世界,让学生能够逐渐懂得在生活中观察和欣赏图形的运动现象,进一步感受数学对人类发展的意义,感受数学的文化教育意义.通过观察从轴对称运动引出中心对称运动,有利于学生在以后体会到“立体图形也基本都是由平面图形运动引起的”,从而开启了学生的视野,进一步发挥了学生的个性和创新能力,领悟了图形世界的奇妙,调动了学生的数学学习积极性,让学生体会到了数学的实际应用价值.利用图形的运动探索认识和证明图形的某些特性,从而促进了学生对探索图形特性的浓厚兴趣,让学生体会到探索图形特性可以有不同的途径.
片段五:
课件出示:
师:这条小鱼的面积是多大呢?
让学生讨论、合作:同桌对折后的两个半条小鱼图可拼成一个长方形 .
课件动态演示:水平方向把小鱼图平分,把下面半条小鱼图旋转,再以水平方向为对称轴,将下半部分翻折上去,最后平移.
师:现在你们会求这条鱼的面积了吗?
生20:把鱼转化成了长方形,长方形的面积就是鱼的面积.
师:通过平移、旋转、轴对称这些图形的运动巧妙地把不熟悉的图形转化成我们熟悉的图形,小鱼图的面积和转化后长方形的面积是一样大的.
出示:
师:其实轴对称图形只是所有对称图形中的一种,那么除了轴对称图形还有哪些呢?你看,平行四边形(出示),它是对称图形吗?
生21:不是轴对称图形.
生22:是中心对称图形.
师:对,我们绕着中心点旋转180°,它是不是重合了?(课件动态演示)
这就是中心对称图形.
师:长方形是轴对称图形,还是中心对称图形?仔细看.(课件动态演示)
小结:看来对称图形还有很多,轴对称图形只是其中的一种.
师:如果把这个长方形沿着长(或宽)旋转一周,又会是怎样的图形呢?你又有什么新的发现吗?
生:……
一种概念的产生,是指学生将现有经验活化后更新的产物.就轴对称图形的概念来说,采用“翻折”这种经验展开教学活动,不但有助于学生了解图形运动的实质,同时也促进了学生空间想象能力的发展,更主要的是可以改变学生的思考方法,即用运动的眼光认识空间图形、探究几何图形问题.
参考文献:
[1] 中华人民共和国教育部.义务教育数学课程标准:2022年版[S].北京:北京师范大学出版社,2022.

