深研概念教学,厘清“来龙”和“去脉”

潘永斌

摘 要：本文以“函数的单调性”的教学设计为例，分析了在教学过程中，如何厘清数学概念的“来龙”与“去脉”，突破数学抽象的难点，以期为教师在后续教学中更好地开展概念教学和大单元教学提供思路与启发.

关键词：函数的单调性;数学抽象;教学设计；大单元数学

“函数的单调性”作为高中阶段学生接触并研究的第一个函数性质，通过函数单调递增（减）、增（减）区间以及增（减）函数概念的生成，逐步完善了“函数的单调性”的知识体系.同时，在江苏凤凰教育出版社出版的《普通高中教科书·数学》必修一中，给出了利用数学抽象研究函数单调性的步骤与方法，为学生后续研究函数的奇偶性等性质以及具体的基本初等函数的性质提供了依据，在函数性质的研究方法层面上逐步形成系统.

笔者将以“函数的单调性”的教学设计为例，谈一谈对概念教学、大单元教学的粗浅理解，以及如何在获得数学概念的数学抽象的过程中，厘清概念教学中的“来龙”与“去脉”，以便在后续教学中更好地开展概念教学和大单元教学.

1 数学抽象的作用和意义

《普通高中数学课程标准（2017年版2020年修订）》（以下简称《标准（2017版）》）提出数学抽象、逻辑推理、数学建模、直观想象、数学运算与数据分析六大数学学科核心素养，其中数学抽象位居首位.数学抽象作为数学产生和发展的思维基础，反映了数学的本质特征，是数学学科核心素养的重要组成部分.

数学抽象的作用和意义主要体现在如下几个方面：（1） 获得数学概念和规则是数学抽象的一个重要表现；（2） 提出数学命题和模型是数学抽象的一个重要过程；（3） 数学方法与思想是数学抽象的一个重要产物；（4） 认识数学结构与体系是数学抽象的一个更高水平.

2 获得数学概念的数学抽象过程

根据抽象程度的不同，史宁中教授将数学抽象过程细分为三个阶段：一是简约阶段，把握事物本质，把复杂问题简单化并条理清晰地表达；二是符号阶段，去掉事物的具体内容，利用符号和关系术语等表述已简约化的事物；三是普适阶段，通过假设和推理，建立法则或者模型，能在一般意义上描述具体事物的特征或规律.这三个阶段相互连接，后一个阶段建立在前一阶段的基础之上.

数学概念的获得包括概念形成和概念同化两种基本方式.数学概念的形成，通常会经历以下三个阶段：首先，从直观的背景、具体的材料中抽离出事物的本质特征；其次，对抽象概括的对象给予一般表示，并且用符号进行表述；最后，根据符号阶段得出的结论进行定义，形成概念系统进而应用.

函数单调性概念的建构过程充分体现了数学抽象的三个阶段：

第一阶段是抽离出事物的本质特征，建构函数单调性的具象意义，以图形语言表征——在什么范围内图象是逐渐上升的，在什么范围内图象是逐渐下降的.

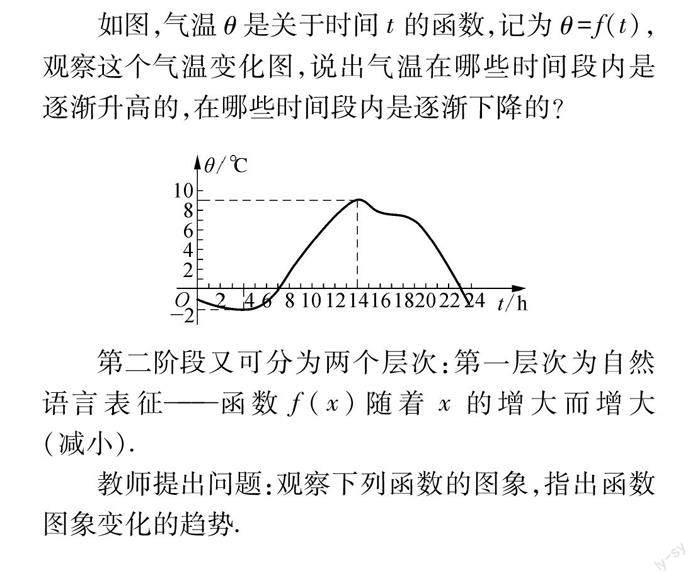
如图，气温θ是关于时间t的函数，记为θ=f（t），观察这个气温变化图，说出气温在哪些时间段内是逐渐升高的，在哪些时间段内是逐渐下降的？

第二阶段又可分为两个层次：第一层次为自然语言表征——函数f（x）随着x的增大而增大（减小）.

教师提出问题：观察下列函数的图象，指出函数图象变化的趋势.

学生提炼出自然语言表征：图象的这种“升”（“降”）的规律反映了随着自变量x的增大，函数值增大（减小）.

第二层次为符号语言表征——x1，x2∈I（其中ID，D为函数f（x）定义域），当x1＜x2时，都有f（x1）＜（＞）f（x2）.

第三阶段是单调递增（减）、增（减）区间、增（减）函数等概念的生成及应用.

3 函数单调性概念的数学抽象的难点

3.1 用符号语言表征函数的单调性的必要性

最直观的、最简单的得出函数单调性的方法当然是观察函数图象的上升或者下降的趋势，这也就是单调性的图形语言；要将图形语言表示成自然语言，就是要判断函数自变量增大时，函数值到底是增大还是减小，这是求函数极值和最值的关键；而用符号语言来表示自然语言，从而利用符号语言来判断函数的单调性，是学习函数单调性的根本目的之一.不难看出，表征函数单调性从图形语言到自然语言最后到符号语言的转化过程，是一个难度逐渐加大的过程，也是单调性这个概念逐步深化的过程.因此，从教学的角度而言，从图形语言到自然语言和符号语言的过渡是教学中的重点和难点.这一过渡，一般来说可以用“图形反映出的这种变化趋势用语言或数学符号该怎么描述”来完成，但是这样的处理方式，容易让学生产生“多此一举”的想法——既然用图形可以判断，何必还要用自然语言或符号语言来表示呢？概念建構过程中要让学生意识到用符号语言表征的必要性.

函数的单调性这一节的教学应当经历数学抽象得出概念并应用概念的过程，让学生看清楚数学知识的发生和发展过程.对于已知图象或者可以画出图象的函数，可以借助函数的图象直接予以判断；可倘若已知函数解析式，却出于某种原因暂时难以画出甚至画不出图象，此时就需要借助新的代数方法对函数的单调性作出判断，这就是用符号语言表征函数单调性的“来龙”之一——必要性.学习函数的单调性后，借助代数方法对函数的单调性作出判断，然后大致画出函数图象的示意图，进而直观感受函数的特征，这就是用符号语言表征函数单调性的“去脉”之一.

3.2 函数单调性概念的数学抽象的难点及突破

通过对具体图象的观察得到变化趋势的直观感知，以图形语言和自然语言进行表征，这个过程对思维要求较低.单调性概念的数学抽象主要难在用符号语言来形式化表征单调性时，如何最大限度尊重并引导学生建构“自己的表达”.笔者提供如下两种设计思路，供同仁参考（以“函数f（x）随着x的增大而增大”为例）.

设计一：利用极限无限逼近的办法来刻画x1、x2间的关系，实现从有限到无限的突破，再利用有限来表达无限.

而利用极限思想来分析问题、解决问题的能力在学习渐近线（函数图象、双曲线）、瞬时变化率、导数的概念时显然是不可或缺的.

设计二：条分缕析，用符号语言来分步逐句翻译、表征“函数f（x）随着x的增大而增大”.

这其中又有两大思维难点：其一是“x增大”和“f（x）增大”中的“增大”如何用符号语言进行表示；其二是对于“函数f（x）随着x的增大而增大”，如何用符号语言表示“随着”.

3.2.1 如何用符号语言表示“增大”？

“增大”意味着需要比较两个量，“增大”表现的是持续的变化状态，显然不可以用具体数值来刻画“持续”，由于字母具有一般性，可用字母表示数.这样逐步引出用不等式和字母来进行表达，即“x1＜x2”和“f（x1）＜f（x2）”.

3.2.2 如何将“随”符号化？

当x1＜x2时，有f（x1）＜f（x2）.

用符号语言来分步逐句翻译、表征自然语言，是每位学生学好数学的基本功，是后续对称性、周期性等内容学习的基础.

能否引导学生从有限→无限→所有→任意或者从静态→动态→所有→任意不断实现跨越，能否确保每一次过渡做到水到渠成不生硬，除了要看教师是否具备良好的教学基本功和能否较为合理地设问外，有没有“来龙”同样至关重要.

事实上，江苏凤凰教育出版社出版的《普通高中教科书·数学》必修一第二章《简单逻辑用语》第三节全称量词命题和存在量词命题中是这样定义的：“所有”“任意”“每一个”等表示全体的词在逻辑学中称为全称量词（Universal Quantifier），通常用符号“x”表示“任意x”.全称量词命题：x∈M，p（x）.

任意x1，x2的“来龙”正在于此，这也正是突破单调性概念的数学抽象的最难点的“来龙”.

4 深研概念教学，厘清“来龙”与“去脉”

在高观点下对知识进行系统梳理以及完整描述某个数学领域的知识体系，可以让学生理解通过数学抽象获得知识的重要性及必要性，进而展现数学抽象的独特魅力.

能熟练地进行图形语言、自然语言和符号语言之间的相互转化是数学学习和研究的基本功.多种语言形式的相互表征，也为后续学习对称性（奇偶性）、周期性、线面垂直的判定、瞬时变化率、导数等提供了知识和方法上的准备.

函数单调性概念的数学抽象过程中的难点和关键之处既是全称量词与存在量词命题的“去脉”，又是对称性（奇偶性）、周期性、线面垂直的判定、瞬时变化率、导数等學习的“来龙”.

整个函数的单调性概念的数学抽象过程展现出数学知识的“来龙”“去脉”以及知识结构的延续与升华，其中所包含的由有限到无限再化无限为有限的思想也充分展现了数学的哲学内涵.

抽象的步骤、方法可以运用到新的问题研究中去，抽象出来的知识可以运用到实际生活和实践中.同时，在这个过程中，数学抽象的魅力也体现在可以化无限为有限，通过有限的对象来替代无限的对象，进而简化研究问题.极限思想的启蒙，为后续导数概念的生成奠定了基础.而这些，都是抽象的“去脉”.

了解数学理论体系及完善过程，理顺不同知识模块、研究领域之间的联系与统一性，并对数学结构与体系进行抽象有助于我们看清知识的“来龙”与“去脉”.在整个高中数学结构与体系中，这样的“来龙”与“去脉”还有很多.教师只有深入挖掘、深刻领会，才能在大单元教学中，厘清概念教学中的“来龙”与“去脉”，进而帮助学生厘清高中数学学习中概念知识生成、思想方法习得的“来龙”与“去脉”.

参考文献：

［1］ 中华人民共和国教育部.普通高中数学课程标准（2017年版）［S］.北京：人民教育出版社，2018.

［2］ 史宁中.数学思想概论（第1辑）：数量与数量关系的抽象［M］.长春：东北师范大学出版社，2008.

［3］ 李昌官.数学抽象及其教学［J］.数学教育学报，2017（4）：61-64.

［4］ 张宗余，冯斌.数学抽象，数学概念教学抹不开的情愫［J］.数学通报，2017（2）：33-35+63.

［5］ 章建跃.高中数学教材落实核心素养的几点思考［J］.课程·教材·教法，2016（7）：44-49.