小学生空间观念培养微探

饶新彪

【摘要】小学生的空间观念与大脑中的表象有着密切的关系，是他们认识客观世界的一种重要形式，并且在需要的时候这种表象能被重新加以具体化.农村小学生发展空间观念的基本途径有：对学习、生活经验的回忆，实物观察、动手操作、想象与表达活动等.

【关键词】回忆；猜想；想象；表象；空间观念

《义务教育数学课程标准（2011年版）》指出：“空间观念主要是指根据物体特征抽象出几何图形，根据几何图形想象出所描述的实际物体；想象出物体的方位和相互之间的位置关系；描述图形的运动和变化；依据语言的描述画出图形等.”大量的实验研究表明，小学生空间观念的形成具有明显的直观性、描述性、渐进性以及偏重于某些明显要素、单个要素等特点.同时，农村小学生发展空间观念的基本途径有：对学习、生活经验的回忆，实物观察、动手操作、想象与表达活动等.

一、回忆——激活经验，唤醒表象

对儿童来说，空间观念是在日常生活与学习过程中通过积累起来的经验而发展起来的，经验的积累是他们发展空间观念的基础.他们在生活中已积累了许多有关物体、几何形体的经验认识与感受，通过有效地激发、回想，唤醒头脑中已有的经验表象，如，长方形、长方体、圆形、圆柱体等形状的表象，并以此作为新知识学习的生长点.但他们的经验表象是粗糙的、肤浅的、非数学化的，通过教学进一步提升学生的经验认识，运用数学化的方法对他们头脑中的经验表象进行加工、处理，使其更加清晰、完整，逐步完善、建构有关几何形体的正确的数学表象.这样不仅促进了知识的正迁移作用，而且有利于学生空间观念的形成与发展.

二、猜想——发散思维，再创表象

如，《长方形的面积计算》新授课，在巩固练习时，教师提出了这样一个问题：一个长方形面积是24 cm2，请你猜想一下，它可能是怎样形状的长方形？

生1：这个长方形的长可能是6 cm，宽可能是4 cm.

生2：也可能长是8 cm，宽是3 cm.

生3：可能长是12 cm，宽是2 cm.

生4：也可能它的长是24 cm，宽是1 cm，是扁长的.

……

学生刚刚学习探究出了长方形面积的计算方法，头脑中已初步形成了长方形面积与长和宽关系的表象图式，即长边摆的面积单位数乘以宽边摆的面积单位数的积就是长方形的面积单位数.当教师只告诉学生一个条件：长方形面积是24 cm2，让学生猜想这个长方形的形状.学生头脑中便能迅速浮现长方形的表象，然后再根据给定的条件“面积是24 cm2”，进一步对于头脑中的长方形表象进行加工、处理，使其长边与宽边的乘积是24个面积单位.当学生每说出一个长方形的长度与宽度时，头脑中也会伴随相应的表象活动，这样，数形结合，不仅实现了新知识的内化与运用，而且有利于学生空间观念的培养与发展.

三、想象——虚拟表象，发展思维

想象是培养儿童空间观念的一个重要途径.根据内容的新颖程度，想象可以分为再现想象和创造想象，在小学阶段，最基本、最常用的就是再现想象，即根据有关描述在学生头脑中形成相应形象，它是培养学生空间观念的一条重要途径，也是培养学生想象能力的基础.

如：在教学认识圆锥体的高时，由于对圆锥的高学生较难掌握，这时就要引导学生运用电脑动画演示，然后再通过学生动手操作学具，让学生在“观察→操作→再观察→想象”中抽象出圆锥的高这一概念.

又如：《长方体的体积》教学，在学生已经知道长方体的体积就是长方体所含有的体积单位的个数时，教师启发学生用1立方厘米的体积单位来研究长方体的体积计算方法：

师：（出示12个体积单位都是1立方厘米的小正方体）.试一试摆成长方体，有几种不同的摆法，每一种长方体的长、宽、高分别是多少？怎样计算长方体所含有的体积单位数？

学生展示摆出的图案：

生1：摆出三种长方体长、宽、高分别是12厘米、1厘米、1厘米.

生2：摆出三种长方体长、宽、高分别是4厘米、3厘米、1厘米.

生3：摆出三种长方体长、宽、高分别是3厘米、2厘米、2厘米.

师：刚才你们动手操作的几种摆法，长方体的体积都是多少？

生：都是12立方厘米.

师：如果仍给同学们12个体积单位都是1立方厘米的小正方体，你能摆出体积比12立方厘米大的长方体吗？

学生先是好奇，感到疑惑，然后尝试动手摆一摆后回答.

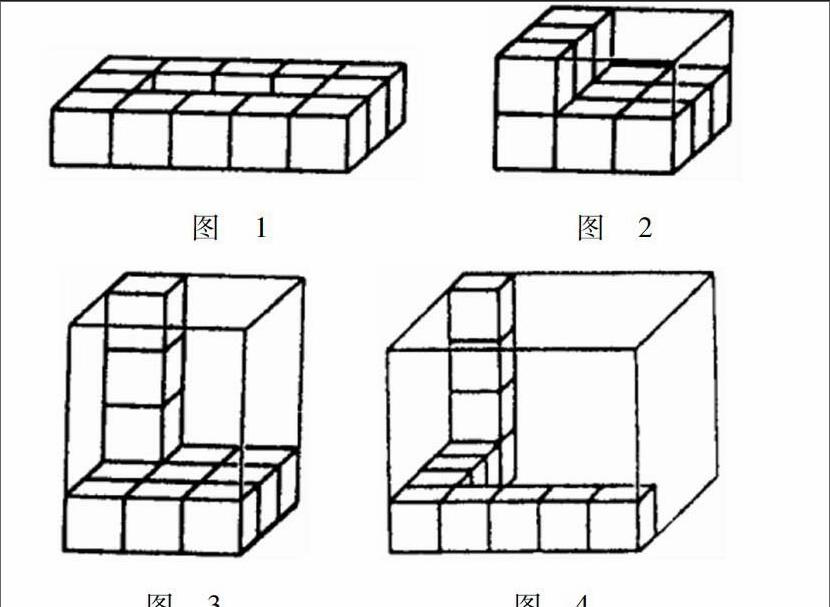
生1：我用12个体积单位都是1立方厘米的小正方体摆成长一行有5个1立方厘米，中间头尾各摆一个空三个，我想象成也是5个1立方厘米.宽有这样的3行，摆了一层，体积是15立方厘米.（如图1）

师：你这个想象好.还有不同的摆法吗？

生2：长一行摆3个1立方厘米，宽有这样的3行，一层就是9立方厘米，再把3个1立方厘米的小正方体摆在上面，凭着想象，表示摆了两层，体积是18立方厘米.（如图2）

师：这名同学是借助想象摆了一个虚拟的长方体.那你再说一说想象的长、宽、高分别是多少？（长3厘米、宽3厘米、高2厘米）

生3：老师，我把上面第二层的3个小正方体竖起来，就有这样4层的虚拟长方体了，体积就更大了.一层是9立方厘米，4层就是36立方厘米.（如图3）

师：你很牛.那你再说一说想象的长、宽、高分别是多少？（长3厘米、宽3厘米、高4厘米）

师：谁还能摆一个体积比他们更大的虚拟的长方体吗？

生4：可以用12个小正方体分别表示出长、宽、高，长5厘米、宽5厘米、高4厘米，这样组成的虚拟长方体体积更大.（如图4）

……

通过摆一摆、说一说，教师借电脑多媒体演示，学生欢欣鼓舞，感受到动手探究成功的喜悦.加深了对长方体的体积的认识以及从长方体的一个顶点引出的三条棱（分别是长方体的长、宽、高）之间的关系有了更加直观的认识.

教师第一次提出用体积单位都是1立方厘米的小正方体摆一个长方体，学生顺利地完成了任务，并根据自己摆的形状计算出长方体的体积单位数.这是学生第一次初步感知长方体的体积与长、宽、高之间的关系，这只是初步的感知活动.

当教师第二次布置任务，要求摆一个比体积是12立方厘米更大的长方体，制造了一个矛盾冲突，使问题与操作活动具有挑战性和创造性，大大地激发了学生的探究兴趣和欲望，学生的思维处于积极活跃的状态，他们凭借体积单位教具实物模型，通过摆一摆、拉一拉，充分地发挥想象作用，经过尝试，学生在头脑中构建一个虚拟的长方体模型，以及形成长、宽、高的表象并计算其体积.这一阶段学生的想象活动经历了三个层次阶段：对长方体内部的虚拟想象→对长方体某一部分的虚拟想象→框架构造的整体虚拟想象.这种“框架构造”的思想正揭示了长方体体积与其长、宽、高关系的实质，长方体体积的计算方法在学生的脑海中经过一次次的想象逐步孕育成熟，瓜熟蒂落.这一想象活动，不仅实现了学生对长方体体积计算的深层建构与内化，对于农村小学生空间想象能力的培养具有极其重要的意义.

我们“空间与图形”知识的教学除了要关注再现想象能力的培养，还应关注提供创新想象甚至是幻想的空间.而创新想象最终都是以创新性的创作活动为表现形式的，因此，我们必须关注留给学生创作的空间.如学习了对称图形以后，可鼓励学生大胆想象，创作出优美的对称图形.学习了长方体的认识以后，可以以基本图形，想象并设计出各种事物，从而有效沟通数学与生活的联系.

【参考文献】

[1]中华人民共和国教育部.义务教育阶段国家数学课程标准（2011年版）[M].北京：北京师范大学出版社，2012.

[2]李萍.小学生空间观念培养的教学策略探析[J].西北成人教育学报，2013（1）.

[3]解莉，杨宏.“用数对确定位置”教学实录与评析[J].小学数学教育，2014（5）.

[4]王尚志，胡凤娟.理解把握数学课程中的核心概念（一）[J].小学数学教育，2012.