以核心素养为导向渗透数形结合思想的方法

庞宇棋

【摘要】圆锥曲线是高考数学的难点之一，而高考数学试题中，圆锥曲线的定点问题又常常作为压轴题，其对学生来说是一个不小的挑战.文章给出2022年高考数学乙卷理科圆锥曲线大题的六种解题方法，基于核心素养导向对该题的解题策略进行分析，说明数形结合思想在解决圆锥曲线压轴题中的有效性，并给出相应的教学建议，以供参考.

【关键词】核心素养；高考数学；圆锥曲线；数形结合；解法探究

引 言

根据《普通高中数学课程标准（2017年版2020年修订）》要求，高中数学课程要注重发展学生的数学学科核心素养.2022年高考数学以数学课程标准为依据，突出对数学学科核心素养的考查，强调数学思想方法的渗透与数学知识之间联系的体现，对学生的直观想象、逻辑推理和数学抽象等核心素养都提出了更高的要求，引导学生进一步把数学知识和方法内化为自身的知识结构，体现了“核心素养导向、数学能力为重”的命题原则.

圆锥曲线是高考数学中技巧性最强的一类题目，也是高考数学的难点之一，而数形结合思想是解决圆锥曲线问题的“关键武器”.在解题的过程中，学生可以借助图像使数学问题更加明确，进而找到问题的根源并解决问题.根据对近几年高考数学试卷的分析，应用数形结合思想解答的题目在高考数学中所占的比例越来越高，所以教师要在今后的教学中更加重视对学生数形结合思维的训练，引导学生熟练掌握圆锥曲线这类问题的解题方法和技巧，并注意在练习中总结解题规律，把“数”和“形”结合起来，提高发散性思维、创新性思维和触类旁通的能力.

一、题目呈现

直線过定点问题的常见解法为：①用参数表示出直线的方程，根据直线方程的特征确定定点的位置；②从特殊点入手，先确定定点，再证明该定点符合题目条件.求出直线方程是判断直线是否过定点的前提和关键.

1.常规联立法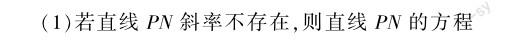

结 语

教师应当使学生了解圆锥曲线中极点极线的应用方法，弄清楚这类问题的实质，做到知其然并知其所以然.这样可以培养学生的数学核心素养和发散性思维，帮助学生完成数学知识体系的建构，从而能够触类旁通、举一反三.

【参考文献】

[1]陈熙春.2022年全国高考乙卷第20题的解法探究与拓展[J].理科考试研究，2022（21）：16-20.

[2]刘艳.圆锥曲线中一类定点问题的探究与思考[J].中学数学研究：华南师范大学版，2022（21）：33-35.

[3]王汉芹，刘玉华.把握数学知识本质 培养数学运算素养：以二轮复习课“圆锥曲线背景下直线过定点问题”为例[J].数学通讯，2022（16）：18-20，43.