复习课：从知识走向素养

杨清

【摘要】文章以“中心对称图形———平行四边形”设计为例，利用多媒体信息技术，以“旋转”为主线，从复习旋转入手，到旋转特殊角180°，再到旋转任意三角形、旋转特殊（直角和等腰）三角形开展探究.

【关键词】初中数学；复习课；旋转；中心对称；平行四边形；素养

【基金项目】本文系教育部人文社会科学研究项目“中小学生课堂学习机会评价模型的构建与应用研究”（项目编号：20YJC880134）研究成果.

“炒冷饭”式的初中数学复习课只注重知识回顾和习题练习，这样的复习课，学生只学会了知识而非素养养成.有效的复习课既能揭示知识间的实质联系，又能教会学生灵活运用知识，还能发散数学思维，培养学生的数学核心素养.基于这些思考，笔者结合教学实践进行了一些尝试.下面以“中心对称图形———平行四边形”的教学为例，浅谈章尾复习课应该如何设计和实施才能从知识走向素养.

一、研究教材，分析学情

“中心对称图形———平行四边形”是苏科版八年级下册第九章内容，涉及旋转、中心对称、平行四边形和特殊平行四边形（矩形、菱形、正方形）性质和判定，知识点较多，学生容易混淆且不会灵活运用.鉴于此前学生已学习了“图形的平移”“轴对称与轴对称图形”，初步积累了一定的图形运动变化的教学活动经验.本节课利用多媒体信息技术，以“旋转”为主线，从复习旋转入手，到旋转特殊角180°，再到旋转三角形、旋转特殊的三角形来开展学习探究.

二、环环相扣，层层推进

环节一：探究活动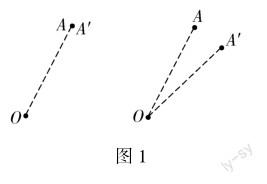

活动1 如图1，将点A绕着点O旋转，有哪些不变的量？

教师使用几何画板演示“点A绕着点O旋转的过程”，让学生回忆什么是旋转.有了动图的直观演示，学生更易回忆出旋转的三要素：旋转中心、旋转角度、旋转方向.教师提问：在这个过程中有哪些不变的量？唤醒学生大脑中对旋转的性质认识：OA=OA′，即对应点到旋转中心的距离相等.

活动2 如图2，将线段AB绕着点O旋转，有哪些等量关系？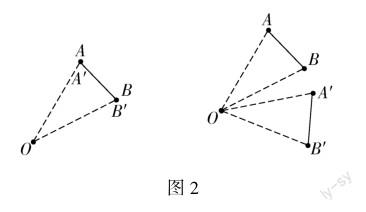

教师使用几何画板演示“线段AB绕着点O旋转的过程”，让学生说一说在旋转的过程中有哪些等量关系.通过观察动态旋转的过程，学生互相补充得到：OA=OA′，OB=OB′，AB=A′B′，∠AOA′=∠BOB′，即对应顶点与旋转中心连线所成的角相等，它们都是旋转角；△AOB≌△A′OB′，即旋转前后的两个图形全等.

教学说明：活动2是活动1的递进.活动1是通过旋转一个点帮助学生回顾“什么是旋转”“旋转的三要素”“旋转的性质”，活动2是通过旋转一条线段帮助学生进一步回顾旋转的性质.

活动3 如图3，将△AOB绕着点O旋转180°.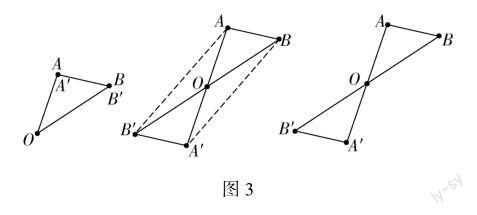

几何画板演示“△AOB绕着点O旋转180°”的过程.

师：将△AOB绕着点O旋转180°时，△AOB与△A′OB′有什么关系？

生1：两个三角形全等，AB∥A′B′.

生2：两个三角形成中心对称.

师：中心对称有哪些性质？

生：因为旋转，所以OA=OA′，OB=OB′，即对称点连线经过对称中心，且被对称中心平分.

师：如图3，几何画板连接AB′，A′B，构成的四边形AB′A′B是什么图形？你能说明理由吗？

生1：由旋转得OA=OA′，OB=OB′，对角线互相平分，四边形AB′A′B是平行四边形.

生2：AB=A′B′，AB∥A′B′，一組对边平行且相等，四边形AB′A′B是平行四边形.

生3：可以证明△AOB′≌△A′OB，AB′=A′B，AB=A′B′，两组对边相等，四边形AB′A′B是平行四边形.

生4：AB′∥A′B，AB∥A′B′，两组对边平行，四边形AB′A′B是平行四边形.

教师总结学生回答中的平行四边形的判定方法，并提出问题“你还记得平行四边形有哪些性质吗？”

教学说明：活动3是活动2的递进.活动3将△AOB绕着点O旋转特殊角180°，帮助学生回顾“什么是中心对称”“中心对称有哪些性质”，让学生经历研究数学问题“先猜想、再验证”的过程，进而领悟解决数学问题的方法，提高解决问题的能力.在验证四边形AB′A′B是平行四边形的过程中，学生开动脑筋，各抒己见，教师总结学生的各种方法，帮助学生成功回顾平行四边形的判定方法：两组对边平行（定义）；两组对边相等；一组对边平行且相等；对角线互相平分.教师顺势让学生继续说一说平行四边形的性质有哪些.有了活动探究的铺垫，学生可以很轻松地从边、角、对角线三个角度说出平行四边形的性质.

活动4 如图4，当OA=OB，将等腰△AOB绕着O点旋转180°.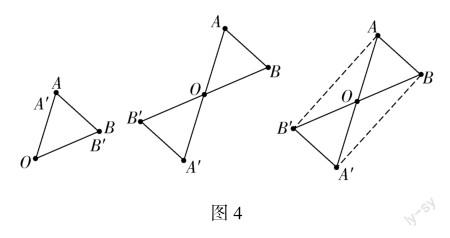

师：将△AOB绕着O点旋转180°之后，连接AB′，A′B，得到的是什么图形？说明理由.

生1：由活动3，得到四边形AB′A′B是平行四边形，对角线相等的平行四边形是矩形.

生2：∠OAB′=∠OB′A，∠OAB=∠OBA，∠B′AB=∠OAB′+∠OAB=90°，有一个角为直角的平行四边形是矩形.

生3：同样的方法，可以得到∠B′AB=∠AB′A′=∠ABA′=90°，三个角都是直角的四边形是矩形.

教师总结学生回答中的矩形的判定方法，并提出问题“矩形有哪些性质呢？”

教学说明：活动4是活动3的特殊情况，旋转特殊的三角形（等腰三角形）180°.学生积极思考，教师给予适当引导，学生用矩形的判定方法证明猜测的结论，最后说出矩形的性质有哪些.

活动5 当∠AOB=90°，将直角△AOB绕着O点旋转180°，得到的是什么图形呢？

教学说明：活动5是活动3的特殊情形，旋转特殊的三角形（直角三角形）180°.由活动3的结论，学生可以得出这个四边形是平行四边形，利用问题中的条件，学生可以给出：AA′⊥BB′，对角线互相垂直的平行四边形是菱形；通过全等或中垂线的性质定理可得AB=A′B=A′B′=AB′，四条边相等的平行四边形是菱形；AB=A′B一组邻边相等的平行四边形是菱形.

活动6 将怎样的三角形按照这种方式旋转可以得到正方形？说明理由.

教学说明：活动4、活动5分别通过旋转等腰三角形、直角三角形研究了矩形、菱形，有了这种研究特殊平行四边形的经验，学生容易联想到旋转等腰直角三角形.学生各抒己见，说明所得图形为什么是正方形，总结回忆正方形的判定方法：一组邻边相等且一个角为直角的平行四边形（定义）；一个角为直角的菱形；一组邻边相等的矩形.正方形可看作由等腰直角三角形绕直角顶点旋转180°形成，此时学生可以完整地描述出正方形的性质：四边相等、对边平行；四个角为直角；对角线相等且互相垂直平分.

环节二：例题精选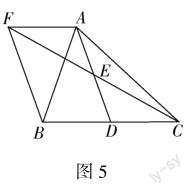

例1 如图5，在△ABC中，AD是BC边上的中线，E是AD的中点，过点A作BC的平行线交CE的延长线于点F，连接BF.

（1）求证：四边形ADBF是平行四边形.

（2）探究填空：

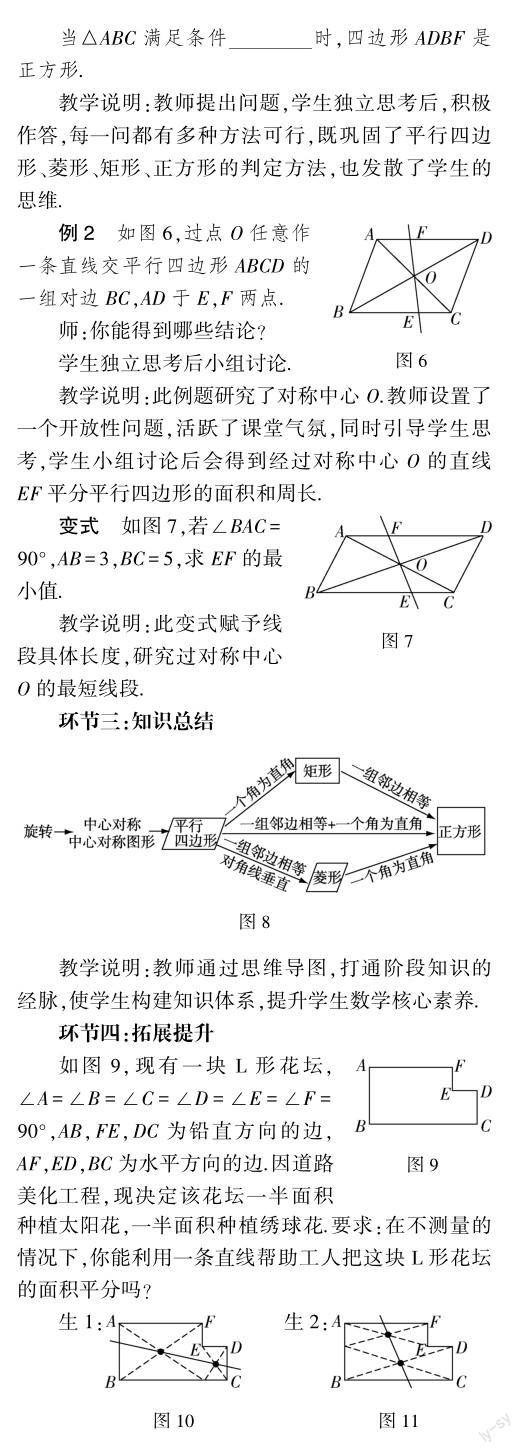
师：以后我们还会学习其他的中心对称图形，比如正六边形、正八边形、正十二边形……当正多边形的边数不断增加时，它的形状无限地趋近一个圆.一个点绕着另一个点旋转360°形成的轨迹就是我们今后要学习的圆（教师用圆规演示，画一个圆）.

教学说明：展望未来的学习之路，为以后正多边形、圆的教学内容做铺垫.教师提出“圆也是由旋转得到的”，揭示了數学研究的重要方法———旋转的重要性.

三、反思教学，提升素养

1.设置活动串，引领学生有效思考.

复习课可以尝试设置活动串，环环相扣，层层推进，使课堂高效紧凑，充分发挥学生的主体性.

2.复习课不是习题课，例题在精不在多.

例题应选择具有代表性的问题，最好能够一题多解，在思考的过程中培养学生的创新能力和思维能力.

3.复习课应实现从知识本位到素养本位.

复习课要以学生为主体，让学生能自我探究，主动揭示知识之间的联系.课堂要沿“认知线”梳理知识，把知识、方法、思想纳入一个系统内，进行整合融通.

【参考文献】

[1]钟鸣，张泉.后建构课堂的章尾复习课设计：以“中心对称图形：平行四边形”为例[J].初中生世界，2021（16）：38-42.

[2]蔡立东.《义务教育数学课程标准（2022版）》：注重核心素养的关联，强调“三会”能力[J].招生考试通讯（中考版），2022（9）：15-18.

[3]陈荣，胡加玉.基于故事情境的数学微课设计与实施[J].小学教学参考，2023（2）：30-33.

[4]李艳荣.思维导图在初中数学复习课中的合理应用[J].数学学习与研究，2022（34）：29-31.