小学数学教学中创造性思维能力的培养

蒋国红

[摘  要] 在小学数学教学中培养学生的创造性思维能力，需要紧紧围绕思维这一本质来设计所要探讨的具体数学问题，要引導学生学会借助数形结合思想和方式来思考，要统筹培养学生的发散性思维和聚合性思维，要注重从日常积累中启发培养学生的创造灵感，更要鼓励学生质疑，营造一种真诚、和谐的课堂氛围。

[关键词] 小学数学;创造性思维;数形结合;灵感;质疑

创造性思维是一种具有开创性意义的思维活动，是个体在问题解决过程中萌生的一种有自己特点的带有创造性见解的思维。在小学数学教学中渗透创造性思维的培养，既是为了改善学生的数学思维品质、提高数学学习能力，也是为了培养学生敢于并善于创新的个性品质。

一、围绕思维，预先设想

创造性思维并不一定是为了创造发明。对于学生来说，能进行改造，有一些新思想、新观念、新方法就可以称得上创造。为此，教师应设计好可供学生观察、试验、猜想与找规律的练习，事先把核心问题从偶然现象中剥离出来。这样学生才能经历一个由现象到本质、由模仿到创新的学习过程。比如对于“如何画一条直线把一个平行四边形分成面积相同的两半”这一问题，笔者设计了以下三步：

第一步，初步思考。大部分学生会想到“连接平行四边形对边的中点和画平行四边形的对角线”的方法，得到四种答案。这一步主要是激发学生初步的发散性思维，学会在模仿中增加可行方案。

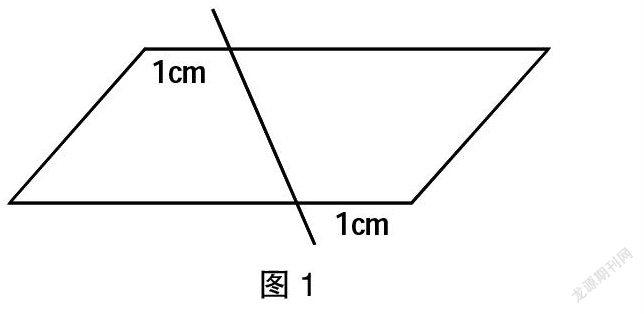
第二步，变化思考。改进解答方向，此时有学生可能会画出如图1所示的直线，于是可引导学生进一步发散思维得到：还可以在纵向的那组对边上画直线，也可以将截取的长度（如图1中的1cm）改为其他相同的长度。

第三步，深入思考。这种直线会有多少条呢？能不能找到一种更科学的画线方法呢？有不少学生会意外发现到，刚才所画的直线全都经过平行四边形对角线的交点。由此猜想：只要经过对角线交点画直线，都能将平行四边形分成面积相同的两半。然后通过画图、比较、计算与论证，最终认定猜想是正确的，得出了问题解决的本质性方案。

二、数形结合，善于构想

低年级学生的数学思维以形象思维为主，中高年级逐步向逻辑思维为主转变。培养学生的创造性思维离不开直观教学，数形结合既是一种数学思想，也是创新思维训练不可逾越的一个阶段。

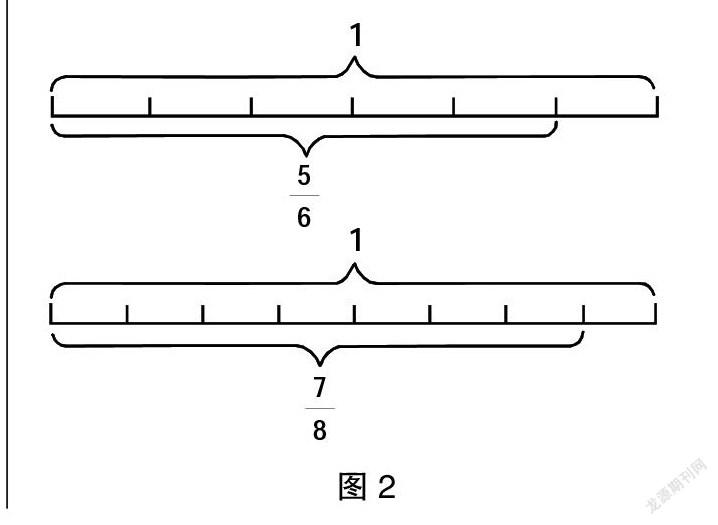
比如比较与的大小，大多数学生会把它们化成同分母或同分子进行比较，也有学生尝试通过化为小数来比较，个别学生还会想到把这两个分数化为由1减去另一个分数的结果来进行比较，这就是一种创造性思维。但学生这样去思考需要经历同分母分数大小比较与减法转换两种过程，思维跳跃比较大，许多学生难以接受，此时若让学生通过画图来进行思考就易于理解了（如图2所示），实现了形象思维向抽象思维的过渡，使创造性思维展现的过程更加完整，理解也会更到位。

三、一字开花，多方联想

发散性思维是进行创造性思维的重要条件。发散性思维是指大脑在思维时呈现的一种扩散状态的思维模式。“一题多解”是培养学生发散性思维的重要途径。为此，教师要为学生营造足够的思考空间，让学生从不同的角度去寻求问题解决的方案，从而呈现“一字开花”的美丽结局。

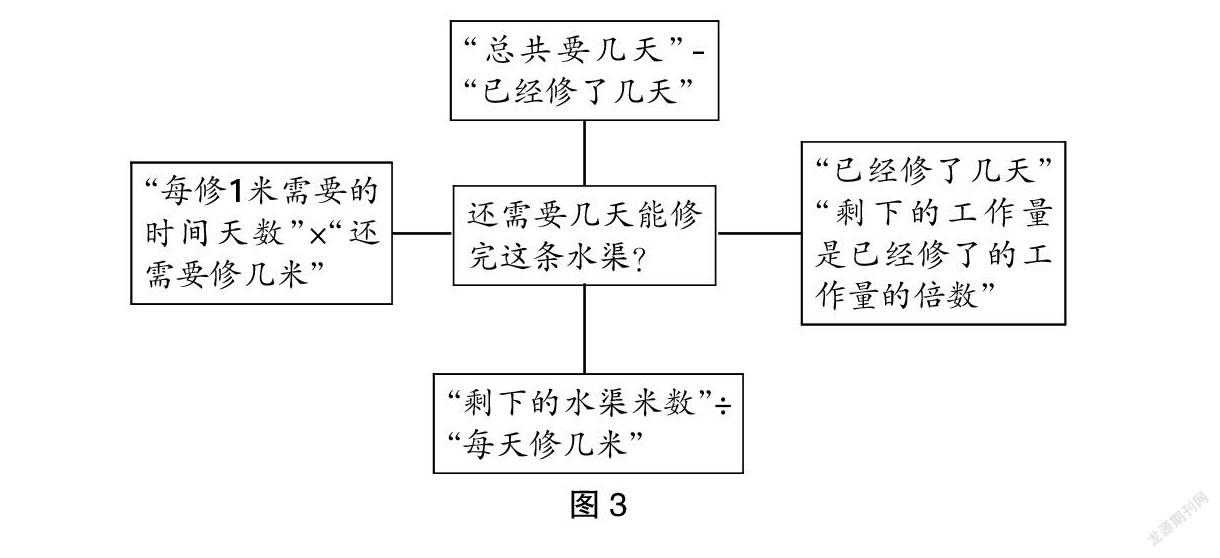
比如有这样一道题：某建筑公司要修一条320米长的水渠，前3天修了120米，那么照这样的速度还需要几天能修完这条水渠？学生可能只会列出如下的算式：（1）320÷（120÷3）-3;（2）（320-120）÷（120÷3）。此时教师不要过早做评价，可以进一步引导：除了从天数出发做减法、从剩下的工作量出发做除法外，我们还可以怎样计算余下的天数？围绕“前3天修了120米”，除了可以计算“每天修几米”外，还可以计算什么？剩下的天数与前边的3天大约是几倍关系？经过师生共同讨论，最后就形成了如图3所示的思维导图，并得出创新的解答方法：（3）3÷120×（320-120）;（4）3÷120×320-3;（5）3×（320÷120）-3;（6）3×[（320-120）÷120]。

四、正反结合，殊途同想

聚合思维也叫求同思维，指的是思考问题时把各种信息聚合起来，向着特定的方向找到一个规律性的答案。聚合思维与发散性思维有着相反的方向，但都可以使创造性思维更加完美。比如对于梯形面积公式的推导，教师一般会引导学生把梯形面积分别转化成熟悉的平行四边形面积、三角形面积进行思考，这属于发散性思维。得出梯形面积公式后，教师会强调这几种面积公式的区别，并再深入思考：梯形面积公式能否演变成后二者（平行四边形和三角形）的面积公式呢？学生通过探究可以发现：当梯形的上下底长度变化到相等时，梯形就变成了平行四边形，此时上下底之和的一半就是平行四边形的底，两个面积公式就是一致的;当梯形的上底缩小到零时，梯形就变成了三角形，下底就是三角形的底，梯形的面积公式也就随之变成了三角形的面积公式。这样通过正反两个方向的结合研究，一方面由发散性思维使课堂充满灵气，结果具有多样性;另一方面又由聚合性思维使多种图形的面积相互关联起来，实现了“殊途同想”。这使课堂充盈着理性，结果具有通透性。

五、激发灵感，萌生奇想

恩·斯图加特说：“直觉是真正的数学家赖以生存的东西。”尽管创造性思维一般意义上都属于逻辑思维，但也离不开直觉思维。直觉思维是指对一个问题没有经过逐步的深入分析，仅根据个人内在的一些感知作出判断与设想，突然对问题产生灵感，从而形成顿悟。小学生在数学问题解决过程中也经常表现出了直觉思维的参与。比如有这么一道题：原计划用15小时看一本360页的小说书，实际每小时比原计划多看了，那么实际多少时间可看完？多数学生列的算式是360÷360÷15×1+，但有几个学生列的算式是15÷1+，他们觉得这样也能得到正确的结果，但一下子又说不清理由，这就是典型的直觉思维。

为了培养学生的直觉思维，教师在教学过程中应该把学习的主动权还给学生，对于学生的奇思怪想不要过早加以否定，要抓住其中的合理部分给以必要的肯定，细心地呵护学生燃起直觉思维的火花，先让学生“跟着感觉走一回”，然后再把灵感与顿悟升华到相对严格的逻辑思维，做出合理的表述。

六、享受过程，民主畅想

课堂是创新思维能力培养的主战场，教师要创设民主、平等的教学氛围，引导学生在探究中享受创新，在创新中学会畅想。比如有这样一道题：某建筑队修一条柏油路，计划每天修35米，8天修完。若需提前1天修完，平均每天比计划多修几米？以下是师生对话：

生1：我列式为35×8÷（8-1）-35=280÷7-35=5（米）。

生2：我列式为35÷（8-1）=5（米）。我的想法是由于要提前1天修完，那么本来最后1天修的35米就应该平均分给前7天去修了，所以每天多修的正好是5米。（大家对这种简易解法非常感兴趣，但是又弄不懂这样解的理由）

生3：老师，我不同意。按生2的方法，如果我设定提前7天修完，那么35÷（8-7）=35（米），即每天要多修35米，35+35=70（米），即1天只能修70米。

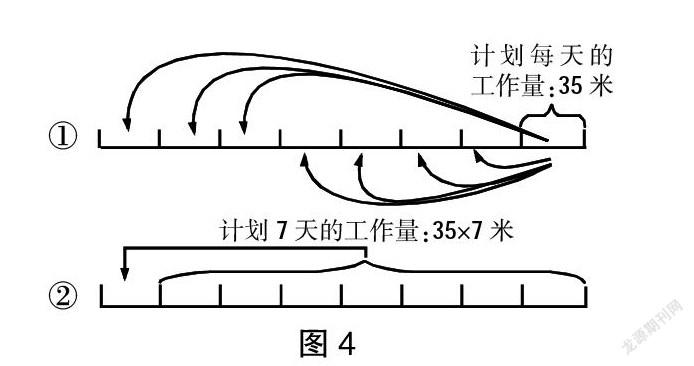
师：我们画个图，结合图形来研究，好吗？（师生共同作图，如图4所示）

生4：生2的解法实际上是35×1÷（8-1），这里把“×1”省略是可以的。

生5：提前7天修完，那么就把7天的工作量35×7=245（米）都加到了1天的工作量中，即35×7+35=280（米）。

在这一教学过程中，学生对生2的做法表示赞赏，但又不太懂这样做的思路，唯独生3大胆提出了疑问。此时教师如果当场否定生3的怀疑，那么生3可能会因此而感觉羞愧，批判性思维的火种也可能由此被扼杀。事实上，生3是在探求“提前x天”的通用方法，这是将问题进一步引向深入的创新精神所在。通过让学生画图探讨，生3很快发现其错怪了生2，能马上理解并写出正确算式，从而获得知识与情感的双重满足。

总之，在小学数学教学中培养学生的创造性思维，需要有一个可供学生拾级而上的解决数学问题的平台，要教给学生科学的思考问题的方法，要全面考虑学生的发散性思维与聚合性思维，要兼顾逻辑思维、形象思维与直觉思维，同时教师要鼓励学生积极质疑，营造真诚和谐的、有助创新的课堂氛围。

3883500559548