巧用操作活动积累数学基本活动经验

毛丽

[摘  要] 巧用操作活动直观引导学生学习数学，可以正确地建立新知的表象，进而实现思维的可持续发展，积累数学基本活動经验。鉴于此，教师需组织好各种操作活动，引导学生在操作的过程中经历、体验和品味，真正地从亲身经历走向“经验”，从而积累有效的数学基本活动经验。

[关键词] 操作活动;活动经验;积累

著名教育家陶行知曾做过这样一个比喻：我们要有自己的经验做“根”，以这经验所发生的知识做“枝”，然后别人的知识才能接得上去，别人的知识才能成为我们知识有机体的一部分。由此可见，活动经验的获取和积累有赖于学习者丰富的活动体验，要想让经验的“根”生长得更深，只有让学习者在亲身经历中获得切实的体验，才能不断地积淀活动经验，形成能力。操作活动作为一种特殊的认识活动，可以直观引导学生学习数学，正确建立新知的表象，深刻理解知识的本质，进而实现思维的可持续发展。本章以教学实践中引导学生有效性的操作活动为专题，进而通过经验的生长实现思维的发展而做一些探讨。

一、聚焦探索性操作活动，让活动经验得以生长

教育心理学研究显示，儿童的思维发展是一个循序渐进的过程，一般情况下是由操作水平逐步过渡到表象水平，再向着分析水平发展。事实上，深入分析儿童思维的发展过程，可以发现其刚好与认知发展阶段相吻合。因此，课堂中教师要以思维发展过程为依据，创设合理而有效的问题情境，引导学生开展探究性操作活动，使其快速建立表象，在自然经历思维转化的过程中发展思维，生长经验。

案例1：长方形和正方形的认识。

活动1：教师通过PPT出示本校的部分场景图，让学生从中寻找已学的基本图形，并思考“长方形有哪些？正方形有哪些？你判断的依据是什么？从中你知道了哪些知识？”

活动2：将课前准备好的长方形取出，借助于看和摸两种方法，并对比PPT中呈现的长方形，思考“它们有何相同点？”

活动3：借助于手边的工具，验证以上活动2中的发现。

师：通过刚才的一系列操作和交流，大家一定形成了深刻的认识。那么，下面就请一些同学来汇报一下自身的操作过程。（学生跃跃欲试，七嘴八舌地说出了自身的一些体验）

师：那么，在刚才的活动3中，大家是如何验证长方形的4个角为直角的？

生1：我是用三角板上的直角进行比对的。

师：不错的想法，那就请你来示范一下。（生1板展，其他同学观看）

师：这个方法需要反反复复地测量，其他同学也是运用的这个方法吗？是否有更加简便的方法？

生2：还可以这样对折。（生2拿起长方形纸片开始对折）

师：在生2的演示中，我们可以发现这个长方形的4个直角重合成了一个角，那的确是简便多了。我们一起再来观察一次，之后再动手试一试。（学生观察PPT的演示，之后再动手练习）

……

倘若教师直接给出图形，并生硬地抛出定义，由于缺少感受知识发展的过程，易造成无法透彻理解而快速遗忘的典型问题;而从图形的特征出发，让学生通过动手操作，亲自归纳图形的特征，既有助于对图形的深入理解，又可以培养学生归纳、概括的经验。以上活动中，教师花了大量篇幅让学生自主去发现长方形角的特征。学生通过多感官的参与，很快得出猜想和发现，并积极主动地想方设法验证自身的猜想，最终在大家的通力合作下得出结论。这样的探究性操作，让学生亲自去动手，让学生亲身经历过程，让熟悉的场景和信手拈来的操作材料成为学生学习新知的重要工具。在一个又一个的动态场景中，学生初步建构了自己脑海中长方形和正方形的模型，再通过看、摸、量、比、折等多个操作方法，使其获得真切的体验，积累了经验和方法，体现了数学思考的优化过程，更重要的是激励了学生自主探索和感受到了数学魅力。

二、立足体验性操作活动，让活动经验得以充实

经历和体验可以帮助学生快速获得经验，从而学生完整参与数学活动十分重要。因此，在一些概念、定义或公式的教学中，教师应有效链接学生已有的经验和教学内容，设计体验性操作活动，让学生亲历数学知识、数学思想的产生、创造和应用的过程，有效沟通学生的实践操作、数学语言和数学思维，则可以在感性逐步上升到理性的过程中充实活动经验。

案例2：分米和毫米。

活动1：取出一根1分米的小棒，用手握一握，摊开手掌感受一下;再放下小棒，记住1分米在手指间的距离;最后闭眼回忆1分米到底有多长。

活动2：伸出手比画1分米的长度，再取出小棒进行验证。

活动3：分小组活动，找寻日常生活中1分米长的物体。（教师事先在教室的多处布置好一些物品，如磁带盒、药品盒等）

活动4：教师取出一个装着彩带的盒子。首先，教师拉出1分米长，学生观察后拿掉，让学生对1分米形成认识;接着，教师继续将彩带往外拉出一段，请学生交流并判断“这一段是否是1分米”;最后，师生共同验证。在此之后，教师又分别拉出4分米、6分米、10分米长度的彩带，让学生猜一猜长度，最终再进行验证。

活动5：观察米尺，并猜想1米和10分米的关系，再进行验证。

亲身体验是获得活动经验的主要手段，直接关系到学生所获经验的完整性和有效性。以上活动是笔者基于学生基本活动经验的积累而设计的，活动的素材来源于学生的日常生活，活动也是基于学生的喜闻乐见而设计的。整个活动过程，学生经历了从独立操作过渡到合作操作的过程，从初步感知到建立表象，再在丰富的感性经验中使得“认识1分米”的经验逐步充实，最终建构分米与米之间的联系，形成深刻的认识。这样的活动过程是具体的、形象的，同时也是充满数学味的，让学生水到渠成地强化数学经验，使得创造性和自主性均得到了提高。

三、开展拓展性操作活动，让活动经验得以提升

教育是自然生长的过程，这个过程并非通过灌输而实现的被动过程，而是经验改组或改造的生长过程，更应该是在思考和体验的过程中发展。为此，教师只有在新知应用环节中积极开展扩展性操作过程，引导学生观察、操作、比较、联想、归纳，才能拓宽学生的思路，使得原本单薄的经验逐步丰厚，达到积累和提升的目的。

案例3：倍的认识。

操作活动：涂色游戏。

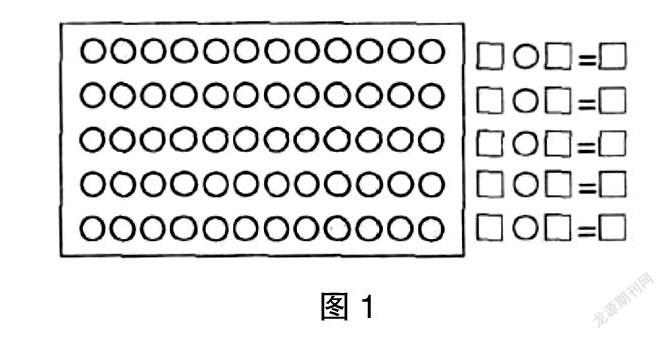
师：下面，请大家用彩笔在圆圈内完成涂色（如图1所示）。（教师来回巡视，学生认真涂色）

师：下面请观察自己的作品，未涂色部分是涂色部分的几倍？（学生展开自主探究，教师发现典型案例）下面，请生3和生4来展示一下他们的涂色。

生3：第一行有2个涂色、10个未涂色，所以未涂色是涂色的5倍;第二行有5个涂色、7个未涂色……（由于思维卡壳，生3不知如何表达是好）

生4：第一行有1个涂色、11个未涂色，所以未涂色是涂色的11倍;第二行有2个涂色、10个未涂色，所以未涂色是涂色的5倍;第三行有3个涂色、9个未涂色，所以未涂色是涂色的3倍;第四行有4个涂色、8个未涂色，所以未涂色是涂色的2倍;第五行如果有5个涂色、7个未涂色，所得的算式有余数;但第五行如果有6个涂色、6个未涂色，未涂色是涂色的1倍。据此得出以下算式：11÷1=11，10÷2=5……

一系列的教学实践表明，只有在操作中亲身经历并积累了这样的活动经验，学生在今后的数学学习中才能更好地应用。以上案例中，教师精心设计拓展性问题，组织开放的探究活动，为学生提供自主探索和自由发挥的时间和空间。整个操作活动，学生不仅加深了对“倍”的理解和认识，体验了多感官协同参与的有效性，更重要的是通过不断地探索和顿悟，使得学生获得了有序思维问题的经验，累积了丰富和科学的探究性经验。

总之，学生基本活动经验的积累需要教师精心设计探索性操作活动、体验性操作活动和拓展性操作活动，引导学生自主经历、体验和品味，从而提升数学活动经验，最大限度地促进经验的生长，实现思维的可持续发展，让数学课堂真正走向实效。

3072500559581