年龄差不变

陈慧

[摘  要] 将差为一定值的两个数作为题中的一个条件，这种应用题被称为“年龄问题”。文章从网课教学中学生连麦不积极这个现状出发，深刻分析学生在解答“年龄问题”时遇到的障碍，谈谈在解决“年龄问题”时所用到的一些策略。

[关键词] 年龄差;网课;策略

“年龄问题”是人教版小学数学阶段重要的内容之一，它往往与和差、和倍、差倍等问题有着密切联系。在最近的网课教学过程中，笔者碰到了一个问题，觉得其有一定的探究价值。

【案例描述】

在练习阶段，笔者让学生尝试解决一个问题：“今年父亲的年龄是儿子年龄的4倍，20年后父亲的年龄是儿子年龄的2倍，今年儿子多少岁？”

许多学生虽然知道父与子前后的年龄都存在倍数关系，但是对于将今年的和20年以后的两个倍数条件如何联系起来表现得手足无措。笔者问“有没有同学来连麦回答”时，学生鸦雀无声，无人作答。

为什么以往连麦积极的学生也没有动静呢？在交流之后发现，绝大多数学生反映无法找到父与子的年龄差，不知如何作答。

【案例剖析】

为什么学生会产生这种解题障碍呢？针对年龄问题可以进行以下剖析：首先年龄问题是现实中存在的问题，比如父亲今年35岁，儿子今年5岁，父亲比儿子大了30岁。考虑现实问题的时候，学生会不自觉地去比较自己和自己的父亲之间的年龄差，而不会去关注父亲的年龄是自己的几倍。其次，当现实中的年龄被放进高段数学教材后，绝大多数教学和习题更加侧重于倍数关系，比如父亲今年35岁，儿子今年5岁，父亲的年龄是儿子的7倍。根据学生抽象性思维发展的阶段特征和对知识综合运用的要求，这类题往往会让学生的注意力放在“倍数”上，忽视现实中习以为常的“年龄差”，因此在解决这类问题时，学生无法找到解题的突破口。为了能够将生活常识和数学知识相结合，帮助学生了解年龄问题在生活和数学上的联系，掌握差倍问题的实际应用，笔者做了如下思考。

【问题解决策略】

年龄问题是一种典型的差倍问题，也是一种综合性较高的问题类型，可以引入方程思想来解决。在实际教学中，学生无法正确处理解决年龄问题的关键，同时线上教学师生之间沟通效率低、交流效果差，使得这个问题不能顺利解决，离教学目标有所差距。经过思考，结合网课教学的现实，笔者觉得可以从三方面来制定教学策略。

策略1：问题与现实结合

数学教学中的合作交流不能等同于日常随意性的谈话，它应具有一定的学习目标指向性，是为解决某个具体的问题而进行的合作与交流。加之线上教学对于课堂的实时交流造成了阻碍，因此在目前的网课教学中，如何引导学生解题便成为重中之重。这需要教师引导得法，在提出问题之后教师紧接着询问学生解题是否有困难，不让他们产生“根本无从下手”的无力感。当被询问是否有困难时，大多数学生往往会从紧张的情绪中解放出来，坦然地向教师提出疑惑。学生有了交流的欲望后，教师就可以抓住契机，对学生进行引导，利用现实中的例子，将学生的注意力由倍数关系引向年龄差，帮助学生抓住解决年龄问题的关键。

案例（截取片段）

师：我们来想一想，自己的爸爸今年几岁，你今年几岁呢？你和爸爸之间今年差几岁呢？

（学生连麦回答。）

师：那2年之后，你的爸爸变成了几岁？你几岁呢？这时候你和爸爸之间又相差了几岁？

（学生连麦回答。）

师：那么请问，今年你和爸爸的年龄差与2年之后你和爸爸的年龄差一样吗？

（学生回答一样。）

……

让学生以自己的亲身经历来提炼抽象冰冷的数学问题中的关键点，由此可以生动得将“年龄差不变”这个核心植入学生的脑海，之后反复展现这个过程，加深他们对“年龄差不变”的印象。

策略2：知识与知识串联

在学生通过现实中的例子了解了“年龄差不变”这个核心并对此有了深刻印象之后，教师需要唤醒学生的先前记忆，促使他们在解题时使用画线段图的知识，以达到融会贯通的解题效果。图形结合使抽象的数学问题变得直观，学生应好好掌握这一解题策略。

利用图形结合策略，这一问题会有两种使用线段图的方式。

第一种类型中，已知n年前后父与子的年龄倍数关系，求解父與子n年前或n年后的年龄。

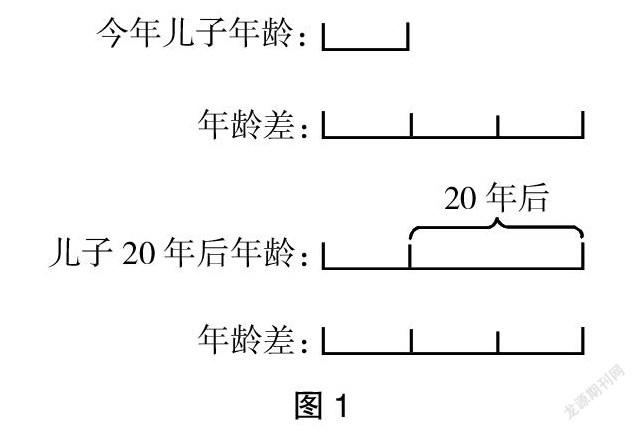
例：今年父亲的年龄是儿子年龄的4倍，20年后父亲的年龄是儿子年龄的2倍，今年儿子多少岁？

师：这里，我们知道了今年和20年后父与子年龄的倍数关系，怎么求儿子今年的年龄？

（预设1：学生提出用方程的思想来设未知数，自然可以顺利解题;预设2：学生不知道该如何列算式。）

师：大家想想，已知条件有什么？除了告诉我们倍数关系以外，我们所知道的年龄问题的另一个特征是什么？

（学生回答年龄差不变。）

师：是的，题目中父与子的年龄差是不变的，那我们能不能将已知的倍数关系转换成不变的年龄差呢？

（学生连麦分享解题思路。）

（根据学生的思路，结合线段图，把今年儿子年龄看作1份数，今年的年龄差是3份数，那20年后，父亲的年龄是儿子年龄的2倍，即把20年后儿子的年龄看成1份数，年龄差也就是1份数，即年龄差不变，20÷（3-1）=10，即今年儿子的年龄是10岁。）

第二种类型中，已知今年父与子各自的年龄，求解x年后父亲的年龄是儿子的a倍或求解a年后父亲的年龄是儿子的x倍。

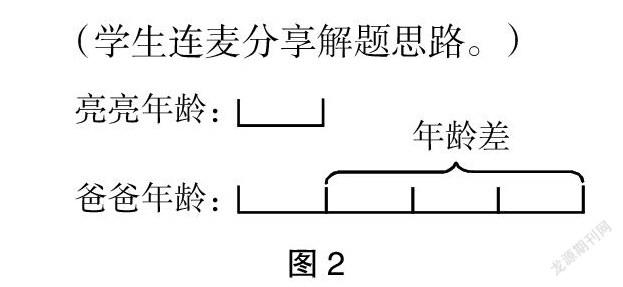
例：爸爸今年37岁，亮亮今年7岁，几年后爸爸的年龄是亮亮的4倍？3年之后爸爸的年龄是亮亮的几倍？

师：在这个问题中大家要注意爸爸今年37岁，亮亮今年7岁，他们二者之间的年龄差是多少？

（学生连麦回答。）

师：如何将不变的年龄差转化成题目中的倍数关系？

（学生连麦分享解题思路。）

师：根据不变的年龄差30和爸爸的年龄是亮亮的4倍这两个条件，我们可以推断出爸爸的年龄比亮亮多出来的3倍就是30，由此求出1份数，即几年后亮亮的年龄。

（利用线段图，爸爸的年龄是亮亮的4倍，爸爸的年龄比亮亮多3倍，又年龄差是30，用30÷3=10，可以知道几年后亮亮的年龄是10，即10-7=3年。）

对于这个问题，教师应该经常提醒学生牢记“年龄差不变”这个关键点，将现实生活中的经验成功转移到数学问题中。

策略3：课堂与课后同步

基于网课教学过程中，直播课无法对学生进行作业面批，课后询问沟通不便，学生答疑解惑较难的现状。教师可以试着将课堂与课后同步，充分发挥学生的主体作用，培养学生的分享意识和集体观念。

（1）视频共享你我他。教师可以就年龄问题的经典例题进行视频录制或者让顺利求解年龄问题的学生将自己的解题思路拍成视频分享给大家。学生课后视频的录制和讲解，让师生之间的联系不再局限于网课直播间的互动。同时教师课后有效的视频指导，为学生巩固了知识要点，检验了课堂的学习效果。学生录制的视频被其他同学点击观看点赞，大大增强了视频录制者学习的自信心，为个人提供了更好的成长空间，同时对集体的责任感和荣誉感会更加强烈。

（2）小小网红一直播。除了录制小视频的方式，教师还可以让学生充分利用家里拥有的网络资源，让部分充分理解年龄问题的学生在教师的指导下开设直播间，当当小网红，在个人的直播间用诙谐的方式和同学面对面的交流，为其他学生学习知识出谋划策。这种方式不仅可以加深学生对年龄问题的印象，而且符合现在的潮流趋势，能让学生对学习更感兴趣、更加投入。

通过对上述案例的反思和剖析，结合网课学习的特点和新型的教学方式，笔者提出以上策略，希望能对以后有效解决年龄问题的相关教学提供帮助。

3768500559561