设计核心问题，发展数学思维

刘玉蓉

[摘  要] 核心问题是培养、发展学生数学思维的重要载体。基于理论研究与教学实践，提出核心问题设计的有效路径，即把握教材和学生，在知识关联处设计核心问题;把握知识本质，在知识重点和难点处设计核心问题;引起思维碰撞，在困惑点和易错点处设计核心问题;提升认识深度，在数学思想渗透处设计核心问题。

[关键词] 核心问题;数学思维;小学数学

数学核心问题是学生思考的聚焦点，也是学生探究的集中点，它指向数学知识本质，需要学生进行深度思考，并在对核心问题的探究过程中达成对知识的深度理解，完成知识的完整建构，发展学生数学思维。核心问题的设计，使得学生超越传统的“一问一答”的对话模式，从浅尝辄止的思考桎梏中解放出来，让学生在收获真知的基础上，增长数学活动经验，发展数学思维。文章基于理论研究与教学实践，提出核心问题设计的有效路径，力图为进一步发挥核心问题在教学中的作用提供一定借鉴和思考。

一、把握教材和学生，在知识关联处设计核心问题

从教材的编排特点看，数学知识具有相互关联性，在逻辑上呈现出螺旋式上升特点。就某一节课而言，知识内容具有一定的独立性，但从整体上看，数学知识则是密切相关的，这就需要教师在设计核心问题时，能够从整体上把握知识之间的内在关联，根据知识的迁移规律，引导学生把新旧知识作为一个整体来认知，使学生厘清知识之间的框架脉络，最终促进数学知识的整体建构。从学生的认知特点看，学生在学习新知之前往往已经积累了一定的知识，教师在设计核心问题时，要善于把握新旧知识的关联性，在学生认知经验的“增长点”处设计核心问题，帮助学生打通新旧知识之间的“关节”，促进学生的认知经验由内向外“自然生长”[1]。

例1  “比例的认识”教学节选

师：同学们，我们已经学习了比例的知识，在上学期我们还学习了比的知识，那么，比和比例有什么异同点呢？

生1：比表示两个数相除;而比例表示两个比相等。

生2：比只有两项，即前项和后项，比如7∶11;而比例却有4项，即两个外项和两个内项，比如，4∶3=8∶6。

师：对，另外，比没有等号，它不是等式;而比例有等号，它是一个等式。那么，比和比例之间有什么关联吗？

生3：比是比例的一部分，比例是由比值相等的比组成的。

师：对，比和比例是两个既相互区别又相互联系的概念，我们在学习和运用的过程中，要注意把握它们的异同点，这样才能更好地理解知识。

“比的認识”和“比例的认识”尽管分别编排在北师大版六年级的上册和下册，但这两个概念无论在形式上还是在本质上都具有内在的关联性。在学习比例知识时，教师立足于新旧知识的内在关联，结合学生已有的认知经验，设计核心问题“比例和比有什么异同点”，引导学生主动建构起新旧知识之间的联系，把握“比”和“比例”之间的内在关联。这一过程实现了知识的整体建构，提升了学生对知识的认知深度，发展了学生的数学思维。

二、把握知识本质，在知识重点和难点处设计核心问题

在数学教学中，教师要通过去粗取精的方式正确把握知识本质，并在此基础上，正确定位知识的重难点，在知识重难点处设计核心问题，引导学生探究、质疑和反思。这样可达到突破重点、分散难点的作用，并最终发展学生数学思维，提升课堂实效。

例2  “分数的意义”教学节选

教学片段1

师：学习分数，最重要的环节就是认识单位“1”，什么是单位“1”呢？我们来看下面的问题。

师：把1根香蕉平均分给2只大象，每只大象分到香蕉数量的几分之几？

生1：。

师：把3根香蕉平均分给2只大象，每只大象分到香蕉数量的几分之几？

生2：。

生3：不对，应该还是。

师：如果我把5根香蕉平均分给2只大象呢？

生3：仍然是。

师：香蕉的数量一直在变，为什么每只大象却还是分到香蕉数量的呢？

生4：单位“1”指的不是一个具体的数字，单位“1”可以是1个香蕉，也可以是很多香蕉。

师：对，单位“1”并非一个固定的数字，它在这里指的是“1个整体”的意思。只要是把单位“1”平均分成2份，每一份就占总数量的。

教学片段2

师：我们应该如何理解“平均分成若干份呢？”

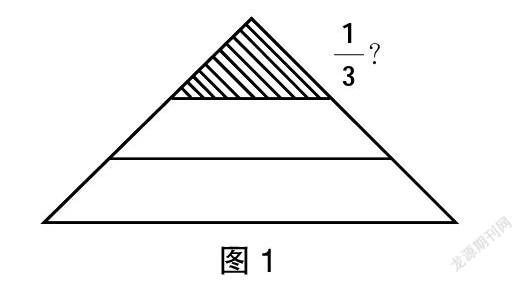
师：这个图形中的阴影部分可以用来表示吗？（如图1）

生：不可以。

师：为什么呢？

生1：这个三角形的确被分成了3份，但是每一份都不一样大，不是“平均分成若干份”。

师：对，正确理解“平均分成若干份”，是理解分数意义的重要环节。

设计核心问题需要教师把握知识本质，从知识本质中剥离出知识重难点，这就要求教师要从整体上把握知识内涵，并对学生的认知规律了然于胸[2]。教学中，教师设计了两个核心问题：什么是单位“1”？如何理解“平均分成若干份”？这正是学生认识“分数的意义”最重要的两个问题，也是学生认知上的难点。教学中，教师要通过引导学生对核心问题进行探究，使学生的认知直达问题本质。如例题中：通过举例和分析的方法使学生深刻认知单位“1”的具体含义，通过画图分析法使学生更准确地理解了“平均分成若干份”的含义等，这样的问题为学生从本质上理解“分数的意义”打下了坚实的根基。

三、引起思维碰撞，在困惑点和易错点处设计核心问题

学生在数学学习中，经常会出现认知上的困惑之处、易错之处。教师在学生认知困惑和易错处设计核心问题，可以引导学生通过自主思考、主动探究，在追根溯源中一步步抽丝剥茧，最终触及问题本质，帮助学生解决认知上的困惑点和易错点，使学生冲破认知障碍，进一步发展学生深刻的数学思维[3]。

例3  “长方体的体积”教学节选

师：请同学们判断“一个边长为6厘米的正方体，它的体积和表面积相等”这句话对吗？

生1：正方体的表面积公式是S=6a2，而正方體的体积公式是V=a3，只需要把6代入公式就可以判断了。

生2：这两个公式算出来的结果都是216，看来这句话是正确的。

生3：对，这句话没有问题。

师：同学们再从细节处考虑一下，表面积和体积能比较大小吗？

生3：哦，我知道了，表面积使用的是面积单位，体积使用的是体积单位，在这道题中，表面积的单位是平方厘米，体积的单位是立方厘米，它们的单位都不一样，根本就不能比较大小。

生1：是呀，这真是特别容易出错的地方，我们都没有发现这一点。

师：我们学习知识一定要严谨，注意把握细节，否则一不小心就会跌入“知识陷阱”。

评析：解决困惑点和易错点是学生学好数学的关键。在教学中，教师设计核心问题，引导学生比较边长为6厘米的正方体的表面积和体积的大小。通过探析和辩论，引发了学生的思维冲突，有一部分学生对此题的正确性深信不疑，却忽略了表面积和体积在单位上的本质不同。通过对本题的解析，不但使学生辨清了表面积和体积的本质区别，还培养了学生严谨的数学思维。

四、提升认识深度，在数学思想渗透处设计核心问题

数学思想是数学知识的本质和灵魂。弗里德曼认为：“数学思想是数学逻辑结构最重要的载体。”在数学思想渗透处设计核心问题，能够使学生在解决问题的同时领悟数学思想方法，能够优化学生的数学思维结构，提升学生数学思维品质，使学生在解决问题过程中做到举一反三、融会贯通。

比如，在讲到“三角形的面积”时，教师提出问题：“上节课，通过把平行四边形转化成长方形，最终推导出了出平行四边形面积公式。据此猜想一下，我们应该怎样推导三角形面积呢？”学生自然地想到把三角形也转化成我们学过的图形。教师进一步提问：“那应该把三角形转化成什么图形呢？”学生讨论，意见不一，有的学生认为可以试着把两个三角形拼成长方形，有的学生则认为应该把两个三角形拼成平行四边形。在此基础上，教师引导学生展开探究活动，最终，学生通过把两个完全相同的三角形拼成平行四边形的方式推导出三角形面积公式。

教学中，教师通过设计核心问题，向学生渗透了转化的数学思想，使学生在解决问题的同时，掌握了数学思想方法，从而增强了学生的认知深度，提升了学生的数学思维品质。

在教学实践中，教师要注重发挥核心问题的引领作用，通过设计核心问题引导学生高效率地开展数学思考和数学探索，深度理解数学知识。通过对核心问题的探索，感悟数学知识本质，优化数学思维品质，提高学生数学素养。

参考文献：

[1]  梁兰. 以核心问题为基点促进深度学习[J]. 广西教育，2020（21）.

[2]  谢敏，赖玉娟. 探讨“核心问题”引领数学课堂教学的实践策略[J]. 数学教学通讯，2020（07）.

[3]  郑毓信. 用案例说话：数学教学中“核心问题”的提炼与“再加工”（二）[J]. 小学数学教师，2018（09）.

3089501908246