模型思想在数学概念教学中的应用

于江兵

[摘 要]数学课程标准强调发展学生的模型思想。模型思想的建立对数学概念的建立起着重要作用。概念教学与模型思想的形成是一致的，概念中模型思想的建立重在经历获取新知识的能力和过程，而不是概念的结论。

[关键词]数学建模;模型思想;概念教学

[中图分类号] G623.5 [文献标识码] A [文章编号] 1007-9068（2021）35-0054-03

数学课程标准中明确指出，应当注重发展学生的模型思想。数学建模是一种数学思想方法，模型思想的建立对数学概念的建立起着重要作用。数学建模的过程分为四个环节，即表述、求解、解释、验证，这四个环节在概念教学中可以与教学环节一一对应，也就可以理解为数学建模的过程实质上就是数学概念形成的过程。下面笔者从教材的编写和实际教学两个角度来分析模型思想在数学概念教学中的应用。

一、教材概念教学编写意图与模型思想形成的分析

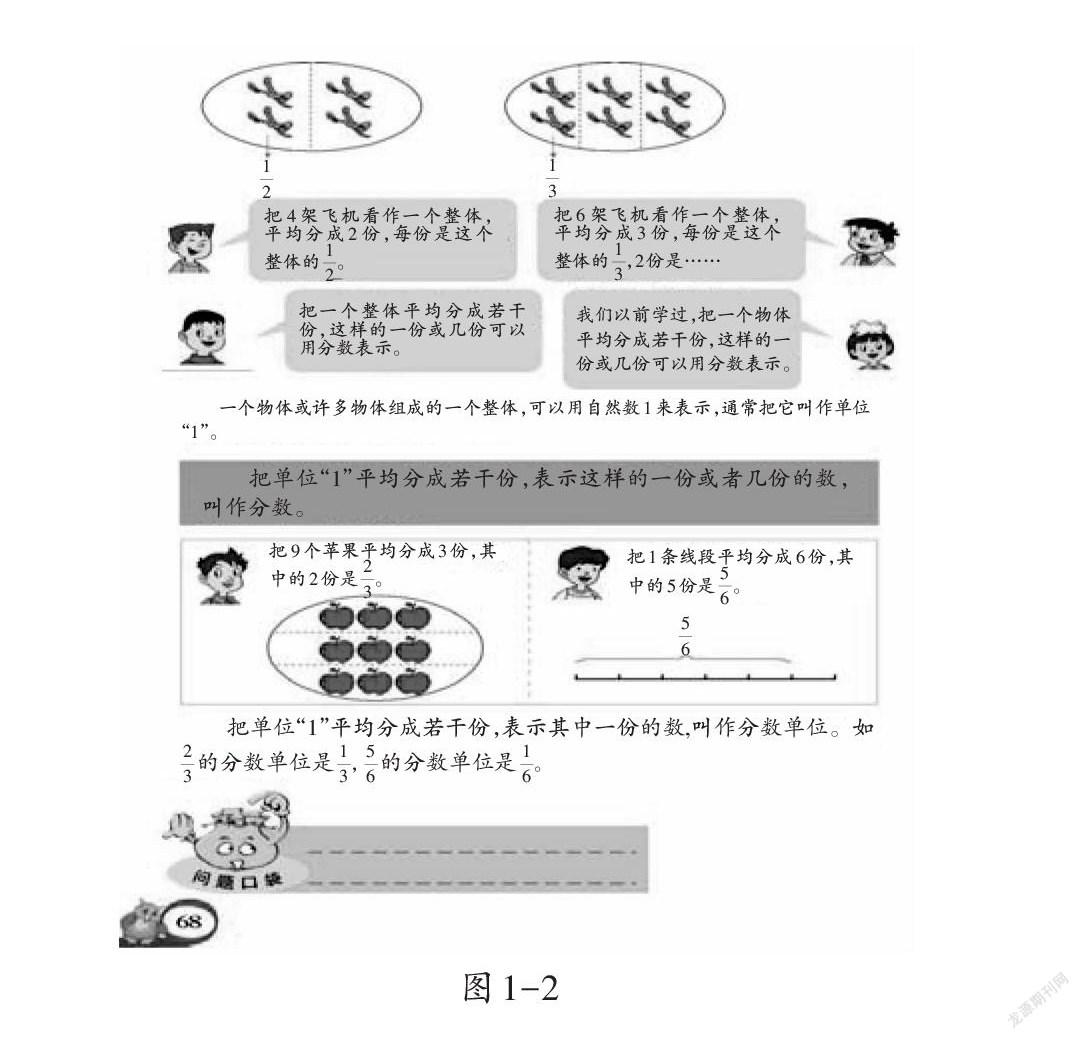
教材概念教学的编写主要遵循数学建模的四个环节。以青岛版教材五年级下册“分数的意义”为例，教材在呈现情境图（如图1-1和图1-2）之后，让学生根据情境提出数学问题，这就是一个表述和求解的过程，这节课要求解的问题比较多，有单位“1”、分数单位及分数的意义等问题。

“分数的意义”是一节典型的概念课，从教材的编写意图来看，它从数学建模的四个环节来体现概念的形成。比如教材对于单位“1”概念的建立，为了让学生建立起单位“1”的模型，教材在设计单位“1”教学内容时，结合了学生的生活实际，用5个船模、4个和6个飞机模型等素材建构了单位“1”的模型。教材抓住了单位“1”的固有特征，即单位“1”就是一个物体或一些物体组成的一个整体。教材在帮助学生建立单位“1”的概念时，先引导学生从5个船模入手形成一个整体的概念（这就是对模型的一个表述过程），在学生有了一个整体的概念后，再用4个和6个飞机模型帮助学生总结出单位“1”的概念模型（这就是对模型的解释过程）。最后通过调查、收集数据，观察和研究概念所固有的特征和内在规律，抓住概念的本质属性，帮助学生建立概念的模型（这就是一个验证的过程）。

二、将教学流程与模型思想融合应用

从数学课程标准和教材的编写意图来看，概念教学也应围绕数学建模的四个环节来开展。下面以“建立单位‘1’”概念为例谈谈如何实施应用。

师：我们从5块巧克力中找到了[15]，那么你能找到10颗棋子的[15]吗？请以小组为单位，利用手中的学具找一找，把你的想法与小组同学说一说。

（小组活动，派代表上台汇报展示。）

生1：把10颗棋子看成一个整体，平均分成5份，其中的一份就是[15]。

（教师引导学生用笔圈出一个整体，平均分一分。）

师（课件演示将5块巧克力、10颗棋子圈出后平均分成5份的过程。）：我们把5块巧克力、 10颗棋子等物体都看成一个整体，平均分成5份，其中的一份就是[15]。

师：仔细观察这两幅图（图略），你有什么发现？把你的发现和同桌说一说。

生2：都用[15]来表示。

生3：每份的数量不一样。

师：为什么每份的数量不一样，而却都可以用[15]表示呢？

生4：都平均分成5份。

生5：每个整体的数量都不一样。

生6：都是把一个整体平均分成5份，取其中的一份，所以是[15]。

师：因为被看成整体的数量是不一样的，所以每份的数量不一样。

师：刚才我们从5块巧克力和10颗棋子中找到了[15]，想不想再从其他物体中找出不同的分数？

师：你能从4根小棒中找到[12]吗？与同桌一起动手摆一摆小棒。

（学生上台展示找到的[12]，教师引导学生边圈出一个整体边说“分”的过程。）

师：你能从6根小棒中找到[13]吗？与同桌一起动手摆一摆小棒。

（学生上台展示找到的[13]，独立完成边圈出一个整体边说“分”的过程。）

……

师：你能举例说明什么是单位“1”吗？

上述教学大致分成了四个环节，即创设情境、提供素材;分析素材，理解概念;借助素材，总结概念;巩固拓展，应用概念。这四个环节与数学建模的四个环节一一对应。

1.创设情境，提供素材（表述）。在教學中教师为学生提供学具，让学生找[15]，学生在找的过程中产生了探索解决问题的热情，为概念的形成奠定了基础，引发了学生对单位“1”概念的形成的初步探索。

2.分析素材，理解概念（求解）。教师提供多种不同的素材给学生操作，并且注重了操作方法的指导。在学生操作演示过程中，教师始终指导学生圈一圈、分一分、找一找。“圈”是指圈出单位“1”，“分”是指平均分，“找”是指找出单位“1”的几份即分数。“圈”就是学生建构单位“1”的过程，学生进行“圈”“分”“找”的过程就是把单位“1”平均分成若干份，表示其中一份或几份的过程，即建构分数概念的过程。学生通过这样的操作，不仅理解了单位“1”，更体会到了分数概念的形成过程。

3.借助素材，总结概念（解释）。这节课教师给学生提供了不同的素材，让学生自主验证，学生在经历了自主操作和验证之后总结出了概念。

4.巩固拓展，应用概念（验证）。教师最后让学生找一找生活中的单位“1”，是对这一概念进一步的巩固和应用。在经历“教师的指导操作—学生的尝试操作—学生的独立操作”这样的活动之后，学生逐步在头脑中建立起了分数的概念，完成了对分数模型的建构。

三、概念教学建模过程中要注意的问题

1. 要创设具体的情境，激发学生的探究兴趣。由于受年龄、知识和生活经验的限制，学生以具体形象思维为主，而数学概念是比较抽象的。因此，在数学概念教学中教师要从学生身边所熟悉的情境入手，通过创设具体的情境逐渐引入概念的抽象过程，从而激发学生的探究兴趣。

2.要关注概念模型形成过程的教学。概念教学中模型思想建立的重点是创设情境引导学生解决问题，而不是简单地得出概念。因此，教师应该注重过程，加强操作，让学生经历概念形成的过程，让学生在实践中学会学习。教师还要重视操作方法的指导，提高操作训练的有效性。学生经历了正确的操作活动之后，也就经历了概念形成的过程，同时完成了数学模型的建构。

3.要注重加强对近似概念的辨析。在小学数学中，虽然很多概念的含义接近，但本质上是有区别的，对于这类学生容易混淆的概念，教师要注重引导学生对它们进行辨析比较。通过辨析找出近似概念之间的相同点和不同点，这样既能培养学生对易混概念自觉进行比较的习惯，也能提高学生理解概念的能力。

4.要关注概念教学中学生迁移能力的培养。数学中的很多新概念与旧概念都有着内在联系。在教学中教师要培养学生知识迁移的能力，让学生学会充分运用旧概念来引出新概念。利用学生已掌握的旧概念讲授新概念，学生比较容易接受。把旧概念作为学习新的基础，以旧引新，再化新为旧，这样循环往复，既能促使学生理解概念，又能让学生有效掌握新旧概念间的联系和区别。

5.要抓住概念的本质属性来理解概念。概念是对事物本质属性的概括，学生理解概念的过程就是对概念所反映的本质属性的挖掘过程。概念形成的过程是一个逐渐完善的过程，在这个过程中要准确把握概念的本质属性，教师就要“抓”住本质不放，然后充分地运用变式，不断地变换呈现形式，改变非本质属性，但本质属性不变，由此帮助学生准确理解概念。变式对于学生形成正确的概念有积极的促进作用，它有利于启发学生的思维，让学生透过现象看本质，使概念的本质属性更加突出，达到化难为易的效果。同时也有利于激发学生的学习兴趣，调动学生的学习积极性和主动性。

数学概念教学的过程就是数学模型形成的过程。因此学生概念模型的形成要經历掌握基本数学知识和技能，获得数学活动经验，感悟数学思想方法，形成良好的数学思维习惯和应用意识的过程。在这个过程中，教师要引导学生建立模型思想，从而提高学生解决问题的能力，发展学生的数学思维。

[ 参 考 文 献 ]

[1] 夏英美.如何引导小学生正确掌握数学概念[J].小学教学研究，2013（20）：21-23.

[2] 陈理荣.数学建模导论[M].北京：北京邮电大学出版社，1999.

[3] 刘仍轩.情境串教学法[M].青岛：青岛出版社，2005.

（责编 童 夏）