深度教学，让学习真正发生

许新新

[摘 要]深度教学是近些年教学研究倡导的一个热点。实施深度教学，数学教师要采取以下策略：从深度挖掘数学知识的文化背景着手，促进学生思维提升;从深度剖析数学问题产生、解决过程发力，促进学生思维生长;从深度解析数学认知建构方面主攻，设计充分有效的数学活动，让学生深刻感悟其中的思维策略;从解析数学知识运用方面引导，展现方法多样化，引导学生思维的灵活和创新。

[关键词]深度教学;深度解析;思维

[中图分类号] G623.5 [文献标识码] A [文章编号] 1007-9068（2021）35-0052-02

深度教學是近些年教学研究的一个热点。小学数学教师实施深度教学，必须着力深度解析知识来由、学习活动、策略运用和方法探究，以推动和引导学生深度学习。数学教师可以采取以下策略，引导学生深度掌握知识，并学会灵活运用和实现思维创新。

一、深度挖掘知识文化背景，促进学生思维提升

在教学数学新知识时，激发学生学习兴趣，使之具有探索和主动学习的欲望，是促进学生深度学习和提升思维的前提条件。教师可以深入挖掘数学知识的文化背景，以及相关的数学故事、数学史等数学文化，并相机穿插渗透，让学生兴趣满满，热情高涨。

比如，圆是教师和学生再熟悉不过的平面图形，然而他们未必都真正了解圆的相关背景知识。数学教学中如何渗透圆的文化，让学生认识圆的本质，促进学生思维的提升，是需要教师深入思考的问题。

最具人类文明标志性元素之一的“轮子”，抽象地看就是“圆”。生活实践中，人们发现轮子越大，转过一周的距离越长。于是人们开始深究：转动的距离与轮子的直径长短有什么关系？进而研究圆与直径的关系，以揭示“轮子也就是圆”的奥秘。

教学中，引导学生简要回顾人类研究圆的历程：从初步认识圆形物体到借助圆形物体得到一个圆;从用圆规画圆到计算圆的周长、面积等;从单独研究圆到研究圆与其他图形的组合;从以滚动实验初步体会圆周率的计算方法到圆的封闭、对称之美。在学习圆的过程中，圆周率是学生很感兴趣，也是印象最深刻的。对此，教师可以穿插渗透相关数学文化，如公元263年我国魏晋时期数学家刘徽由割圆术得到3.1416，称为“徽率”;1200年后，西方人才找到类似于刘徽的计算方法。到公元480年，我国南北朝时期数学家、天文学家祖冲之概括“割圆术”，得出圆周率在3.1415926与3.1415927之间，还用22/7和113/355这两个分数（称为“约率”和“密率”）作为圆周率的近似数值。这个记录保持了近千年。计算机的出现使圆周率的计算有了突飞猛进的发展，到二十一世纪六七十年代得到圆周率一百万个小数位数值。

深度解析圆的背景知识及其研究历程，以及不同时期圆周率的发现发展过程，能激发学生对数学文化的学习兴趣，让学生学会更全面、更完整地思考数学知识，从而促进学生深度学习。

二、深度剖析问题产生与解决过程，促进学生思维生长

美国当代数学家哈尔莫斯曾经说过：“问题是数学的心脏。”发现问题、提出问题、分析问题、解决问题贯穿在整个数学教学中。数学教师要引导学生深入探究问题的产生过程与解决方法，对问题前瞻、后顾，用问题引领学生深入学习，从而进一步促进学生思维生长。

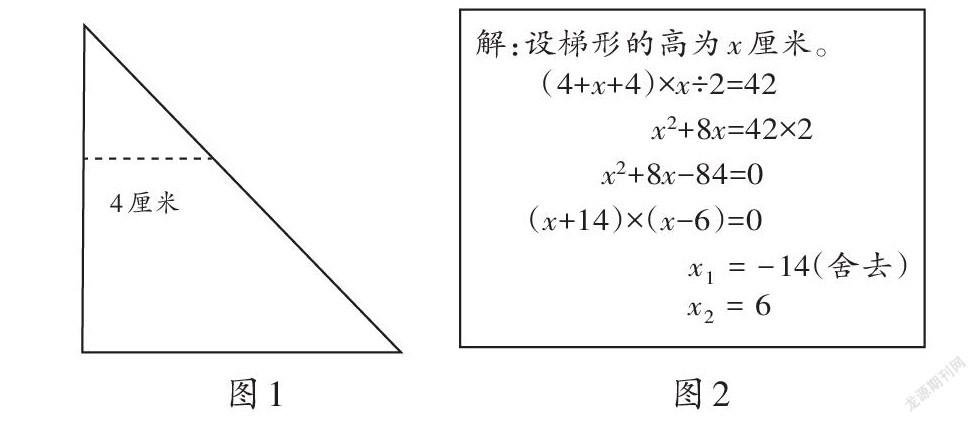
比如，著名特级教师王九红在一次教学中给学生出示思考题：将一个等腰直角三角形剪掉一个三角形后得到一个梯形（如图1）。已知梯形的面积是42平方厘米，上底长4厘米，梯形的高是（  ）厘米。

上例中剪掉的三角形是一个等腰直角三角形，根据梯形的面积公式可以列出如图2所示的方程，方程为一元二次方程，超出了五年级学生的接受范围，难度大。基于此，教师从问题出发进行针对性引导。

师：如果设梯形的底为x呢？

生1：（x+4）（x-4）÷2=42。

师：这个方程和之前的方程有什么区别？

生2：这个方程简洁、对称，容易解答。

师：你能把“÷2”移到右边再解答吗？

生3：可以。方程两边同时乘2，得到（x+4）（x-4）=42×2。

师：方程右边的“42×2”表示什么？

生4：42×2表示梯形面积42的两倍。

师：如图3，梯形的高也就是长方形的宽。那么，可用什么方法解（  ）×（  ）=84？

生5：可用一一列举法分解84的因数。

师：很好！请说具体些。

生5：84=1×84=2×42=3×28=4×21=6×14=7×12。经过验证得知长方形的宽是6厘米。

……

以上解答过程中，教师抛出问题“如果设梯形的底为x呢？”引发学生思考，学生列出另外一种方程，体会到解方程可以由直接设未知数变为间接设未知数，从而促进学生思维不断生长。

三、深度解析数学活动过程，感悟探究方法

数学活动不仅仅是动手实践，还包括各种数学运算、思维推理、解决实际问题等。在教学活动中，往往出现学生只知道呆板地算，不总结，不归纳，不思考，这是数学活动无法有效开展的表现。引导学生发现相应数学规律，完成算法归纳， 实现方法优化，是数学计算活动的重要任务。

例如，苏教版教材三年级上册第一单元“有趣的乘法计算”一课，在探索“同头尾合十”的两位数乘两位数计算规律时，教材首先呈现了三道竖式“22×28”“35×35”“56×54”，要求学生仔细观察、比较算式，并说说它们有什么共同特点，让学生在讨论和交流中逐步明确这些算式都是两位数乘两位数，且每个算式中的两个乘数：十位上的数是相同的——“同头”;个位上的数相加正好等于10——“尾合十”。在此基础上，要求学生算出每个算式的乘积，继续观察、比较得到的各个乘积，适当启发学生思考：所得的积的末两位各是多少？各是由哪两个数相乘得到的？积的末两位前面的数各是多少？它们又可看作哪两个数的乘积？由此，完成抽象概括：积的末两位是两个乘数个位上的数相乘的积，而末两位前面的数则是两个乘数十位上的数与比它大1的数相乘的积。这里的教学活动重点关注数据现象中隐含的特征，把握变化中不变的共性。让学生如此经历数学活动，有助于他们顺利总结，形成计算经验。

四、深度解析多样化思考路径，深层培养思维品质

郑毓信教授曾说：“数学深度教学的一个重要内涵，应当由突出强调具体的数学方法和策略，转变为注重一般性思维策略和思维品质的提升。”數学方法和策略是思维策略和品质提升的一个重要手段，教师应抓住本质，追求数学方法的灵活多样，以培养学生思维的灵活性，从而达到深度教学的目的。

例如，喝几瓶汽水问题：每3个空汽水瓶能换到一瓶汽水。现在买了10瓶汽水，一共能喝到多少瓶汽水？

方法一：操作演示。拿出10瓶汽水，实际操作演示，最终发现剩余2瓶汽水，需要借来1个空瓶（需还）凑足3瓶，喝完以后3个空瓶正好可换1瓶汽水，因此一共喝到15瓶汽水。

方法二：画图示意。

一共10瓶汽水，因为每3个空瓶换1瓶汽水，所以一开始能先换3瓶汽水，对应的这3个空瓶又换1瓶汽水，这1个空瓶加原来第10个空瓶再借1个空瓶可以换回1瓶汽水，还了借的空瓶后统计一共可以喝到15瓶汽水。

方法三：合情推理。3空=1瓶=1水+1空，3个空瓶可以换1瓶汽水，1瓶汽水就能喝到“1水”，剩“1空”，因此，2空=1水，也就是2个空瓶可以换1瓶汽水，一共有10瓶=10水+10空，10个空瓶可以换“5水”，所以10瓶=10水+5水=15水。买了10瓶汽水，可以喝到15瓶汽水。

方法四：推导计算。10× [1+12] =15，1瓶汽水喝掉算是“1水”，留下1个空瓶相当于“半（瓶）水”，一共10瓶汽水，也就是10瓶的[1+12]。

以上四种解题方法，每一种方法之间都有一根主线贯穿，即本题的本质：2个空瓶可以换1瓶汽水。如果思维深入这一层面，即可把问题顺利解决。引导学生多途径深度思考，深度解析题目本质，就能让学生找到多种解题方法，从而培养学生思维的灵活性，有效提升学生的思维品质。

综上，数学教学应超越具体知识和技能，深入到思维的层面，由具体的数学方法和解题策略过渡到一般性的思维策略与思维品质提升，从而有效培养学生的思维能力，促进学生深度学习。

[ 参 考 文 献 ]

[1] 中华人民共和国教育部.义务教育数学课程标准（2011年版）[M].北京：北京师范大学出版社，2012.

[2] 郑毓信.小学数学教师[M].上海：上海教育出版社，2019.

（责编 黄春香）