教学要“有方”,设计须“简约”
戚彤彤
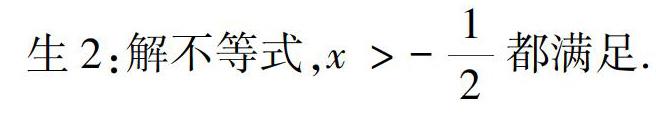
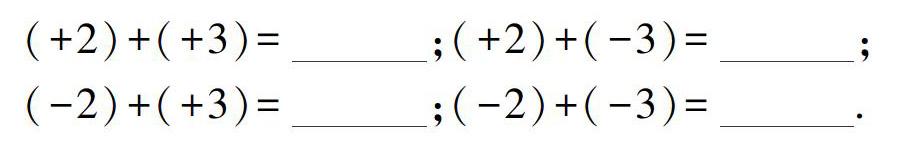

[摘要]简约教学,作为一种更具效度与深度的教学方式,正在被越来越多的数学教师所学习和采用。它不仅表现在形式上简洁与明了,更体现在教学方法、教学內容与思维训练上的深入浅出、通俗易懂。本文结合教学实例,从引入、例题和拓展三个角度,探讨简约教学如何实现有效性课堂,提升学生的数学核心素养。
[关键词]简约;教学;引入;例题;拓展
关注近几年初中数学的课堂变革。越来越多人在课堂形式和课堂设备上“别出心裁”。努力挣脱传统的教学模式。可是大多不尽人意,流于形式,迷失了数学教学本应有的效度和深度。在追求学生学习能力和数学核心素养的理念下。教师还是应回归到数学教学的本质上,思考如何更有效地开展教與学。简约教学,如一抹清泉如约而至。激发数学教师反思教学设计的简约有效性。
简约是数学教学的一种理性回归。正如徐长春老师在《简约教学艺术》中所讲:“简约教学并不是简单的压缩和简化,相反,它是一种深广的丰富,寓丰富于简单之中。凭借已有教学改革的成功经验。以先进的课程理念和教学思想为指导,对课堂教学进行反思、调整、提升,使课堂变得简洁、清晰、流畅、凝练、深刻,以实现课堂教学的审美化、艺术化、高效化的课堂教学境界”。基于此,笔者不揣浅陋,从引入、例题和拓展三个角度,欲就此以自己的教学实践,谈谈简约教学的一些做法。
1引入教学,简约而不简单
作为课堂的引入,往往有不成文的规定,即“简短”。过于花哨或冗长的引入往往会拖累课堂教学后续的完整性。导致头重脚轻的情况。因此,简约引入很重要,它对整节课的节奏起到关键作用。前知引入,对知识的回顾性很高。在常态课堂或展示课堂中常常作为首选。但容易出现“炒冷饭”的尴尬局面。如何将这种前知性引入发挥得更加简约有效呢?
1.对话式引入。短而精
复习课堂中常常面临的就是前知的重温。下面一个极其简短设计,以简约的对话形式,故设陷阱,引蛇出洞。让学生在认知冲突中究其根本。此案例的设计正因为以问答的方式展开。快速凝聚学生注意力。以微变式的判断由浅至深回顾知识要点。每个环节直击学生认知上的误区——明确不等式的定义。深化对不等式基本性质3的理解。
案例1浙教版数学八年级上册的《不等式复习》的3分钟引入。
师:请同学们判断黑板上2<1这个式子是不是不等式?
(众说纷纭)
生1:不是,2>1.
师:那我们回忆下什么叫不等式?
生(齐答):含有不等号的式子。
师:现在回看我们这个呢?
生:是不等式,只是不等式不成立。
师:对,那老师改动下,变成-2<1是否成立了?
生:是的。
师:如果再变成-2x<1,哪些x成立?
生1:x=0,1,2,…
师:解不等式要注意什么?
生:不等式两边同乘除负数,不等号改变。
师:这是我们本章不等式学习中最重要的一个性质!
2.放手式引入。单而厚
数学学习其实就是基于前知对未知的探索和验证的过程。在新课学习中。我们可以构建学生从旧知到新知的探索式引入,激发学生在“承前启后”的设计环节中。探索出新的数学规律。正如以下案例是一个有理数减法法则的“放手式”引入。
案例2浙教版数学七年级上册的《2.1有理数减法1》引入。
先设计了这样几个有理数加法的计算题进行热身训练,限时1分钟:
师:能在1分钟之内完成的同学。能否介绍下快速计算这几个加法式子的秘诀?
生1:有理数同号相加,符号不变,绝对值相加。
生2:有理数异号相加,符号取绝对值大的,绝对值相减。
师:同学们很好掌握了加法的诀窍。如果老师现在把加法都改成减法,同学们哪些式子会求呢?(学生开始动笔求解)
师:会解决第一个式子的同学有吗?
生1:-1
师:为什么你觉得是-1?
生1:2比3小1,不够减。所以是-1.
师:同学们觉得这位同学讲的有无道理?(生齐声同意)
生2:那我会求第二题,2比-3大,通过数轴可以发现2比-3大5,所以2-(-3)=5.
师:这位同学借助了刚学的工具(数轴),更加直观的为我们演示了两数差的运算。(师板演)(生掌声肯定)
师:那同学们其余的两个题,咱们能不能用这样的方法来求解下呢?
(生动手求解,师将学生的答案记录在黑板上)
师:为什么你认为是负的?
生4:不够减,所以结果应为负。
师:讲的非常好,但是我们如果按照这样的计算方式。我们好像会很慢,有没有像加法法则那样的秘诀呢?请同学们观察两列式子和结果,连线结果等价的式子。
师:减法运算能否转化为加法运算呢?如何转化?
生:减去一个数,等于加上这个数的相反数。所得的结果相等。
数的减法运算。本身来源于生活中量的比较。基于学生对数的大小比较和有理数加法法则的认知前提,笔者设计了开放式的有理数减法探究。学生可以通过已有的有理数加法认知和自身的探究学习力。基于生活经验下自然唤起了减法算理。抛弃了引导式教学。开放式的设计给学生更多的留白,促成了以生教生的效果。
2 例题教学,丰富于简单中
例题教学简约设计是为了更好的揭露问题本质。它需要精湛的设计,每一个细小的环节,都要深思熟虑。它看似平常,而平常中蕴涵智慧;它看似简单,而简单中孕育深刻。下面两个案例,小小的“留空”,激发出了思维的火花。从简洁的教学环节中给予的深刻教学意图。
案例3浙教版数学八年级上册的《不等式复习》。
(学生板演过程,师生共同批阅,并总结解不等式的步骤:去分母一去括号一移项,合并同类项一系数化1.所得结果x>-1.)
师:同学们,如果改变不等号右侧的数字,结果是否会影响?
(生均肯定)
生1:借助原来的过程,从结果开始,逐步进行倒推不等号右侧的数。
师:非常好。这位同学采用了我们数学中巧妙的倒推法。还有不同方法吗?
生2:我是正向法。将不等号右侧的数设为a,根據不等式的结果x>1.可得a的值。
师:同学们能理解这位同学的方法吗?这种就是我们数学中常用的待定系数法。对未知的设元。通过正向求解。对比结果,确定系数。
这个问题是在解不等式的基础上,仅是简单地“空”某一数字。却激发了学生对这个问题的深入思考,倒推法和设元待定系数法,两种方法就建立在学生对不等式解法熟练巩固。但这样的设计把无趣机械的解不等式。变为有技巧性的思维训练。既巩固了基本知识。又激发了学生深度思维。又如:
师:第一个方程很好解,而且两个解都是整数。(给出第二个问题)同学们还有没有数填入右侧后,使得方程有两个整数解呢?
生3:有很多。(其他同学很惊讶。)
师:哦?真的吗?你是怎么想的?
生3:我先假设x1和x2的整数解,然后返代回方程。
(此时其他学生恍然大悟)
师:那填人方程的数有没有最小的数,如果有,是什么数?如果没有,请说明理由。
生3:……
(学生都开始拼凑,但并未得到结果。老师开始引导学生,正向思考,若假定数a填人后有整数解,对方程的b2-4ac和韦达定理两根的和积进行分析。)
同样一个小小的“留白”。让学生可以从逆向和正向双向求解。能想到逆向的想法。其实是将不定的方程转化为代数式求值问题。而正向思考时,学生又需设元引参。对问题的整数解的分析需严谨又全面。“留空”的简约设计,给学生提供了更大的平台拓宽思路。
3 拓展教学,另辟思维“简”径
思维定势是人们长期形成的一种思维方向。它使人们以比较固定的思路和习惯考虑问题。当思维定势与问题解答途径不一致或不完全一致时。则思维定势就产生消极负面影响,使问题解答过程冗长繁琐,甚至会导致思路受阻,使问题解答半途而废。如何摆脱和克服思维定势所造成的负面影响?我认为在教学中。应该经常设计一些不按常规思维的例题。刺激学生的思维增长点,使之养成随机应变,寻找“简”径的习惯。
案例5求证不论a取什么实数。关于x的方程x2-(a2+a)x+a-2=0必有两个不相等的实根。
按常规解法,先计算判别式△,然后根据△的符号再得出结论。由于学生思路受“计算判别式△的思维定势”的影响。当求出△=a4+2a3+a2-4a+8时。发现它是一个关于a的四次多项式,学生顿时傻眼了。如何判断它的符号?解题陷入困境。倘若我们改变一下思维角度。将二次方程根的问题等价转化为抛物线y=x2-(a2+a)x+a-2与x轴的交点问题,马上就有“柳暗花明又一村”的感觉。要证明原命题成立。只需证明这个抛物线图象与x轴有两个不同的交点。由于它的图象开口向上,因此只要找到一个x的值使得y<0,那么问题就解决了。注意观察,不难发现当x=1时有y=12-(a2+a)+a-2=-a2-1<0.故y=x2-(a2+a)x+a-2图象与x轴有两个不同的交点。即原命题成立。
数学问题形式多样。千姿百态,解题者面对新题、活题。没有随机应变、因题制宜的能力是解决不了问题的。要提高思维的灵活性,在教学中,有时还要故设障碍,使学生在思维受阻时,能灵活运用基本知识和基本技能,打破常规,另辟“简”径,不失时机地克服思维定势的消极影响。这样思维能力就自然得到提高。
简约教学看似简单,学会简约却需要智慧的积累。在理解知识本质和教材设计意图基础上。用最简单的方式、简练的语言、简明的活动,实现学生对知识的深刻理解。所以,追求简约有效的数学教学,教师必须对手中教材进行深刻地思考钻研,要求对教材有独特而深刻的见解。深入研读教材,方能理解教材,取舍有度。但仅基于教材,没有厚度和深度的教学,那是简单,是不能促进学生发展的。因此。我们教师平时要有广泛地思维训练和积累,方能信手拈来,教学才会张弛有度。

