数学教学必须突出数学本质

李树臣 刘文成

[摘要]数学教学突出数学本质是提高学生数学核心素养的根本所在，数学核心素养的各项构成“指标”都是在突出数学本质的前提下。通过数学学习逐渐形成和发展而来的。数学教学中突出数学本质的宏观途径是精心创设问题情境，突出数学知识之间的內在联系，充分揭示数学概念（定理、法則、公式、规律）的內涵，引导学生经历数学知识的形成和应用过程。在过程中充分感悟有关的数学思想。

[关键词]数学本质;问题情境;数学概念;数学思想;经历过程

《义务教育数学课程标准（2011年版）》（以下简称《课标（2011年版）》指出“数学素养是现代社会每一个公民应该具备的基本素养”。数学教学的根本目的是为了提高学生的这种基本素养，实践证明，学生的数学素养是在反映数学本质的前提下，通过长期的数学学习逐渐形成和发展起来的。数学本质是指数学内容本身所固有的根本属性，是数学内容区别于其它学科内容的基本特质。数学教学如何反映数学的本质呢？这是大家都在思考与探索的问题，笔者认为应重点关注五个问题。

1精心创设问题情境

任何数学知识都不是“无中生有”的，都有其产生的基本“土壤”（也有应用的“场地”），在学习这样的知识时，教师首先要找到这样的“土壤”，并设计一些问题，然后用这样的问题引导学生进行探究、思考、交流等活动，在活动的过程中完成对知识的学习，这个过程就是创设问题情境。

创设问题情境对于学生的学习具有重要的作用，有的老师利用问题情境“澄清”对某些知识的模糊认识，从本质上把握数学知识。例如在学习等腰三角形的性质和判定时，由于学生搞不清楚二者之间的本质差别，经常出现把“等边对等角”与“等角对等边”混用的现象。为了帮助学生从根本上理解二者的本质。我们可创设下面的问题情境：

案例1小泽林的证明正确吗？

如图1，AC和BD相交于点O，AB//CD，OA=OB。

求证：OC=OD。

下面是小泽林给出的证明过程：

设计意图 这个案例选自学生学习过程中的真实案例，由于许多学生不能从根本上理解“等腰三角形的性质和判定”的本质，学习中往往不能正确选择利用，表现在解题时“混用”二者。本案例是为了帮助学生真正理解等腰三角形的“性质”和“判定”，明确二者的区别与联系：“性质”指的是已知这个三角形是等腰三角形，然后推出的一些结论，如等腰三角形的两边相等，两个底角相等。所以在等腰三角形的性质中“边相等”在前面，即“等边对等角”：而“判定”指的是根据一些条件来判断一个三角形是不是等腰三角形。“边相等”是推出的结论，应写在后面，即“等角对等边”。

教学中，利用学生容易混淆、模糊的知识点创设“矛盾”的问题情境是引导学生明确有关知识之间区别与联系的常用方法。这样的问题情境突出了数学的本质，符合《课标（2011年版）》提出的“帮助学生理清相关知识之间的区别和联系”的要求。

2 要注重突出知识之间的内在关联

“数与代数”“图形与几何”“统计与概率”三部分之间的内容以及每个部分内部的知识之间都存在着“实质性”的联系，教学时，突出有关数学知识内容之间的关联，就能揭示出教学内容的数学本质，有助于学生理解数学的本质。

案例2平方差公式的探究发现过程。

平方差公式（a+b）·（a+b）=a²-b²，是整式乘除中的一个重要内容。把公式的左、右两边交换位置得到a²-b²=（a+b）（a-b），利用这个公式可以进行因式分解。为了引导学生自己探究发现公式a²-b²=（a+b）（a-b），我们从“数形”之间的联系出发，引导学生探索如下：

实验操作

（1）剪一个边长为a的正方形硬纸片;

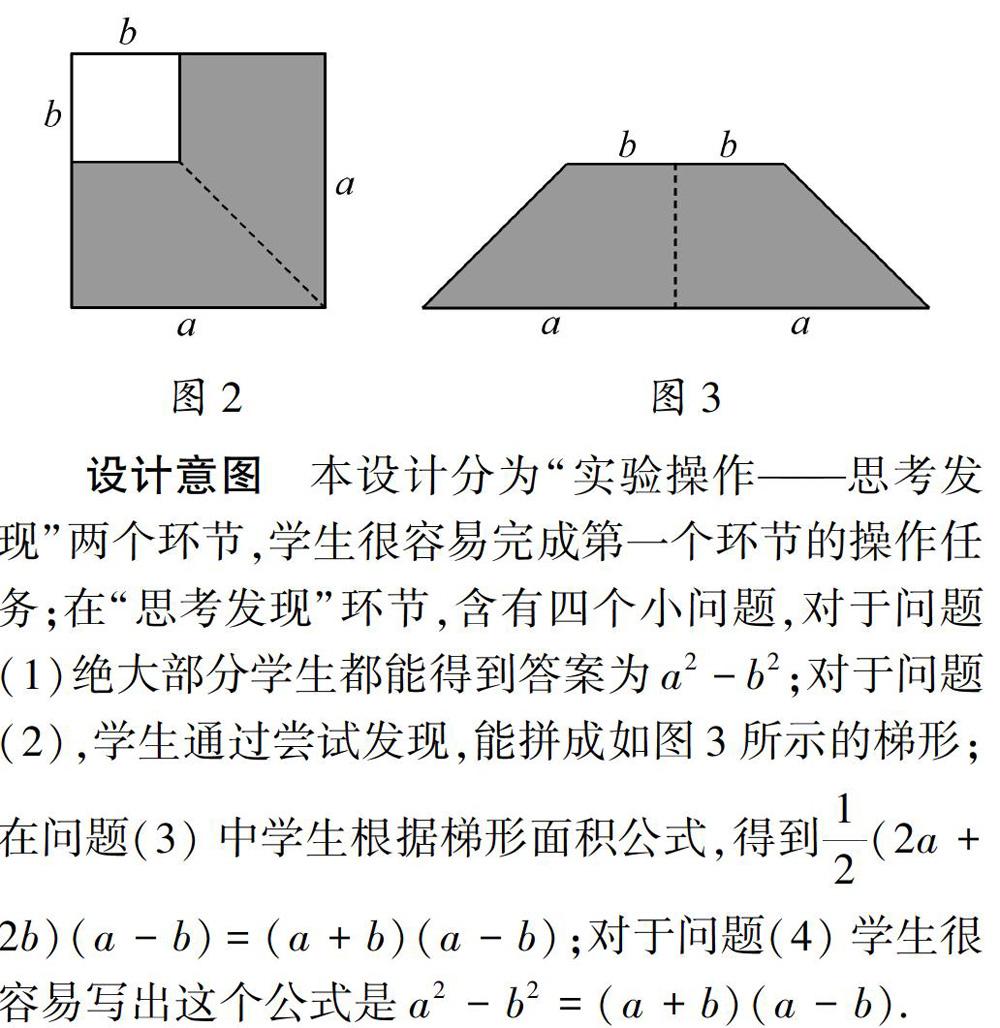
（2）按照图2所示的方式，在边长为a的正方形硬纸片上，剪去一个边长为b的小正方形（a>b）：

思考发现

（1）图2中减去边长为b的小正方形后，剩下部分（阴影部分）的面积为____;

（2）如果把剩下的部分（阴影部分）沿着虚线剪开，然后利用这两部分纸片进行拼图试验，那么你能拼成一个怎样的图形？相互交流。

（3）计算你拼出的图形的面积____;

（4）由此你能得到一个怎样的公式？请写出来：____。

学生在上述问题的引导下，从“几何”的角度得到了“代数”的结论，更加认识到代数与图形之间存在的固有联系，并且加深了对数形结合思想的认识和理解。积累了数学活动经验，在以后的学习过程中，当他们再遇到类似的情境时，便能积极主动的开展数学探究活动，这样的活动可以培养学生运用数学思想和方法观察问题、发现问题、提出问题和解决问题的能力。

教学中，教师要把每堂课的知识置于整体知识的体系之中。引导学生通过学习逐步体会到知识的结构和体系，从而感受到数学的整体性。

3 充分揭示数学概念的内涵

数学概念的内涵反映了数学的本质，对于数学概念的教学一定要充分揭示其内涵。数学概念的建立过程大致需要经过“感知-分析-概括-表述”四个阶段，首先教师要创设问题情境，给出一些问题，引导学生在对问题进行思考的基础上形成感性认识，然后教师给出若干个具有这种“特性”的“结构式子”，让学生进行观察与分析，由此抽象概括出它们的本质，最后给出规范的数学定义。为突出数学概念的本质属性，应从這个概念的内涵与外延上进行深层次的剖析。

案例3正弦概念本质的分析过程。

《课标（2011年版）》指出“利用相似的直角三角形，探索并认识锐角三角函数（sinA，cosA，tanA）”。笔者认为在这些概念的建立过程中“相似三角形的对应边成比例”中的“比”是核心知识。把锐角A的正弦、余弦、正切叫锐角三角比更能反映它们的实质。

锐角三角比在本质上是个“比”值，为突出这个比值，可设计下面的问题情境：

操作计算

（1）如图4，把平放在地面上的长为2m的平滑木板AB的一端B抬高1m。在木板上分别取点B₁，B₂，B₃，B₄，并量取它们到A点的距离AB₁，AB₂，AB₃，AB₄，以及它们距地面的高度B₁C₁，B₂C₂，B₃C₃，B₄C₄，数据如下表所示：

剖析本质

以正弦为例结合图5与图6，通过相互讨论、交流、归纳出正弦的本质。

①正弦在本质上是一个“比”：

④因为|y|≤r，所以这个比值不会超过1.

如图6，只要点P（x，y）确定了，三个量x，y，r也是确定的，任意两个量都能确定一个比值，由此可得六个比值。因此，基本锐角三角比有且只有六个，这便是锐角三角比的外延，我们在初中仅学习其中的三个。

研究表明，一个新的概念如果没有操作过程很难转变成一个数学实体。因此，在对数学概念、原理（定理、法则、公式、规律）的教学中，首先要认真研读教材，分析概念、原理的本质，然后设置一个问题系列，以此引导学生通过对问题的思考、探索，找出概念、原理的内涵，在此基础上给出概念和原理。只有这样学生才能从“数学本质”的高度上去理解数学概念数学原理的实质。

4 突出数学思想

日本数学教育家米山国藏曾经指出：学生在校学过的数学知识一段时间不用，很快就会忘掉，但是数学的精神、思维方法、研究方法和着眼点却随时随地发挥作用，相伴终生。数学思想同数学概念、定理、法则、规律以及描述它们的数学语言一样，都是数学的基础知识，这种知识“蕴涵在知识形成、发展和应用的过程中，是数学知识和方法在更高层次上的抽象与概括”，突出数学思想的教学，能注重知识之间的联系，当然也就突出了数学的本质。

案例4感悟模型思想的“載体”分析。

《课标（2011年版）》在“总目标”中提出的“基本思想”主要包含三种，模型思想是其中的一种，模型思想主要是在建立数学模型的过程中形成和发展起来的。数学模型就是根据特定的研究目的。采用形式化的数学语言，去抽象地、概括地表征所研究对象的主要特征、关系所形成的一种数学结构，“模型思想的建立是学生体会和理解数学与外部世界联系的基本途径。”数学与外部世界的联系体现在“数学化”上。数学化的本质就是“数学模型”的运用。

模型思想是学生在建立数学模型的过程中，逐渐感悟形成的，在“数与代数”“图形与几何”“统计与概率”的内容中存在着大量的“数学模型”，例如，用字母、数字或其他数学符号构建得到的代数式、关系式、方程、函数、不等式，以及各种图表、图形等都是数学模型。近几年中考题中涉及的主要数学模型有：方程（组）模型、不等式（组）模型、函数模型、几何模型（或三角模型）、统计模型、概率模型等。利用这些模型可以解决的问题涉及学习、生产和生活的方方面面。

让学生感悟模型思想的知识“载体”散见于《课标（2011年版）》界定的课程内容之中，建立“五光十色”的数学模型解答“丰富多彩”的数学问题是帮助学生感悟、形成模型思想的重要途径。对于“模型思想应该在数学本质意义上给学生以感悟，以形成正确的数学态度。”学生在学习这些“载体”知识时，教师要及时设置一些通过建立相应“模型”解决的实际问题，引导学生去解答。这样学生就不仅能学好这些知识，还能感悟到模型思想。并且能实现“体会数学知识之间、数学与其他学科之间、数学与生活之间的联系的目标。

数学思想是以具体知识为“载体”的，是数学知识的“灵魂”，教材就是用数学思想“串联”起来的，要突出数学本质，就必须让学生在过程中感悟数学思想，而且感悟的过程还要体现“逐级递进、螺旋上升”原则。

5 充分展示知识的形成和应用过程

华罗庚先生曾说过：“不要只给学生看做好了的饭，更要让学生看做饭的过程，数学教学要设法使数学知识‘活起来。”注重过程教学是体现数学本质的使然。这里的过程主要指：

5.1 知识的形成过程

在引导学生探究、学习一些新的数学知识时，教师要按照“知识背景一知识形成一揭示联系”的程序进行。设置一些引导学生进行数学活动的问题系列，让他们以“再发现”和“再创造”的方式经历一些数学过程。这样的导学过程能激发学生的学习兴趣，更好的理解数学的实质，了解知识之间的关联。如前面的案例2就很好的体现了平方差公式的探究发现过程。

5.2 知识的应用过程

在学生掌握了具体的数学知识后。教师要按照“问题情境一建立模型一求解验证”的程序设置一些运用这些知识解决问题的活动。学生在解决问题的过程中，特别是在解决一些综合程度稍微高一点的问题时，不仅能加深对有关知识的理解，明确知识之间的相互联系，还有助于学生整体把握数学知识结构，更好的认识数学的本质。

知识的应用过程分为“单一”知识的应用和多个知识的“综合”应用。前者主要体现在日常的数学学习过程之中，当学生每学习了一个具体知识后，就及时设计能利用这个知识解决的问题。例如。在学习了各种具体方程的解法后，都可以设计通过列这种方程能解决的具体问题，通过解答这样的问题，能让学生反复体会到“方程是刻画现实世界数量关系的有效模型”。对于方程的本质也就有了进一步的理解。后者则体现在“单元”复习或“综合复习”之中，解答这样的问题往往需要综合运用多个知识点才能解决。

（1）当v=2时，解答：

①求S_头与t的函数关系式（不写t的取值范围）;

②当甲赶到排头位置时，求S_斗的值;在甲从排头返回到排尾过程中，设甲与位置O的距离为5fI，（m），求S_甲，与t的函数关系式（不写t的取值范围）。

（2）设甲这次往返队伍的总时间为T（s），求T与v的函数关系式（不写v的取值范围），并写出队伍在此过程中行进的路程。

析解：（1）①排头与O的距离为S_斗=队伍的速度×行进时间+队伍的长度，排头走的路程为2t，则S_头=2t+300;

②当甲赶到排头时，有4t=2t+300，得到t=150，此时，S_斗=2×150+300：600（m）。

甲从排头返回到排尾用的时间为t-150.则S_甲=600-4（t-150）=-4t+1200.

设计意图 本题是基本的“行程问题”，本质上是由追及与相遇问题“合成”的问题。将其“还原”为“甲在初始地，排头在距甲300米处。两者同时开始向前进。甲的速度为2v，排头的速度为v，一段时间后两者相遇：相遇后排头继续前进，甲反向前进，两者速度大小不变，当排头与甲相距300米时，两者同时停下”。

本题主要考查学生综合利用方程、一次函数、反比例函数解决实际问题的能力，解答的关键是将甲与队伍分开来分析，把行程问题分为两个小问题分别进行思考。学生通过解答本题，不仅进一步加深了对方程、一次函数以及反比例函数的理解，而且更加体会到这些知识本身存在的内部联系，从而加深对数学本质的认识与理解。

数学教学必须突出数学的本质。以上讨论了数学教学中突出数学本质的五个宏观途径。为实现提高学生数学核心素养的教育目标，教师应认真研究《课标（2011年版）》，结合学习内容，精心设计问题情境，在引导学生经历各种活动的过程中，实现掌握知识、把握概念本质、感悟数学思想、体验知识之间的相互联系，这都是突出数学本质的具体表现。