“概念变式教学”提升核心素养

陈丽真

[摘  要] 数学概念是数学学习的核心与基础，准确理解数学概念是学好数学的前提，数学概念的学习要领会数学抽象的过程，概念变式教学旨在从不同角度深刻辨析概念的内涵与外延，提升学生的数学抽象等核心素养.

[关键词] 数学概念;变式教学;数学抽象;数学运算

概念是事物本质的反映，是对一类事物概括的表征. 数学概念是数学的根基，概念教学是课堂的重要环节之一，是数学教学的核心和基石. 那么，如何让学生深刻理解、准确掌握数学概念？概念变式教学旨在从不同角度深刻辨析概念的内涵与外延，提升学生的数学抽象素养，提高课堂教学效率. 在概念教学中，通过图形变式、语言变式、符号变式等探究活动，使学生对概念获得多角度的理解，对概念的本质有更深刻的认识.

[?]利用变式，抽象概念直观化

例1：设A，B是非空的数集，如果按照某种确定的对应关系f，使对于集合A 中的任意一个数x，在集合B中都有唯一确定的数f（x）和它对应，那么就称f：A→B为从集合A到集合B的一个函数，记作：y=f（x），x∈A. 其中，x叫做自变量，x的取值范围A叫做函数的定义域;与x的值相对应的y值叫做函数值，函数值的集合叫做函数的值域. 显然，值域是集合B的子集.

“函数”是高中数学的一个重要概念，用集合与对应的语言刻画函数概念比较抽象，学生理解困难. 为了帮助学生准确理解这个抽象的数学概念，可以让学生讨论并尝试完成下列问题，老师再逐一讲解.

分析：函数是特殊的映射，函数定义中强调“三性”：任意性、存在性、唯一性，這三性只要有一个不满足，便不能构成函数. （1）集合A不是数集，明确了函数的特殊所在;（2）集合A的元素0在B中没有与之对应的元素，不满足“任意性”;（3）集合A的元素1在B中有两个元素1，-1与之对应，不满足“唯一性”;（5）集合A的元素3在B中没有与之对应的元素，不满足“存在性”. 只有（4）和（6）满足函数的概念，而（6）集合B并不是该函数的值域，体现了“值域是集合B的子集”.

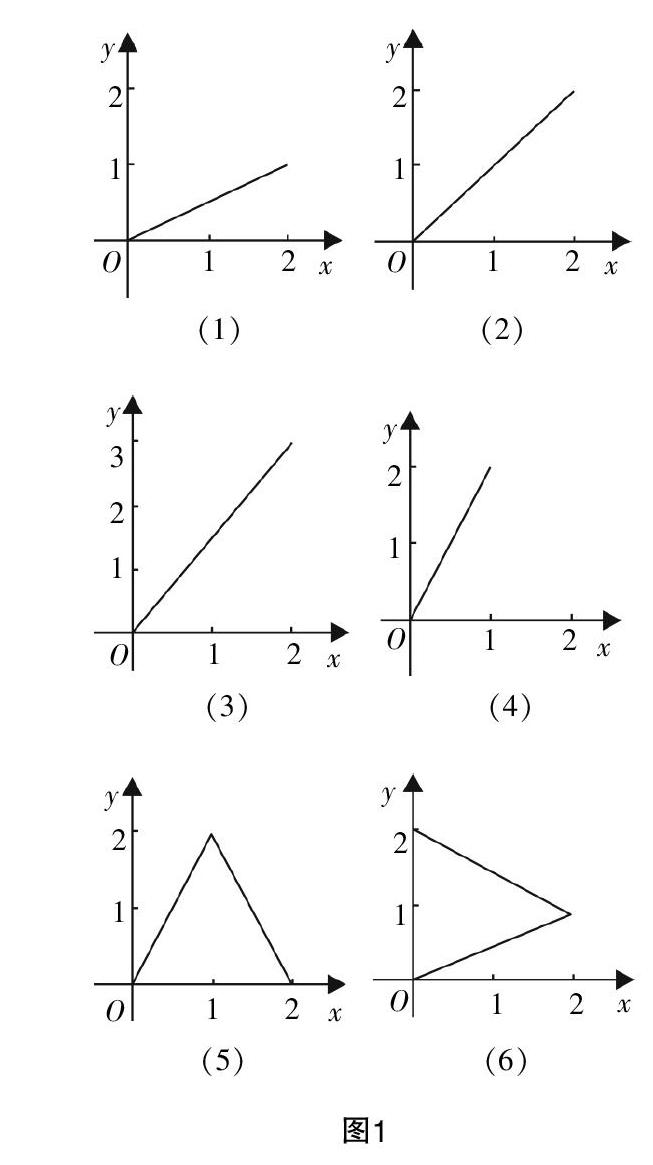
分析：图像是函数的一种重要表示形式，定义域、值域和对应关系是决定函数的三要素. 在函数概念中提到“x的取值范围A叫做函数的定义域”，“值域是集合B的子集”. 学生要会借助“三要素”，分析、判断图形是否为函数的图像. （3）中值域是[0，3]，不是集合B的子集;（4）中定义域是 [0，1]，不是A;（6）中0≤x<2时任意的x有两个y值与之对应. 所以只有（1）（2）（5）符合题设函数的概念.

数学概念非常精炼，寓意深刻，要仔细推敲概念中的每一字、每一词，理解准确到位. 以上变式从“数”到“形”着力体现“函数”这一概念中的关键字眼：“数集”、“任意”、“存在”、“唯一”. 通过直观、具体的变式，建立感性经验和抽象概念之间的联系，用不同的变式揭示概念的本质，通过对本质特征的分析，加深对整个概念的理解. 教学中，设置反例、错例辨析的变式训练，通过对问题正面、侧面、反面的分析，帮助学生理解概念的本质，并能运用概念发现问题的症结所在，达到去伪存真、由此及彼的目的.

[?]利用变式，拓展概念的内涵及外延

变式教学要源于课本又要高于课本，做到遵循课标，突出重点. 本例对“函数单调性”的概念从条件的等价性（变式1、2），结论与条件的转换（变式3、4），否命题（变式5）与逆否命题（变式6）等进行不同角度、不同层次的变式，有意识地引导学生发现变化中的不变，学生不仅获得对“函数单调性”这一概念的等价形式，又为函数单调性的应用，如利用单调性比大小、解抽象不等式的学习打下基础. 如此，对概念的建构提供一个有层次的推进过程，让学生多角度地理解概念，对学生掌握知识、促进思维和培养能力等方面起着非常重要的作用.

[?]利用变式，辨析易混淆的不同概念

在人教版《数学选修2-3》的第二章《概率》中介绍了两种离散型随机变量的概率分布：超几何分布与二项分布.课标要求学生能通过具体实例，认识这两种概率模型，并能运用这两种模型解决一些实际问题，但不少学生没有掌握好这两种模型，不能准确地辨别所要解决的问题是属于超几何分布还是二项分布，常混淆应用.

教师应引导学生认真审题，通过例题与变式用词的不同，正确辨析两种不同的分布. 从抽取的方式上，超几何分布是无放回的，二项分布是有放回的;从独立性上，超几何分布是不独立的，二项分布是相互独立的;当产品的总数很大而被抽出的产品较少时，超几何分布可以当作二项分布. 一般地，若以样本数据估计总体情况，或以样本频率代替总体概率，则是二项分布问题.

数学核心素养是在学生与问题的有效互动中得到提升的. 本例通过变式，创设不同的问题情境，使学生在具体问题的体验中辨析不同的概念，并通过对材料的分析，抓住问题的数学本质，培养学生数据分析与数学运算的素养.

例4中a，b可能取值都是四个，基本事件是有限的，变式中a，b可取[0，3]上的任意实数，基本事件是无限的. 这样，学生更清楚区别“古典概型”和“几何概型”的关键在于：古典概型的基本事件是有限的，几何概型的基本事件是无限的. 并且，两道变式又教会学生如何区分是“与长度有关的几何概型”还是“与面积有关的几何概型”. 因此，在教学中教师应针对相似概念的易混淆点，恰当巧妙地设计一些变式，帮助学生更好地理解、区分不同的概念. 唯有这样，学生才能正确运用概念解题.

高中数学教学应将数学核心素养的培养贯穿于教学活动的全过程，要有意识地将发展学生数学核心素养作为教学的导向，数学概念的教学是发展学生核心素养的重要载体. 通过教学实践发现，在概念教学中恰当地设置变式问题，可以有效地呈现概念的本质属性、清晰概念的内涵及外延，能让学生多方面、多角度地加深对概念的理解，拓展知识;设置层层递进的变式问题，引导学生从不同的角度分析、用不同的方法解决，能提高学生分析问题的能力和迁移能力，培养学生的数学思维品质. 这对教学内容及发展学生的个体能力，都能产生积极的促进作用. 然而，变式教学不能变成教师整节课的精彩演绎和拓展，不能教师讲得神采飞扬，学生听得应接不暇.教师必需注意学生的认知水平，结合具体的教学内容创设适合的变式，控制变式的数量及变式的深度，发挥概念变式的积极教学意义，提升学生的数学核心素养.