中学生对“字母表示数”认知发展的历史相似性研究

陈静安，黄启亮，凡加云，邬鸿钦

(1.广东第二师范学院 数学系， 广东 广州 510303；2.六盘水第七中学， 贵州 六盘水 555300)



中学生对“字母表示数”认知发展的历史相似性研究

陈静安1，黄启亮1，凡加云2，邬鸿钦1

(1.广东第二师范学院 数学系， 广东 广州 510303；2.六盘水第七中学， 贵州 六盘水 555300)

摘要:“用字母表示数”是中学数学的重要内容，同时也是中学生从文字代数向符号代数过渡的重要阶段.运用测试卷对七年级和高一年级学生关于“用字母表示数”的理解进行抽样测试的结果显示，学生对“用字母表示数”的认知发展过程与“字母表示数”意义演进的历史发展过程存在显著的相似性.这种历史相似性对“用字母表示数”相关内容的教学与教材的编写都有着重要的启示意义.

关键词:用字母表示数；文字代数；简写代数；符号代数；历史相似性

1问题背景

在数学发展的历史长河中，从算数到代数飞跃的标志是数学符号的引进.符号的引进，是数学准确并简捷地表达概念、命题、证明及方法的必由之路[1]75.没有符号的数学犹如没有文字的语言一样难以传承、发展和不可思议.特别地，“用字母表示数”不仅是人类由自然的“算术语言”向抽象的“代数语言”过渡的开始，也是学生代数学习的入门知识以及后续学习方程式、不等式、函数等知识的重要基础.为此，《义务教育数学课程标准》在各学段中都将“数与代数”作为数学课程的重要组成部分，并且在第二学段目标明确要求“在具体的情景中能用字母表示数；了解等量关系，并能用字母表示”，在第三学段目标强调“借助现实情景了解代数式，进一步理解用字母表示数的意义.能分析具体问题中的简单数量关系，并用代数式表示.”[2]

但是，教学实践中，对“用字母表示数”的认知、理解和运用是学生代数学习中的难题和高门坎，因此成为课堂教学的难点.如蒲淑萍和汪晓勤研究了上海市七年级学生对字母的认知水平，结果显示学生对字母意义的认知水平大多停留在“记数符号”和“未知量”的层次，对于字母表示“一类量”的思想存在认知困难[3]；虞琳娜针对小学生在自然数的表示中感悟字母的含义的研究发现，学生对“用字母表示数”的理解停留在“理解用字母表示一个数，但是难以想象这里字母表示的数可以是任意的”[4]；薛文叙关于学生对数和数的表示形式认知情况的案例研究发现，学生关于“用字母表示数”的理解存在诸多问题和障碍，例如学习了字母表示数后，对字母表示一类量并不理解、依然依赖于文字叙述的方式解题[5].受斯宾塞、波利亚等人关于“个体知识发生过程遵循人类知识的发生过程”的历史发生原理，以及克莱因“生物发生学的一项基本定律指出,个体的成长要经历种族成长的所有阶段,顺序相同,只是所经历的时间缩短……我想教授数学和其他任何事情一样,至少在原则上要遵照这项定律”的启发，本研究选取中学学段七年级和高一年级两个具有典型代表性的年级作为样本进行测试分析，并比对“用字母代表数”的历史演进过程，旨在了解七年级和高一年级学生对“用字母表示数”的认识、理解和运用与历史发展的相似性，以期对用字母表示数相关内容的教学提供一些有益的启示.

2研究过程与方法

为检验历史相似性，首先采用文献分析法，以厘清“用字母代表数”的历史发展和已有研究对学生“用字母代表数”理解存在的困难分析.其次，为检验历史相似性，运用问卷测试法和随机抽样对云南省某中学七年级30人和高一年级28人进行调查测试.问卷选取文[3]设置的3道测试题，测试卷紧扣《义务教育数学课程标准》对“用字母表示数”的目标要求:“在具体的情景中能用字母表示数；了解等量关系，并能用字母表示”，围绕“用字母表示数”的意义理解及其对应的3个历史发展阶段，旨在了解学生对用字母表示数的理解和运用水平，由此分析学生对字母表示数的认知发展过程与该知识发展的历史是否存在相似性.具体测试题目如下： 试题1：游乐场的大转盘的最高点、最低点分别距离地面110m、10m，这个大转盘的半径是多少？

试题2：已知圆的周长为r，圆的面积是多少？

试题3：已知两个数的和与这两个数的差，求这两个数？

3字母表示数的历史演进过程

追溯历史，不难发现，“用字母表示数”作为代数学最基础的内容，是四大文明古国和希腊人、阿拉伯人、西欧人接力完成的伟大成就，其间主要经历了古老的文字表达算术、丢番图用字母表示未知数、直至韦达与笛卡尔系统的符号表达3个质变、关键时期.19世纪德国数学史家内塞尔曼依据时间顺序并结合代数的表达方式在其《希腊代数》中首次将代数学的历史演进过程划分为3个主要阶段：文字代数、缩写代数、符号代数(或者修辞代数→缩略代数→符号代数)[1]75.

3.1文字代数阶段

公元3世纪以前、即古希腊丢番图以前的时期，无论是河谷文明著称的四大文明古国、还是海洋文明的领军者古希腊，人们都还没有想到使用任何符号表示数，所有数学问题及讨论解决都是用文字来表达和说明[6]65.如我国用天、地、人、物表示未知数，甲、乙、丙、丁表示已知数而命名的天元术、四元术等代数.总之数学停留在用文字作为记数符号阶段，故这一时期的代数史称文字代数或文词代数、修辞代数.

3.2简写代数阶段

公元3世纪到15世纪的代数以引入字母代表未知量为典型特征，其中公元250年左右的数学家丢番图被称为古希腊代数学的鼻祖，是这一时期的典型代表.他在其《算术》中首次创用了一套缩写符号，特别是他使用特殊的符号ζ表示未知数并用于计算，使得后人相信，尽管他的思想受到前期古希腊的深刻影响，但是他已经完全摆脱古典时期的束缚.此外，他还创用↑表示减号，用专门的符号表达乘幂等[6]65.之后尽管越来越多的数学家使用不同的字母表示不同的量，但是可以看出字母总是表示未知量，而没有一帆风顺地朝着代表“一般量”、“一类量”继续发展.这一时期是真正的符号代数出现之前的一个重要阶段，数学史上称为简写代数或缩写代数、缩略代数阶段.

3.3符号代数阶段

16世纪法国杰出的数学家韦达在其1591年的著作《分析引论》中第一次有意识地系统引进字母来表示未知量、系数和方幂，体现了他对符号系统深刻的认识.他采用辅音字母表示已知量，元音字母表示未知量.同时规定算术与代数的分界，他认为算术运算是施行于具体的数，而代数运算则施行于事物的类或者形式，因此把符号代数称作“类的算术”以区别旧的“数的算术”，使代数学成为研究一般类型的形式和方程的学问，因其抽象而应用更为广泛[6]129，为算术到代数的飞跃作出了卓越的贡献.值得一提的是，17世纪的笛卡尔进一步对韦达使用的字母作了改进，创造性地用拉丁字母前面的字母a,b,c,d,…等表示已知数，用后面的字母x,y,z,w,…等表示未知数，使字母表示得到了统一[7]，并且一目了然、系统全面，基本形成了现今的习惯用法.至此，代数学进入了符号代数、又称字母代数的时代.

总之，人类对“用字母表示数”及其意义的认知呈循环往复、螺旋上升的过程，并经历了“表示特定的数→表示未知量→表示一类量”的历史演进过程，代数学历经3个阶段、3 000多年缓慢曲折和艰辛的发展，最终得以演进成今天成熟、完善的符号代数体系.

4问卷测试结果与分析

4.1问题1的测试结果及分析

测试结果包括如下3类：

(i)没有使用字母的文字解法：此圆半径为(110-10)/2=50m.七年级和高一年级学生对应的解题方法和过程：(110-10)÷2=100÷2=50(m),答:半径是50m.

(ii) 使用字母表示半径的简写代数解法：R=(110-10)/2=50m.七年级和高一年级学生对应的解法:

(iii)没有或者不能解决问题(换言之，学生的解法中缺失用字母表示未知数、解一元一次方程的符号代数方法).

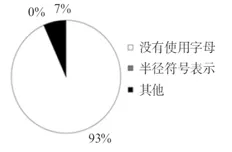
图1七年级使用字母情况统计

结果分析：七年级和高一年级在问题1解法中使用字母的统计结果如图1和图2所示.其中，采用算术解法(i)、即没有使用字母的七年级学生有28人，占被试的93.3%；高一年级有7人，占比25%.这表明刚从小学升入初中的七年级学生总体还停留在代数初始阶段的文字代数即小学算术思维水平，而高一年级学生虽然在课堂教学上已经进入符号代数阶段，依然有两成多的学生习惯于文字代数思维，尚未养成用字母表示数的意识和习惯，没能够与时俱进上升到简写代数与符号代数认知水平.

采用R表示半径的简写代数解法(ii)，七年级学生人数为0，高一年级学生有20人、占被试的71.4%；但高中生被试中依然没人采用字母表示未知量的方程解法.这说明七年级学生虽然已经接触简写代数方法，但是他们习惯于或更擅长用算术方法分析和解决问题；高一年级相对七年级学生学习和运用简写代数与符号代数的时间较久，七成进入了简写代数水平，但仍然没有学生用字母表示未知量，总体仍停留在较低层次的“记数符号”认知水平.此外，有初中生被试2人和高中生被试1人没有或者不能解决问题(iii).综上，或许说明相对于用字母表示特定的数，用字母表示未知量除了解题策略不同，还因为涉及对字母表示数的意义的认知水平、思维和表达习惯等多个层面的质变，无论对于初中生或者高中生都更为困难，而成为认知和教学的难点与高门槛.

这启示我们：一方面，简写代数与符号代数思想的获得不是一帆风顺、一蹴而就的，学生需要相对较长的时间来理解和接受；另一方面，高一年级被试随着年级递进、浸泡在字母代数里的时间增加，“用字母表示数”的意识与能力相比七年级学生得以增强.这从两个方面映射出学生对于“用字母表示数”意义的认知演进过程与简写代数到符号代数历经3 000年漫长的历史发展过程存在明显的相似性.

4.2问题2的测试结果及分析

测试结果包括如下3类：

(i) 把字母r视为半径和已知量求得面积的错误算法：这个圆的面积是πr2.

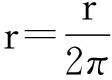
(iii)其他，即没有或者不能解决问题.

结果分析：问题2解法中七年级和高一年级学生对字母r的理解的统计结果如图3和图4所示.其中，采用错误解法(i),即把r视为半径并看做已知量的学生，七年级被试有6人，占20%；高一年级有3人，占了10.7%.甚至有些学生以为题目出错了，把题目中的周长改为半径.究其原因，这或许受制于被试在小学通常用字母r表示圆的半径的影响，一味地、机械认为r只能表示半径，对字母r可以表示任意未知量还存在困难，没有达到字母可以“表示一类量”的认知水平，因此这部分学生对字母意义的理解与运用还停留在简写代数的记数水平.

采用解法(ii),即把r看作已知量周长，并得到正确结果的七年级学生有16人，占53.3%；高一年级有21人，占70%.值得注意的是，在大多数学生采用的解法(ii)中，r既表示已知量周长、同时又表示未知量半径，这或许说明这部分七年级和高一学生对用字母表示数中的已知量和未知量都有一定的认知，但同时受小学一个字母常常表示一个特定的数的影响，对于字母作为“记数符号→表示未知量→表示一类量”3个层级意义的区别与联系的认知还不够明确与清晰，以致在具体的情景中涉及用字母表示数去解决问题时，往往容易陷入模糊不清和混乱胶着状态.

图2高一年级使用字母情况统计

测试结果(iii),即没有或者不能解答此题的被试比例如图3和图4中的其他所示.排除学生粗心等原因，并结合测试结果(i)中“将字母r当作半径的理解, 甚至有些学生以为题目出错了，把题目中的周长改为半径”的做法，这一方面折射出学生心目中r这个字母的特定意义对认知和理解具体问题(这里表现为本测试题)中字母r的意义形成负面干扰，导致被试不知所措、无从下手；同时也反映了这部分学生对字母表示数的认知水平停留在“一个字母只能代表一个确定的量”的认知水平.这与历史上曾经只用某个字母表示一个特定的量不谋而合、具有相似性.

总之，七年级有近五成、高一年级有三成的被试对于字母r可以表示任意一类量的认知存在困难，没有达到字母可以表示一类量的认知水平；高一年级相对七年级学生，把r看作已知量周长并得到正确结果的学生数提高了近20个点.这清楚地表明，学生随着学习经验的丰富、年级的递增，对字母表示数的认知与运用得到了提升和发展，整体上符合人类对“用字母表示数”意义的认知呈循环反复、螺旋状缓慢上升的过程.

4.3问题3的测试结果及分析

测试结果包括如下3类：

(i) 文字代数解法：文字表达.

七年级和高一年级对应的文字代数解法：把这两个数的和和差加起来，设其中一个数为x，另一个数为y，那么x+y和x-y加起来可以写成x+y+x-y，化简为2x,2x就等于这两个数的和加差，把这个方程化简出来就得到了x,再用这两个数的和减去x的值就等于y.(注：题目中已知两个数的和与差)

(ii)简写代数的解法，以丢番图的解法为例：设两数之和为m，两数之差为n，设较小数为x，则较大数为x+n，据题设有2x+n=m，所以较小数为(m-n)/2，较大数为(m+n)/2.

学生对应的解法：

甲-乙=19,甲+乙=29，

设乙为x；当甲-乙=19时，则甲=乙+19.又甲+乙=29.即(乙+19)+乙=29,(x+19)+x=29,2x=29-19,2x=10,x=5.所以甲=乙+19=5+19=24.答:乙为5，甲为24.

(iii)符号代数的解法，以韦达的解法为例：设两数之和为a，两数之差为b，其中a、b为常数，又设大数为x，小数为y，则有x+y=a，x-y=b构成方程组，解得x=(a+b)/2；y=(a-b)/2.

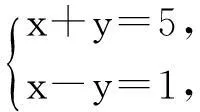
七年级和高一年级被试对问题4具体解法的统计结果如图5和图6所示.其中，使用文字代数解法(i)的七年级学生有4人、占13.3%，高一只有1人、占3.6%.高中生接触较长时间的简写代数和符号代数后，依然有少部分学生用文字叙述的方式解决该问题，说明少部分学生与学生整体认知水平的差异客观存在.

采用丢番图解法(ii)的七年级中仅有两2人，占比7%.究其原因，或许因为七年级学生的学习限于一元一次方程解法，对于二元一次方程组简写代数和符号代数的解法尚未系统学习，客观上存在困难.高一年级则没有人使用这种方法，他们更倾向于运用符号代数中的韦达法，整体而言符合高初中学生的认知发展规律和水平.

采用韦达解法(iii)的七年级学生数为0，高一年级有26人、占被试的92.9%.究其原因，或许因为七年级尚未学习解二元一次方程组，而高中生则在八年级系统学习了二元一次方程组的代数解法，采用韦达的符号代数解法相对驾轻就熟、便捷简单.

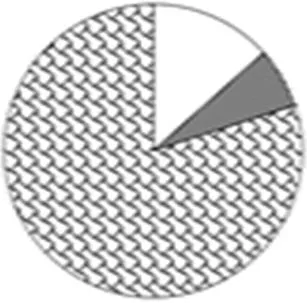
总体测试结果显示，七年级只有极少数(20%)的被试能用文字代数和丢番图法解决此题，但完全没有呈现符号代数的策略与方法，考虑到七年级学生尚未学习含两个未知量的方程，大多数被试不能解决此问题(即图5中的其他)，其表现与其认知发展水平一致.高一年级则有九成多的被试采用了韦达法成功解决问题，仅有一位学生未能解答此题.整体而言再次印证了随着学习经验的丰富、年级的递增，学生对字母表示数的认知和运用得到了显著提升和发展.

5结论与思考

“用字母表示数” 意义的演进伴随代数学3 000年的发展历程，经历了“表示特定的数→表示特定未知量→表示一类量(任意的已知量或未知量)”的发展过程；“用字母表示数”的发展并不是一帆风顺的，其发展路径是缓慢、艰辛而曲折的，总体呈螺旋上升.“用字母表示数”的功能在人类探索现实世界的数量关系中，经由从特殊到一般、由具体到抽象的反复认知与发展过程才得以逐步推进和完善.

测试结果表明，七年级和高一年级的学生虽然已经或多或少学习过符号代数，但是对应于“用字母表示数”3个发展阶段的3种方法仍然出现在这两个学段学生的解法中，为数不少的七年级和高一年级学生对“字母表示数”的理解与运用还停留在文字代数和简写代数阶段，对字母意义的认知水平大多停留在记数符号和未知量的水平.特别地，对于符号代数的“一类量”思想无论是七年级还是高一年级学生都存在认知困难，但是随着年级递增,尤其到高一年级，学生理解和运用字母表示“一类量”的思想解决问题的能力显著增强.

综上对比发现，中学生对“用字母表示数”的认知发展过程与历史上从文字代数到符号代数“字母表示数”意义演进的发展过程存在明显的相似性；学生对“用字母表示数”的认知发展与知识的历史演进过程一样，并非一帆风顺、而是呈循环反复、螺旋状缓慢上升，期间需要经历缓慢、曲折甚至反复的过程.研究结果印证和支持斯宾塞、波利亚、克莱因等人关于“个体知识发生过程必然遵循人类知识的发生过程”的历史发生原理，以及蒲淑萍、汪晓勤等人的相关研究结论.

以上研究结论启示我们，中学生对“用字母表示数”的理解与运用不会一蹴而就、一帆风顺，学生对于用字母表示的数“从已知数到未知量，从有个限数到无限个数、进而到一类量”每一个水平层次字母意义的认知、理解、运用，都是困难重重、甚至会互相干扰，常常表现为在具体的情景中涉及用字母表示数和解决问题时，容易陷入模糊不清和混乱胶着状态.因此，在教学中教师要深入了解和把握“用字母表示数”的历史发展脉络，以“记数符号→表示未知量→表示一类量”这3个认知水平的过渡环节为抓手，注重忆旧迎新，创设并借助丰富的问题情景，引领学生对新旧对象进行比较，为“用字母表示数”每一个认知水平层次的新知探究搭建相应的思维台阶，用适合学生认知规律的方式去设计和组织教学，以帮助学生跨越“历史障碍”，促进学生对“用字母表示数”的理解和掌握，提高课堂教学的质量和效率.

来自课堂实践的观察还发现，具备数学史知识的教师比较善于在知识的具体源头和抽象形式之间构建通往学生理解的桥梁.在一个缺乏数学史知识的教师眼中，往往只看到一堆形式化的符号与逻辑关系，因此难以从数学知识的历史发生视角、依据知识的发展规律来设计教学，促成学生的理解，难以引领学生透过数学史的独特视角把握其中蕴含的思维方法.可见数学史素养是每位数学教师必备的素养之一.

研究结果还在思想方法上启示着教材编写者，在教材的编写中应适度关注相关数学知识发生、发展的历史根源及变迁，适当呈现数学知识产生、建构的思想方法和背景，这样的背景、过程和方法对于学生体会与把握数学的本质无疑是有益的.如果教材编写时能够兼顾历史发生原理，这样的教材会给予师生的教与学更多启迪和智慧.

参考文献：

[1] 孙名鄂,李伯春,刘经国. 简明数学史[M]. 郑州：大象出版社，1998：75-81.

[2] 中华人民共和国教育部. 义务教育数学课程标准(2011版)[S].北京：北京师范大学出版社，2012：22,27-28.

[3] 蒲淑萍，汪晓勤. 学生对字母的理解：历史相似性研究[J]. 数学教育学报，2012,21(3):38-42.

[4] 虞琳娜. 在自然数的“表示”中感悟字母的含义——“用字母表示数”教学简录与思考[J].小学教学(数学版)2009(1)：33-34.

[5] 薛文叙. 关于学生对数和数的表示形式认知情况的案例研究[J].数学教育学报，2009(3)：1-6.

[6] 李文林.数学史概论[M].北京： 高等教育出版社，2002:65，129-130.

[7] 张映姜,陈美英,李晓培,等.数学的历史文化赏析[M].长沙：湖南师范大学出版社，2013：32.

[8]CLEMENTJ.Algebrawordproblemsoultions:thoughtprocessesunderlyingacommonmisconception[J].JournalforResearchinMathematicsEducation,1982,13:16-29.

[9]SPENCERH.Education:intellectual,moral, &physical[M].NewYork:Hurst&Company, 1862,35.[10]KLINEM.Thenncientsversusthemoderns:anewbattleofthebook[J].MathematicsTeacher,1958,51(6)：419-426.

收稿日期：2015-08-30

基金项目：国家级大学生创新创业训练项目(1427815032)；广东第二师范学院教授博士专项科研项目(2013ARF21)

作者简介：陈静安, 女，云南昆明人,广东第二师范学院数学系教授.

中图分类号：G 633.6

文献标识码：A

文章编号：2095-3798(2016)03-0090-06

A Study of Historical Parallelism on Middle School Students’UnderstandingoftheLettersRepresentingNumbers

CHENJing-an1，HUANGQi-liang1，FANJia-yun2，WUHong-qin1

(1.DepartmentofMathematics,GuangdongUniversityofEducation,Guangzhou,Guangdong,510303,P.R.China;2.LiupanshuiNo.7MiddleSchool,Liupanshui,Guizhou, 555300,P.R.China)

Abstract:"Letters Represent Numbers" is an important part of middle school mathematics, and also a significant stage for middle school students to learn the transition from rhetorical algebra to symbolic algebra. Sample tests for the Seventh Grade students and Senior Grade One students on their understanding of "Letters Represent Numbers" have been conducted. The results indicated that the development process of students′understanding of "Letters Represent Numbers" is similar to the historical evolvement process of the meaning of "Letters Represent Numbers" itself. Such similarity is essential to assist the preparation of teaching method and learning materials that are related to the topic of "Letters Represent Numbers".

Key words:to represent numbers in letters; rhetorical algebra; syncopated algebra; symbolic algebra; historical parallelism