关于半线性方程div(|Du|p-2Du)=f(|x|,u)的有界正整解

许兴业

(广东外语外贸大学 南国商学院公共课教学部, 广东 广州 510545)



关于半线性方程div(|Du|p-2Du)=f(|x|,u)的有界正整解

许兴业

(广东外语外贸大学 南国商学院公共课教学部, 广东 广州 510545)

摘要:研究形如div(|Du|p-2Du)=f(|x|,u)的半线性椭圆型方程的有界正整解问题，建立了2个有界正整解的存在性定理.

关键词:半线性椭圆型方程；有界正整解；相对紧；连续映照；不动点定理

0引言

本文运用Schauder-Tychonoff不动点定理研究一类形如

div(|Du|p-2Du)=f(|x|,u)

(1)

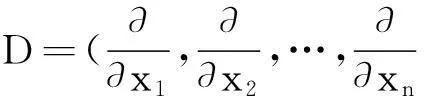
1主要结果

定理1设f(r,u)满足：

(Ⅰ)f(r,u)关于u∈R+是不减函数；

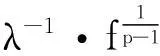
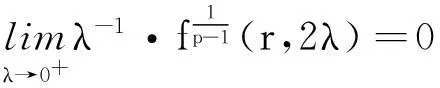
(2)

(Ⅲ)存在常数c>0使

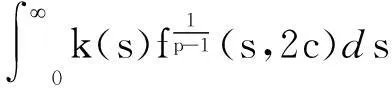
(3)

则方程(1)存在无穷多个有界正整解u(x).其中

证明令u(x)=y(|x|)，则方程(1)可归结为常微分方程的初值问题：

(4)

其中φp(y)=|y|p-2y,η为待定常数.从而初值问题(4)的解等价于如下积分方程的解.

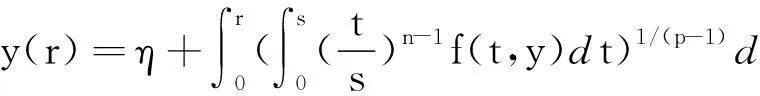
(5)

从而转到讨论积分方程(5)的可解性.由(Ⅱ)知

k(s)f1/(p-1)(s,2λ)·λ-1≤k(s)f1/(p-1)(s,(2c)·c-1,λ≤c.

其中c是(Ⅲ)中出现的常数，且对每一s∈(0,),当λ→0+时有

k(s)f1/(p-1)(s,2λ)·λ-1→0.

由(Ⅲ)知

于是由Lebesgue控制收敛定理得

(6)

由(6)知可以选择充分小的常数η>0使得

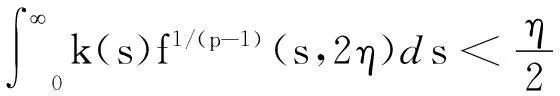
(7)

记C1[0,∞)是定义在[0,∞)上的所有连续可微函数作成的空间，依通常的方法引入C1[0,∞)的拓扑，作集合

G={y∈C1[0,)|η≤y(r)≤2η,0≤y′(r)≤(η/2)1/(p-1),r≥0}，

则G是C1[0,)的闭凸子集.定义映射Φ:G→C1[0,)如下：

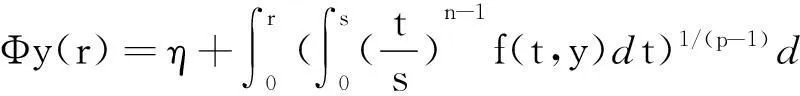
(8)

在这里补充定义：

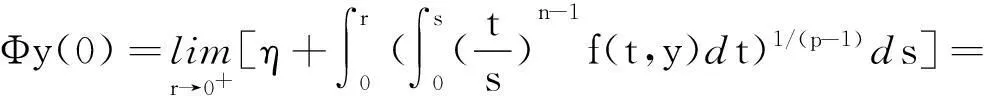
下面分三个命题证明映射Φ满足Schauder-Tychonoff不动点定理的条件.

命题1Φ:G→G.

对∀y∈G，由(7)、(8)得

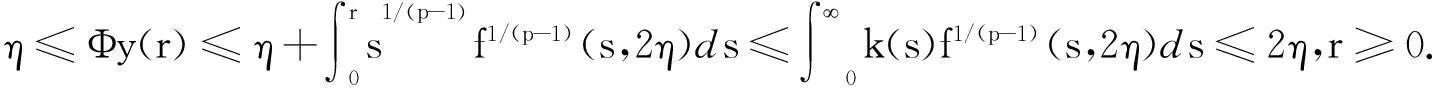
(9)

进一步由(8)知当r>0时

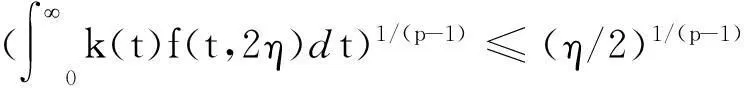
(10)

注意到(10)式

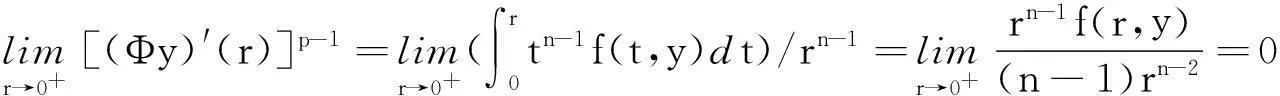
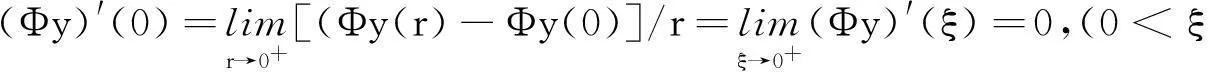
0≤(Φy)′(r)≤(η/2)1/(p-1),r≥0.

(11)

所以ΦG⊂G.

命题2Φ是连续映射.

设yi∈G(i=1,2,…)且依C1[0,)的拓扑yi收敛于y.对∀r∈[0,)由(8)、(10)式得

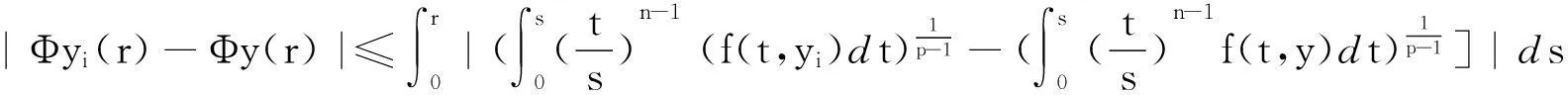
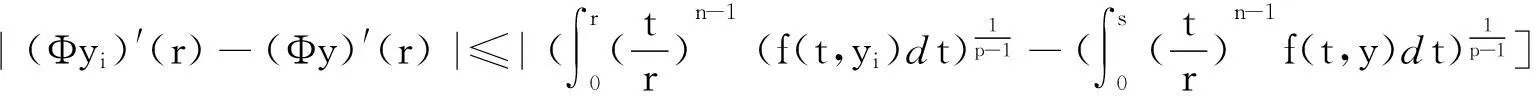
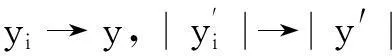
命题3ΦG是相对紧的.

先证{Φy(r)|y∈G}与{(Φy)′(r)|y∈G}在[0,)的任一紧子区域[0,M]一致有界且等度连续.事实上，对∀[0,M]⊂[0,),{Φy(r)|y∈G}与{(Φy)′(r)|y∈G}在[0,M]上的一致有界性以及{Φy(r)|y∈G}在[0,M]上的等度连续性从(9)和(11)即可以看出.于是需证明{(Φy)′(r)|y∈G}在[0,M]上的等度连续性.由(10)式当r>0时有

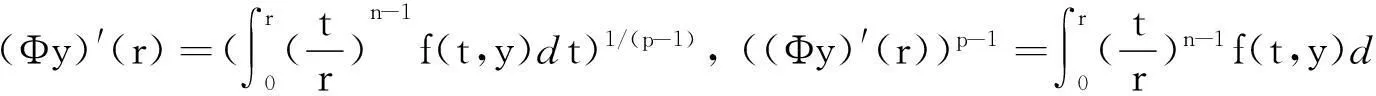
注意到f(r,u)≥0,有φp(y′)=|y′|p-2·y′=(y′)p-1，从而

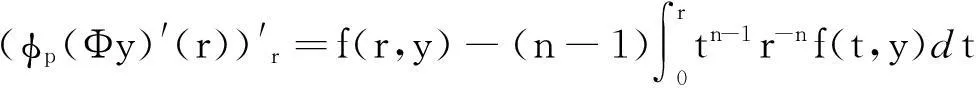
(12)

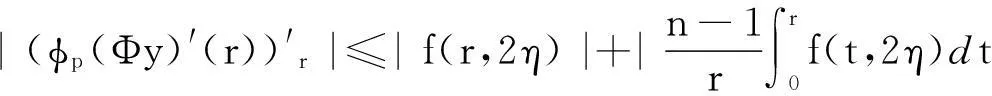
(13)

由(12)式得

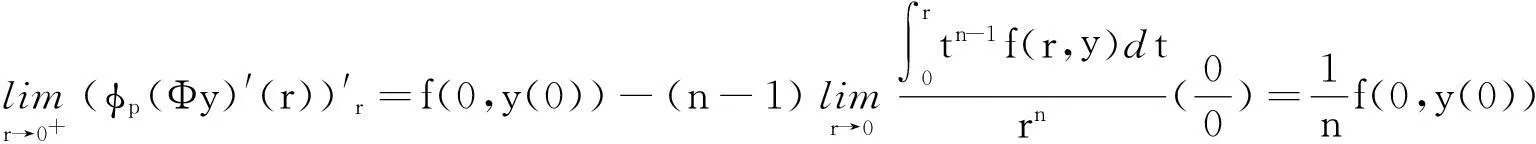
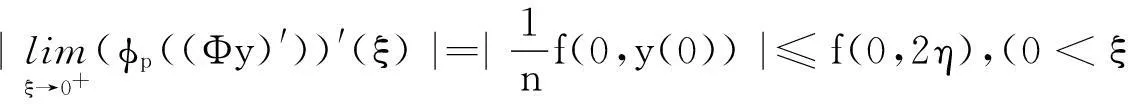
于是(13)式对任意r≥0成立.从而在[0,M]上对(φp((Φy)′(r)))′有估计式:

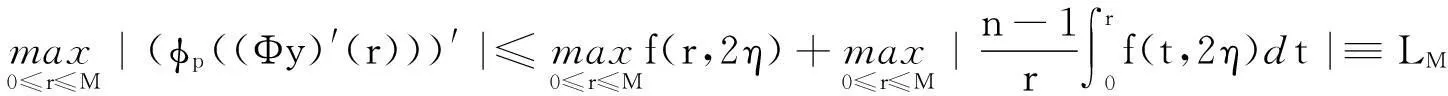
从而在[0,M]上有估计式|φp(Φy) ′(r1)-φp(Φy) ′(r2)|≤LM|r1-r2|,r1,r2∈[0,M]，即

|((Φy) ′)p-1(r1)-((Φy)′)p-1(r2)|≤LM|r1-r2|,r1,r2∈[0,M]，故有

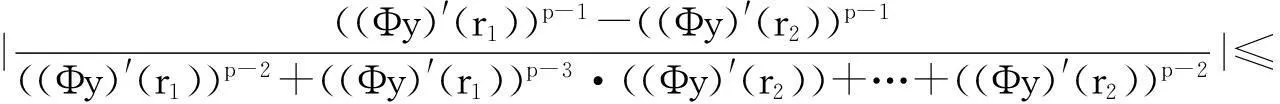
这就证明了{(Φy) ′(r)|y∈G}在[0,M]上是等度连续的.故对[0,∞)的任一紧子区间[0,M]，依C1[0,∞)的拓扑能用Ascoli-Arzela定理[7].

要证明ΦG在G中是相对紧的，即要证ΦG中任一序列{(Φyi)(r)}必包含一个子序列，该子序列依C1[0,∞)的拓扑收敛于中G的一个元素，我们只要对区间列[0,M1]⊂[0,M2]⊂…⊂[0,Mj]⊂…,(其中Mj→,当j→时)逐次利用Ascoli-Arzela定理，并采用“取对角线子列”手续即可完成.

上面3个命题证明了Schauder-Tychonoff不动点定理[8]的条件全部满足，所以Φ存在不动点y∈G，即y就是方程(8)的解，且依G的定义知y满足η≤y≤2η，从而也就证明了方程(1)存在有界正整解u(x)=y(|x|),x∈Rn.

选择ηk,(k=1,2,3,…)满足(7)式，且使诸区间[ck,dk]互不相交，其中ck=ηk,dk=2ηk，则对每一k，由上面的证明知方程(1)存在有界正整解uk(x),k=1,2,3,…且ck≤uk(x)≤dk，所以方程(1)存在无穷多个有界正整解.

定理1′设除了f(r,u)满足定理1中的假设(Ⅰ)、(Ⅲ)外，还满足

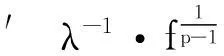
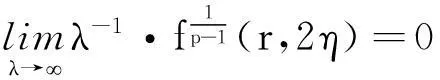
(2)′

则方程(1)存在无穷多个有界正整解u(x).

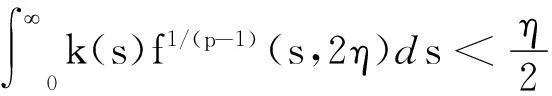
定理2设f(r,u)满足：(Ⅰ)f(r,u)关于u∈R+=[0,)是不增函数；

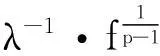
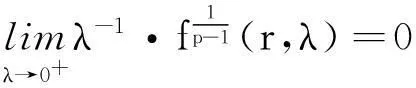
(14)

(14)′

(Ⅲ)存在常数c>0使

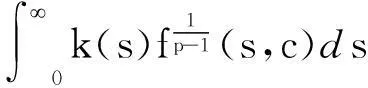
(15)

则分别在假设(Ⅰ)、(Ⅱ)、(Ⅲ)或(Ⅰ)、(Ⅱ)′、(Ⅲ)下方程(1)存在无穷多个有界正整解u(x).其中

证明同定理1完全类似，略.

3例子

例1考察方程

div(|Du|p-2Du)=a(|x|)uα,x∈Rn,n≥2,α>0，p>1.

(16)

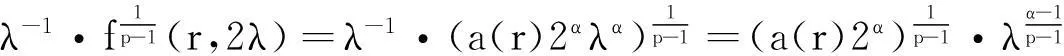
(17)

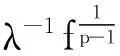
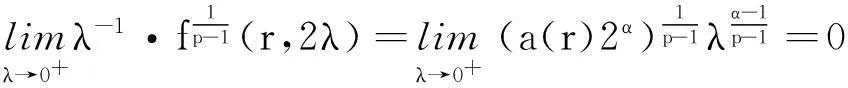
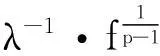
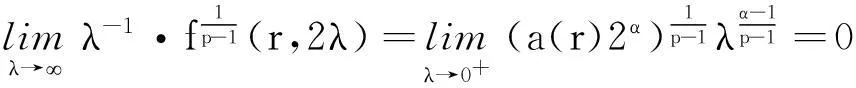
参考文献：

[1]KUSANOT,SWANSONCA.Positiveentiresolutionsofsemilinearbiharmonicequations[J].HiroshimaMath,1987,17(1):13-28.

[2]KAWANON,KUSANOT,NAITOM.OntheellipticequationsΔu=Φ(x)uγinR2[J]. Proc Amer Math Soc,1985, 93:73-78.

[3] 叶常青.一类奇异非线性双调和方程正整解[J].数学物理学报，2001,21A(1):138-144.

[4] XINGYE X， BICHENG Y,DEBNATH L. Positive entire solutions of nonlinear polyharmonic equations in R2[J].Applied Mathematics and Computation,2002,126:377-388.

[5] 许兴业.一类拟线性椭圆型方程正的径向对称整体解的存在性[J].广东第二师范学院学报,2015，35(5):48-51.

[6] 许兴业.一类奇异拟线性椭圆型方程的正整解.韶关学院学报(自然科学)，2015,36(12):1-4.

[7] ADMAS R A. Sobolev spaces[M]. Boston：Acamdemic Press,1975.

[8] EDWARDS R E. Functional analysis[M]. New York: Rinchart and Winston,1995.

收稿日期：2016-03-22

基金项目：广东外语外贸大学南国商学院校级重点科研课题资助项目(16-005A)

作者简介：许兴业，男，广东普宁人，广东外语外贸大学南国商学院公共课教学部教授.

中图分类号：O 175.25

文献标识码：A

文章编号：2095-3798(2016)03-0039-05

The Bounded Positive Entire Solutions to the Semilinear Equations Such as div(|Du|p-2Du)=f(|x|,u)

XU Xing-ye

(Department of Public Course Teaching, South China Business College, Guangdong University of Foreign Studies, Guangzhou, Guangdong, 510545, P.R.China)

Abstract:This paper aims to study the problem of bounded positive entire solutions to semilinear equations such as div(|Du|p-2Du)=f(|x|,u), and has established two existence theorems of bounded positive entire solutions.

Key words:semilinear elliptic equations; bounded positive entire solutions；relative compactness; continuous mapping; fixed point theorem