爱因斯坦的等效原理在实际问题中的应用

惠　萍，朱　兴

(广东第二师范学院 物理与信息工程系, 广东 广州 510303)



爱因斯坦的等效原理在实际问题中的应用

惠萍，朱兴

(广东第二师范学院 物理与信息工程系, 广东 广州 510303)

摘要:形象地描述爱因斯坦《广义相对论》中的等效原理，引入引力场的概念. 通过非惯性系中的浮力现象和非惯性参照系中的力的平衡的案例，来描述爱因斯坦《广义相对论》中的等效原理在这些实际问题中的应用. 在非惯性系中，应用了爱因斯坦的等效原理，使一些在惯性参照系看起来很复杂的问题变得很容易解决.

关键词:广义相对论；等效原理；非惯性参照系

0引言

1915年12月2日爱因斯坦发表了《广义相对论》，在纪念这篇论文发表100周年的日子，引力波又被探测到，广义相对论被认为是人类认识大自然最伟大的成果，为了纪念这一伟大理论的诞生，最近也有一些文章介绍了广义相对论的发展历程和爱因斯坦广义相对论的伟大贡献[1-6]，包括爱因斯坦提出的惯性质量同引力质量相等、光速不变原理、广义相对性原理、马赫原理和等效原理，说明了等效原理在分析引力场中时间延缓, 星光谱线的引力红移和光线偏转等问题上的应用. 在人们脑海里，觉得相对论很伟大，但就像引力波一样，人们对相对论却看不见，摸不着，它好像离我们很遥远，因为它不太容易被理解和认识，因此人们对其也就敬而远之. 如果能把广义相对论的原理用于解决我们身边的生活实际问题就好了，为了这个目的和科学普及，作者怀着对爱因斯坦最崇敬的心情写了这篇短文，一是表达对爱因斯坦最崇高的敬意，二是向老师和学生推广相对论基本原理的应用. 因为，无论在高中物理和大学的普通物理中，爱因斯坦广义相对论的等效原理都没有介绍给学生，更谈不上应用. 众所周知，任何科学成果都是为人类服务的，我们应循序渐进地、深入浅出地把《广义相对论》的内容介绍给青少年，让他们尽早接触近代物理思想，启发青少年的思维，培养他们的创造性思维能力. 爱因斯坦16岁就开始思考牛顿时空观的缺陷，26岁发表狭义相对论，36岁发表广义相对论. 这个例子让我们坚信青少年的思维能力和创造能力的培养具有强大的空间. 本文谈谈爱因斯坦的等效原理在实际问题中的应用.

1爱因斯坦的等效原理

在中学或大学物理中，我们习惯在惯性参照系解题，因为在非惯性参照系中，牛顿定律不适用；但在实际生活中，非惯性参照系的物理问题更为普遍，老师和同学们都必须面对和解决. 为了解决非惯性参照系的物理问题，首先介绍一下爱因斯坦的等效原理.

为了理解等效原理，先做实验一，如图1所示，密闭装满水的透明玻璃管里放一乒乓球，乒乓球直径小于玻璃管的内径，将玻璃管固定在转盘上，转盘静止时，乒乓球刚好在玻璃管的中间，当圆盘绕轴OO′轴旋转时，问：乒乓球最后停留在什么位置？

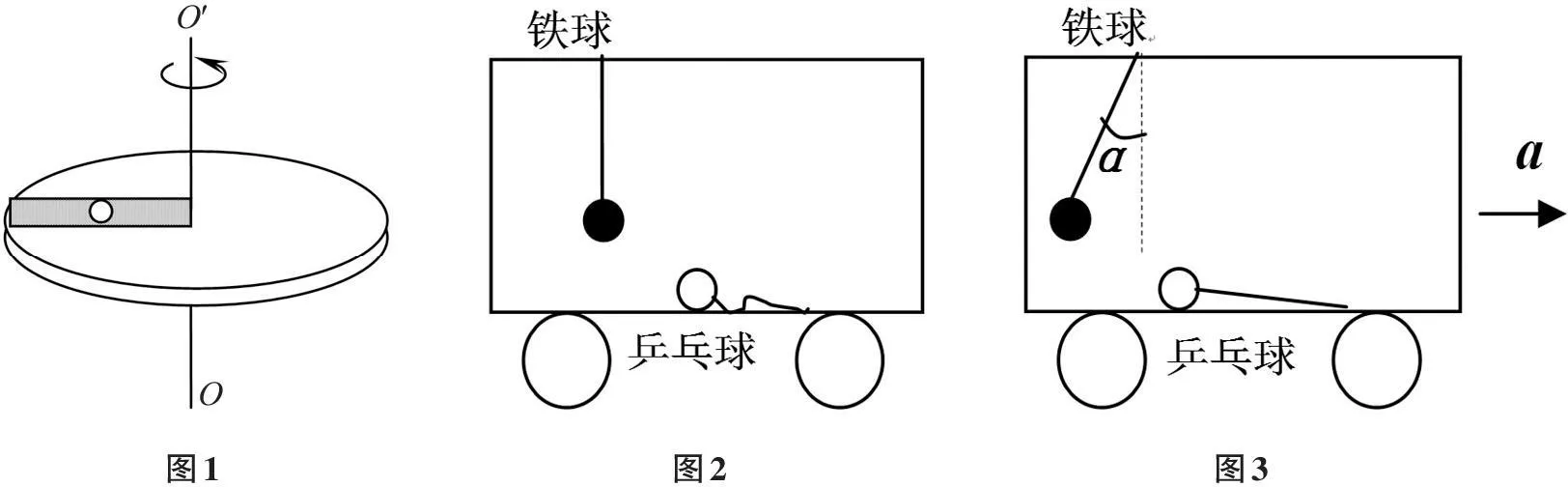
图1图2图3O′O

按照生活经验，学生可能会猜想：乒乓球受到惯性离心力的作用，沿着玻璃管向外移动.而实验结果是：乒乓球沿着玻璃管向轴方向移动，靠在轴的位置停住. 对这个实验现象，解释起来很费劲，也很难解释清楚. 而用爱因斯坦的等效原理就很容易回答这个问题了.

爱因斯坦的等效原理：在无限小的体积中均匀的引力场完全可以代替加速运动的参照系. 为了说明这个原理，再做实验二，设重力加速度为g，在相对地面静止的升降机里用一弹簧秤测量一物体的重量为1.0N，当升降机以加速运动a=g向上运动时，观察到升降机里的弹簧秤重量示数为2.0N，假如升降机里的人不知道升降机已经启动，看到弹簧秤重量示数为2.0N时，还以为地球的引力增加了一倍. 这个例子说明，以升降机为参照系，以加速运动a=g向上运动的升降机(非惯性参照系)等效一个向下的引力场(重力场).这就是爱因斯坦提出的封闭空间的说法，在一封闭空间中的观察者，不管用什么方法也无法确定他究竟是静止于一个引力场中，还是处在没有引力场却在作加速运动的空间中， 这也是解释等效原理最通俗的说法. 再直观地说：在任何一个时空点上 ，加速度为a的匀加速运动参考系与重力加速度为a的重力场是等价的，在这个实验中，重力场的方向与加速度a的方向相反.

等效原理是广义相对论的第一个基本原理，也是整个广义相对论的核心. 爱因斯坦于1911年注意到这一规律，1915年正式以原理的形式提出来. 现在尝试用这个基本原理解释和解决非惯性参照系中的一些物理现象和物理问题.

2爱因斯坦的等效原理在实际问题中的应用

2.1非惯性系中的浮力现象

下面应用等效原理，解释实验一(如图1所示)的物理现象，圆盘旋转有向心加速度，在这个非惯性系中，相当于圆盘上的物体受到一个沿着径向向外的引力场，水和乒乓球受引力场的作用，使得水沿径向向外的压强越来越大，乒乓球除了受引力场的作用外，还受到沿着径向向内浮力的作用，因为乒乓球所受到的引力场所产生的浮力大于所受到的引力场的引力，乒乓球一定是向OO′轴方向运动，直到靠近轴的位置被轴挡住. 用爱因斯坦的等效原理就很容易回答这个问题了.

接下来做实验三，如图2和图3所示，在封闭车厢的顶部和底部，分别用细线连一铁球(质量为M)和一乒乓球(质量为m). 以车厢为参考系观察下列实验现象并回答问题：

(i)如图2所示，首先让车厢相对于地面静止，由于重力作用，铁球自然下垂，乒乓球在车厢底面不动. 当车厢以加速度a向右运动时，如图3所示， 连接铁球的细线向左偏转α度角，乒乓球在车厢底面向左滑动把线拉直. 问偏转角α是多少？乒乓球所受到细线的拉力是多少？

用等效原理来解释上述现象：以加速a向右运动的车厢是非惯性参考系，以运动的车厢为参照系，当车厢里的其他物体的状态稳定时，铁球如同受到一个向左的引力场的作用，所受引力大小为Ma，铁球同时受垂直向下的力Mg和向左的引力Ma作用，因此α=arctan(a/g)，乒乓球所受垂直向下的重力和厢底对它支持力平衡，因此，乒乓球所受到的细线的拉力(近似水平方向)等于乒乓球受到向左的引力场的引力ma.

(ii)如图4所示，保持车厢相对于地面静止，使车厢充满水，在重力场作用下，铁球仍然下垂，乒乓球却浮起. 问：当车厢以加速度a持续向右运动的过程中，如果车厢里连接铁球的细线向左偏θ度角，问θ角与图3的α角哪个大？连接乒乓球的细线如何偏转？细线偏转度角是多少？

很多学生凭感觉，认为水有阻力，猜想θ<α；认为乒乓球有惯性，连接乒乓球的细线会向左偏转，然而事实并非如此. 我们用等效原理来解决上述问题：如图5，当车厢里的水达到平衡时，以加速a向右行运动的车厢是非惯性参考系，我们可以用一个向左的引力场(引力场加速度为a)来代替非惯性参考系，铁球受垂直向下的重力Mg和向左的引力Ma. 同时铁球受向上的浮力和向右的浮力分别为 ρ水V铁球g和ρ水V铁球a， 由于铁的密度大于水的密度，所以，系铁球的细线仍然以θ=arctan(a/g)度向左偏，即θ=α. 同理，由于乒乓球所受浮力的合力大于它所受到的引力的合力，连接乒乓球的细线发生偏转，角度为-arctan(a/g).这一现象如果用惯性力(假想力)来解释，无法解释清楚，而且会让学生产生疑问：一个假想力怎么能在液体里产生压强差？文献[7]在讨论这个问题时，试图解释乒乓球的“反常”现象 ，但是，由于液体从一个平衡态变化到另一个平衡态的过程很复杂，最终还是没有解释得很清晰.

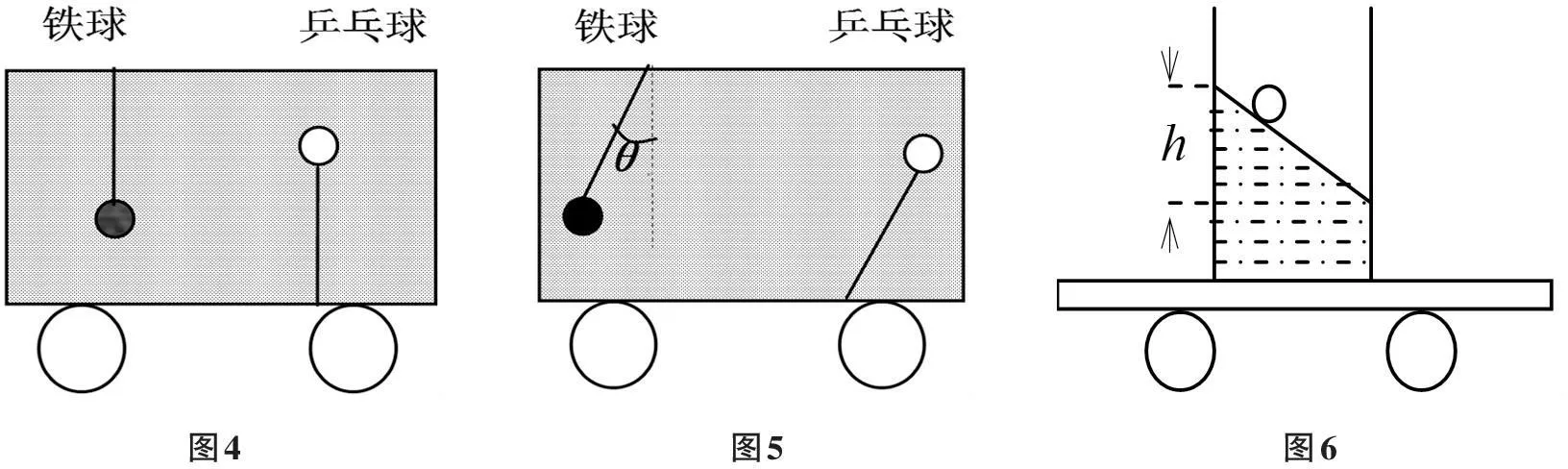
图4图5图6

实验四，如图6所示，水平地面有一小车，固定一个盛水的鱼缸，当小车以加速度a向右运动，求水面倾斜角和水箱里左边h深度处的压强.

利用爱因斯坦的等效原理，以运动的小车为参考系，水除受重力外，还受到向左的引力场的引力，引力加速度为a，当小车里的水达到平衡时，水面一定垂直两个引力合力的方向，于是得到水面倾斜角为θ=arctan(a/g). 合引力场的引力加速度大小为：

在水中，平行于水面的任何一个面上的压强都是相等的，所以水箱里左边h深度处的压强为

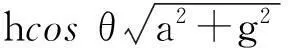
由此我们知道，在水中，平行于地面的任意平面上的压强不再都相同了.

反过来思维，我们可以做下面的题目，如图6所示，在水平地面上有一小车，透明鱼缸里的水表面相对于地面倾斜角为θ，请问小车做的什么运动？乒乓球在水面做什么运动？

答：小车向右做加速度运动，加速度为

a=gtanθ,

乒乓球在水面上不动.

下面留一思考题给读者：圆柱型桶里装半桶水，使桶绕其圆柱中心轴快速顺时针旋转，当水面稳定时，水面形成什么形状，有兴趣的读者可以尝试计算水中不同位置的压强.

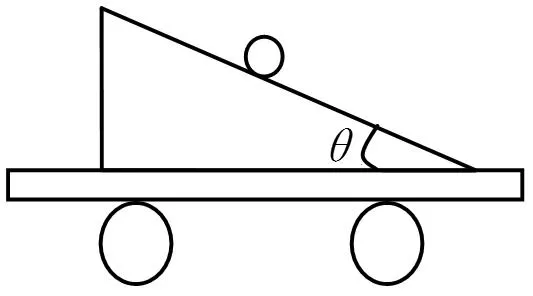
图7

2.2非惯性系中的力的平衡

实验五，如图7示，倾斜角为θ的三角形木块固定在一小车上，一个质量为m的小球在斜面上不动，以小车为参考系，问小车向右运动的加速度a是多少？

利用爱因斯坦的等效原理，以小车为参考系, 小球除受重力mg外，还受到向左的引力场的引力ma , 二者合力方向垂直斜面，

tanθ=ma/mg,

a=gtanθ.

以上例子告诉我们，惯性系中的一些加速运动问题，可以转换成非惯性系中的力的平衡问题，使复杂的问题变得简单. 希望更多的同学和老师在处理非惯性系问题时从中得到启发.

参考文献：

[1] 赵峥. 爱因斯坦与广义相对论[J].物理,2015,44(10):646-656.

[2] 方在庆.爱因斯坦通往广文相对论之路[J].科学,2015,67(5):9-14.

[3] 赵峥.爱因斯坦与广义相对论的诞生——纪念广义相对论发表100周年[J].大学物理,2015,34(11):1-5.

[4] 向义和.浅谈广义相对论的创立之一 等效原理的发现与应用[J].大学物理,2014,33(11):28-33.

[5] 赵峥.广义相对论的几个问题[J].大学物理,2011,30(5):14-19.

[6] 郝刘祥.等效原理与引力的规范理论[J].自然科学史研究,2011,30(2):241-255.

[7] 郑太玉，王文涛. 高观点下的中学物理探讨[M]. 北京：高等教育出版社，2011:36.

收稿日期：2016-02-27

基金项目：国家自然科学基金资助项目(10874122 )

作者简介：惠萍，女，吉林通化人，广东第二师范学院物理与信息工程系教授.

中图分类号：O4-3

文献标识码：A

文章编号：2095-3798(2016)03-0107-04

The Applications of Einstein EquivalencePrincipleinPracticalProblems

HUIPing,ZHUXing

(DepartmentofPhysicsandInformationEngineering,GuangdongUniversityofEducation,Guangzhou，Guangdong, 510303,P.R.China)

Abstract:We vividly describe the equivalence principle in Einstein’s "general theory of relativity", and introduce the concept of gravitational field. Through the cases of buoyancy phenomenon and force balance in non-inertial system, we describe applications of the equivalence principle of the Einstein’s "general theory of relativity" in these practical problems. In the non-inertial system, using the Einstein equivalence principle can help solve some problems more easily, which look more complicated in inertial system.

Key words:general relativity; equivalence principle; non-inertial reference system