基于创新型人才培养的大学数学课程改革研究——以高等数学实验教学为例

辛冬梅， 闫志来

(1.广东第二师范学院 数学系， 广东 广州 510303；2.广州中医药大学 经济管理学院， 广东 广州 510000)



基于创新型人才培养的大学数学课程改革研究
——以高等数学实验教学为例

辛冬梅1， 闫志来2

(1.广东第二师范学院 数学系， 广东 广州 510303；2.广州中医药大学 经济管理学院， 广东 广州 510000)

摘要:创新是引领发展的第一动力.在高等数学教学中引入数学实验，发挥基础实验和探索、应用及综合建模实验的作用，对大学数学课程进行改革，可培养创新型人才.高等数学教学中开展数学实验的措施：要保持高等数学知识体系结构，做好课程设置及管理，改进教学内容、方法，制作调查分析对比表，制定科学的考核方式，达到创新知识、培养学生的综合素质和创新能力、培养创新型人才的目的.

关键词:创新型人才；高等数学；数学实验；课程改革

0引言

“创新是引领发展的第一动力”.2015年两会期间，习近平总书记在参加上海代表团审议时提出了这一重大论断[1].党的十八大以来，创新驱动发展战略在神州大地落地生根，引领中国经济不断向前.十八届五中全会提出的“创新、协调、绿色、开放、共享”的五大发展理念.创新发展居于首要位置，是引领发展的第一动力.李克强总理在2015年《政府工作报告》中提出“大众创业、万众创新”，激发了人们的创业、创新热情.今年将“四众”(众创、众包、众扶、众筹)写入《政府工作报告》，显示了政府对创业创新支撑平台建设的高度重视.在今年的《政府工作报告》中，“创新”一词被提到了59次，几乎等于前两年报告中被提到次数之和.

钱学森教授在1989年就指出了计算机对数学教学的深刻影响，提出了理工大学的数学课要改造一番，要实现计算机与课程教学的紧密结合，提倡计算机的模拟与实验.中国科学院王元院士也强调：计算机和数学软件的使用对培养工科学生的数学学习能力十分重要[2].许多科学家和数学家都强调把计算机和数学软件作为教学手段和工具，融入到大学数学教学， 突出学生的主动参与性，提高学生的探索能力、实践能力、团队协作能力及综合素质是培养创新型人才的重要途径.1985年，美国在大学生中举行首届数学建模竞赛，随后越来越多国家开展这类竞赛.我国从1989年起也组织队伍参加美国大学生数学建模竞赛[2].中国数学建模竞赛于1992年开始举办[2]，1994年由国家教委高教司和中国工业与应用数学学会联合主办，得到中国数学会、各地数学会和高校的支持，为培养学生的创新能力开辟了途径，对高校数学教育改革产生了良好的影响.

1创新型人才所具有的素质

创新型人才富于开拓性，具有创造能力，能开创新局面，对社会发展做出创造性贡献的人才.通常表现出灵活、开放、好奇的个性，具有精力充沛、坚持不懈、注意力集中、想象力丰富以及富于冒险精神等特征.具体有以下几个特征[3]：有很强的好奇心和求知欲望；有很强的自我学习与探索的能力；在某一领域或某一方面拥有广博而扎实的知识，有较高的专业水平；具有良好的道德修养，能够与他人合作或共处；具有观察、实验、类比、归纳、演绎、抽象与概括等重要的数学素质，具有较强的理解与领悟能力、逻辑分析与推理能力、灵活应变与创造能力；锲而不舍、坚韧不拔的意志和毅力.

2传统高等数学教学存在的问题

2.1偏理论推导和演算，少思想方法和应用

传统高等数学教学多采用“从概念到定理，再到证明、例题、习题”的严谨、条理的注入式教学模式，教师花费大量的时间用于定理的推导和例题的演算等定性知识的展现，缺乏思想方法、事物规律的揭示，忽视了很多数学概念和知识是来源于生活实践和现实世界的.事实上，在教材中有许多经典模型被用于概念的提出，例如高数上册中，引入经典变速直线运动的瞬时速度模型，给出导数概念；引入变速直线运动的路程模型，给出定积分概念.让学生感觉到数学是有活水源头的，是我们熟悉的自然生活，那些看似枯燥无味的概念、定理和公式并非无木之本、无水之源，也不是凭空想象出来的，而是有其现实背景和来源的，与我们的生活密切相关，是从社会生活实践中抽象出来，用于解决更多实际问题的.学生沿着数学知识的形成过程，自然体悟数学知识的合理性.但在教学中，经典模型往往成为概念、定理引入的敲门砖，用后就被弃之不理，转向重复枯燥的套公式演算模式，没有后续的将所学数学知识进一步在实际模型中升华.

2.2数学建模所起作用有限

目前，数学建模大赛极大地推动了数学建模在高校广泛开展，调动了学生“学数学，用数学”的热情，通过数学竞赛，使学生将课堂知识进一步升华提高，看到了所学知识的不足和局限，从而产生强烈的主动求知欲，增强了学习兴趣，提高了“学数学，用数学”的创新意识.但从各高校开展数学建模的现状来看，数学建模竞赛仅限于部分优秀学生参加，绝大多数学生并未参与，而且参加的学生也仅限于竞赛时间段内接触数学建模，很多同学不知如何入手.虽然有的学校把数学建模和数学实验作为选修课，但受到指导建模的老师少、条件有限等限制，数学建模对培养学生应用数学能力的作用非常有限.如果不把数学建模、数学实验思想融入到数学课中，数学建模、数学实验也无法充分发挥培养创新人才的作用.

2.3教师知识更新、整合不够

数学实验融入数学教学中要求将计算机技术、数学软件穿插于教学过程中，并结合当前出现的最新的社会环境、经济、医疗、生物、物理、化学、天文、军事等实际问题，根据所学数学知识分析问题，建立数学模型，利用所学计算机和数学软件知识进行编程、计算、绘图,最终解决问题，得出结论并揭示问题的本质，给出建设性建议，进一步预测、猜想新的成果，从而提高学生分析问题、解决问题、提出问题的能力及创新能力.这对教师运用综合知识能力有一个更高的要求，特别是对于基础课单一知识结构的教学教师而言，要掌握计算机技术和至少一门数学软件，是对教师的一个挑战.要把数学实验、数学建模思想融入到教学中，就需要教师不仅具有较强的数学专业知识，更要具备丰富的综合知识应用和解决实际问题的能力，迫使教师了解、掌握更多的综合知识，并和各学科教师整合知识，及时了解更新前沿知识、提高业务能力和科研能力.

3数学实验引入高等数学在培养创新型人才所起的作用

数学实验是以实际问题为载体，把数学知识、数学建模、数学软件和计算机有机结合起来，强调学生的主体地位，在教师引导下查阅文献资料，用所学的数学知识和计算机技术，借助适当的数学软件，如常用的Mathematical、MATLAB来分析解决一些实际问题，并撰写实验报告或论文，使学生得到全面锻炼，从而增强学生学习数学的兴趣，培养学生的主动探索精神、综合应用能力和创新意识.

3.1发挥基础实验作用

基础实验[4]主要以数学软件命令的学习和应用为主，注重基本数学运算和验算的实验，包括函数极限、导数微分以及积分、级数运算和验算等基础实验，还有函数平面、立体作图实验、函数逼近实验、方程求解实验等内容.通过基础性实验教学，学生掌握基本的数学软件函数命令的使用和简单编程技术，用计算机技术和数学软件来观察、了解数学概念、定理知识的来龙去脉以及知识间的相互联系，体验、发现、总结和应用数学的规律，为后续的探索、应用、综合实验做准备.

例如求和级数这部分实验，基础实验目的：掌握Mathematical数学软件中求有限和及数项级数和的命令；验证级数敛散性.

例1(计算问题)印度年轻的传奇数学家拉马努金提出了一个级数描述圆周率p的公式

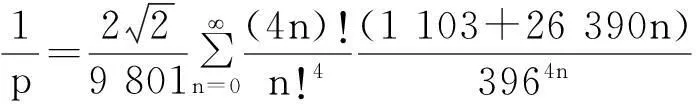
试用这个公式计算圆周率p的近似值，要求结果精确到小数点29位[5].

[程序]：P1[n_]∶=2Sqrt[2]/9801*Sum[(4k)!

*(26390k+1103)/396^(4k)/(k!)^4,{k,0,n}]

//将以上表达式右端的导数定义为P1[n]函数，其中n为求和的项数.

s=N[1/P1[2],29]; //N[]函数保留小数点29位

Print["s=",s] //输出s的数值

s=3.1415926535897932384626490657

Print["err=",N[p-s,29]] //输出精确p值和本表达式计算的p值之间的误差

err= -5.6824*10-24

利用数学软件Mahtematical或Matlab中计算级数和的函数Sum[]和平方根函数Sqrt[] 得出这个公式计算p值的准确率非常高，并增减参数n的值来给出不同的误差值下的p值这个例题是典型的应用数学软件命令来进行复杂计算的基础实验.

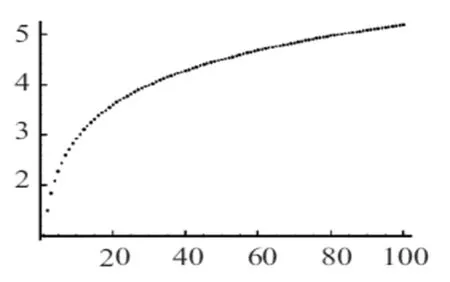
图1　调和级数散点图

s[n_]∶=NSum[1/k,{k,1,n}]

t=ListPlot[Table[{k,s[k]},{k,1,100}]，PlotSyle→PointSize[0.01]]

通过离散点图1观察验证得出调和级数是发散的.

3.2发挥探索、应用实验以及综合建模实验的作用

探索实验是以算法构造和计算机编程为目的，注重利用所学知识、具有探索实验特点的实验；应用实验是注重解决实际问题的实验，综合建模实验是数学实验的核心部分，是在基础实验的基础上培养学生的主动性、探索性、应用性、合作性、创新性.要求学生具备扎实的数学基础知识和计算机编程技术以及熟练的数学软件操作.在前半学期，主要以基础实验、探索实验、应用实验为主；后半学期，在前期实验的基础上逐渐过渡到综合实验，学生以3-5个人为一组，利用课内外时间围绕所给设计题目，有目的的查阅、学习相关知识和文献资料，通过团队的合作实验、讨论等形式，用实验方法分析问题、建立数学模型、求解模型、结果分析，进一步归纳、猜想新结果.在教师的指导下，撰写实验报告，最后通过答辩完成课题的设计过程.这种新模式，使得学生在实验中学习、探索、发现数学规律及应用，既巩固了对理论知识的理解，又培养了学习的主动性、创新性、团队合作精神，增强了学生独立思考，利用所学数学思想方法解决实际问题的能力，达到培养创新型人才的教学目的.

从例2的散点图上发现它与自然对数lnx非常接近，将自然对数lnx与散点图画在一起比较.

[程序]: p=Plot[Log[x],{x,1,100}]Show[t,p]N[s[100]-Log[100]] 0.582207N[s[1000]-Log[1000]] 0.577716N[s[10000]-Log[10000]] 0.577266

图2　调和级数与ln x　　　　比较图

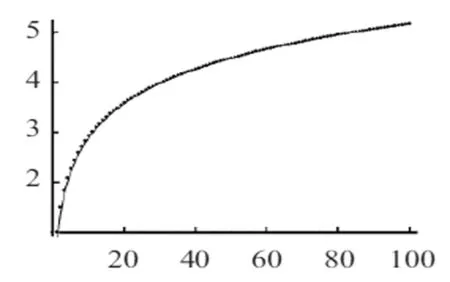
图3　调和级数与ln x　　　　之差图

通过对比发现，如图2,虽然两个图形没有重合，但具有随自变量增加越来越接近一个常数的特征.是否相差一个常数？我们选择n=1 000时的常数0.577 266来验证,我们将0.577 266+lnx图形和前n项调和级数的散点图放在一起比较.

q=Plot[Log[x]+0.577266,{x,1,100}]

Show[t,q]

图3中显示两个函数几乎重合，这个显示结果提示我们，极限

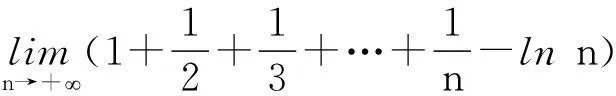
例4(应用实验)一艘游船载有1 000人，一名游客患了某种传染病，10h后有2人被传染发病.由于这种传染病没有早期症状，故传染患者不能被及时隔离.假设直升飞机将在50～60h将疫苗运到，试估算疫苗运到时患此传染病的人数[5].

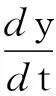
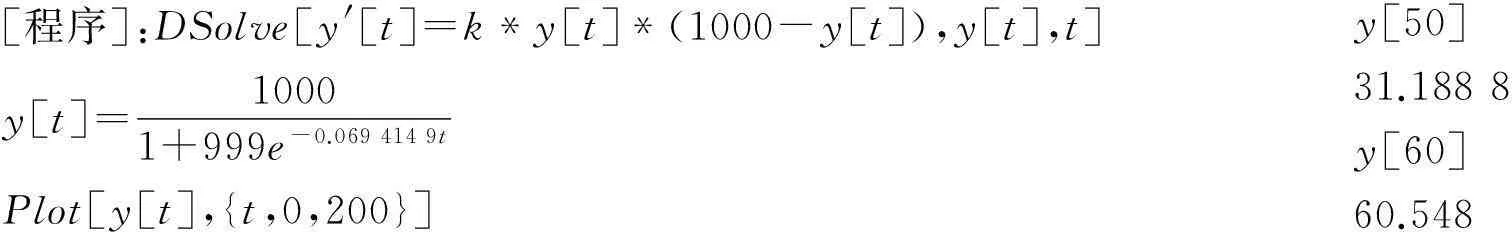
[程序]:DSolve[y'[t]=k*y[t]*(1000-y[t]),y[t],t]y[t]=10001+999e-0.0694149tPlot[y[t],{t,0,200}]y[50]31.1888y[60]60.548

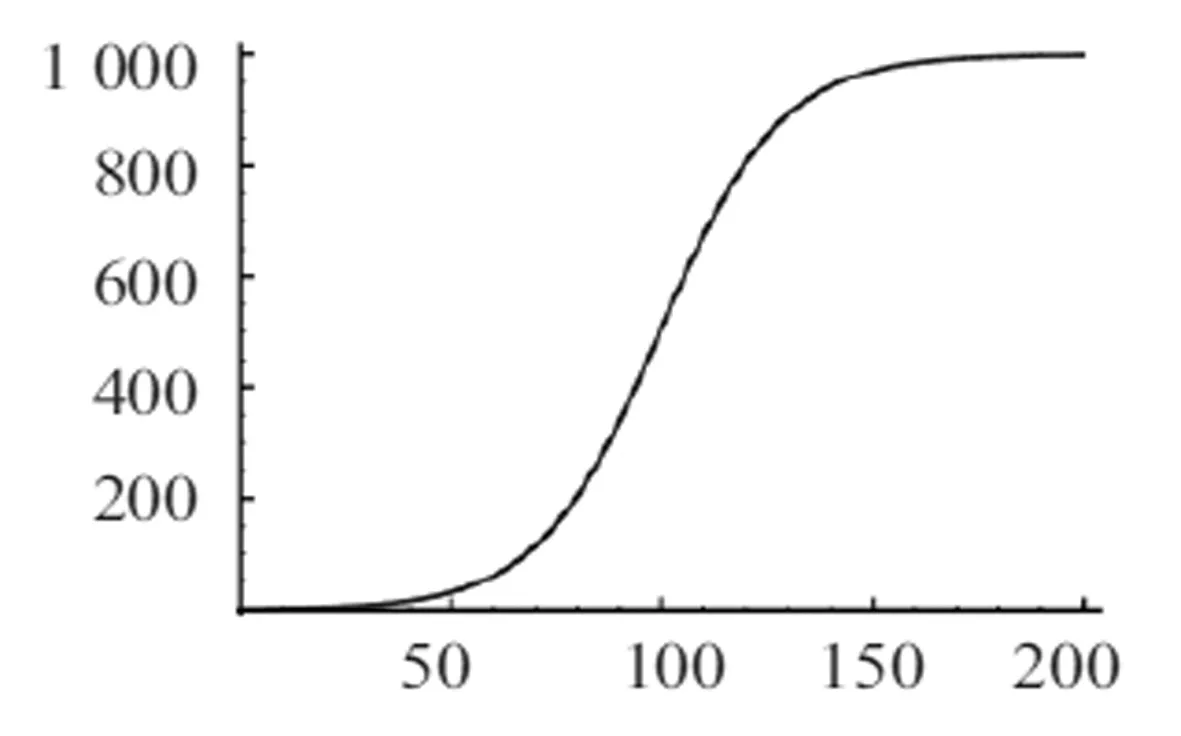
图4传染病模型

由以上数据发现在t=50h：患此传染病的人数约为32人；在t=60h：患此传染病的人数约为61人.从这些数据可以看到，从50h到60h之间，被传染的人数几乎翻倍，因此在传染病流行期间应该及时采取措施是很重要的.如果不采取措施，从图形可以看到，当t在50～150h之间传染最快，且当t趋于无穷大时，y(t)趋于1 000人，即导致全游艇人数都被传染.

在高等数学课程中开设数学实验教学的研究将会为广大数学教育工作者提供新的视角，数学实验教学是学生应用数学解决实际问题的最佳途径；是培养创新型、应用型和复合型人才的最佳载体.随着教育教学改革的深入发展，相信这门创新性的课程一定会在培养和造就各类专门人才中发挥更大的作用.数学实验引入高数教学其目的不仅仅使学生掌握必要的数学知识，更重要的是把学生从枯燥复杂的题目计算当中解放出来，把更多的精力投入到更多的思想方法和探索发现新知识当中去，从而提高学生应用数学的意识和创新能力，以适应新时期高素质人才的需要.

4高等数学教学中开展数学实验的措施

4.1保持高等数学知识体系结构完整性

在教学内容安排上，保持高等数学原有基础知识内容与结构体系完整性，将数学实验、数学建模思想融入高数教学，但不能喧宾夺主，在每章节根据内容增加数学实验内容，在相关内容学习时介绍Mathematica的符号运算功能、图像功能；每章安排不少于2课时上机实验，引导学生利用课余时间继续实验验证、探索并写出实验报告.

4.2做好课程设置及管理

在传统的强调逻辑性、严谨性的教学模式下，使得大部分学生认为“高数有用，但不知如何用”，大大降低了大学生感受和应用数学的能力，大学生的创新能力得不到培养.因此，需要增强课程的合理性，提高学生对高数的兴趣，看到高数的应用性，数学实验和数学建模融入高数教学中，在一定程度弥补传统教学中数学应用意识的不足.

随着改革的提出，多数高校也引入了数学实验，但实际操作过程中，数学实验和高数是分家的两个课程，出现一方面数学实验教师只管数学实验的软件操作部分，不管高数知识，甚至不了解高数知识；另一方面，高数教师只管高数理论知识的讲解，不懂将理论和实践结合运用.造成这种现状的原因，一方面是改革只是生搬硬套，没有站在实用的角度，教师没有积极改变以前的教学模式和及时更新、学习新知识的积极性.另一方面，教学大纲、课时安排等管理中缺乏正确的政策来支持，教师无法大胆尝试创新.因此课程设置及管理是关键.

4.3改进教学内容、方法

在教学过程将如何将数学实验引入课堂教学内容来培养学生的自主性、独立性、合作性和创新性，让学生的才智得到充分发挥，从而提高综合素质.需要教师改变传统模式，重新考虑制定教学计划、教学大纲、编写教案；组织课堂讨论、搜集编写综合实验案例、引导学生搜集查阅文献、指导建立数学模型方法步骤、指导实验与课题设计、批阅实验报告.其中合理的教学建模案例是重难点，教学案例要新颖、要体现数学建模的基本思想方法，又不能远离学生让学生失去兴趣，还要分类出不同应用背景的案例，因此也希望有关教育部门及学校提供基金项目支持，鼓励和加强数学建模与数学实验案例库和问题库的建设，确保数学实验、建模思想有成效的引入高数课堂教学.

4.4制作调查分析对比表

调查引入数学实验的试点班级和没引入数学实验的班级，制作调查对比表，从数学实验对高数学习的帮助情况；学习兴趣；提高计算机运用能力；解决实际问题能力；培养创新探究能力；课程比例合理性；考核方式科学性等主要方面调查对比，研究数学实验引入高数教学的成效并及时调整教学方式.

4.5制定科学的考核方式

数学实验的考核应重视实践的全过程，着重考核学生的创新思维能力和数学素养在实践过程中的体现.根据学生实验前的准备情况、实验过程的操作情况、实验报告的完成情况进行全面考核.学生成绩=高数知识成绩×30%+基础实验成绩×20%+综合实验建模成绩× 30%+建模论文× 20%.高数卷面考试成绩，采用传统考试模式，重点考察基本概念、定理性质、数学思想方法的理解；基础实验成绩和探索应用实验成绩，试题前半部分给出高数知识的计算题目，让学生独立上机利用所学数学软件完成计算，试题后半部分给出探索应用题目，学生独立上机完成探索、简单建模问题，并写出简单的上机实验报告；综合实验问题，给出生活实际问题，将学生3～5人成立若干建模小组，模拟数学建模比赛模式，学生分共完成搜集文献，建立模型，上机编程得出结论、完成建模论文.

培养创造性人才是教育的目标和努力方向，高等数学的理论和方法对培养学生的创新素质和后续课程的学习都有重要的作用.数学实验是用数学来解决实际问题的桥梁，因此作为数学教育工作者要重视将数学实验、数学建模思想和方法融入到数学教学中，使我们的数学教学对培养创新型人才起到重要作用.

参考文献：

[1] 刘志强,姚雪青.创新点燃中国经济新引擎[N].人民日报,2016-03-03

[2] 李岚. 高等数学教学改革研究进展[J].大学数学，2007,23(4):20-26.

[3] 王丽静,樊永艳,张 静.基于创新人才培养的大学数学课程体系改革[J] .沧州师范学院,2015,31(1)：16-119.

[4] 高洁,周玮. 在高等数学课程中开展数学实验教学的探索与研究[J].数学教育学报,2015,24(3):86-90.

[5] 王兵团,刘晓.数学实验基础[M].北京：清华大学出版社，北京交通大学出版社,2006:46-65.

收稿日期：2016-04-25

基金项目:国家自然科学基金资助项目(61370186)；2013年广东省高等院校学科建设专项资金项目(2013KJCX0140)

作者简介：辛冬梅，女，山东肥城人，广东第二师范学院数学系讲师.

中图分类号：G 642.0

文献标识码：A

文章编号：2095-3798(2016)03-0096-06

A Research on the Reform of College MathematicsCurriculumBasedontheCultivationofInnovativeTalents——TakingtheExperimentTeachingofHigherMathematicsasanExample

XINDong-mei1，YANZhi-lai2

(1.DepartmentofMathematics,GuangdongUniversityofEducation,Guangzhou,Guangdong, 510303,P.R.China;2.SchoolofEconomicsandManagement,GuangzhouUniversityofChineseMedicine,Guangzhou,Guangdong, 510000,P.R.China)

Abstract:Innovation is to lead the development of the first power. In the teaching of Higher Mathematics，introducing mathematics experiments, playing the role of basic experiment and exploration, the application and comprehensive modeling of the experimental, the reform of college mathematics courses, can cultivate innovative talents. Measures should be taken to develop the mathematical experiment in the teaching of Higher Mathematics: to maintain higher mathematics knowledge system, to complete the curriculum setting and management, to improve the teaching content, methods, survey analysis comparison table, to formulate scientific way of evaluation, to achieve knowledge innovation, to cultivate students′ comprehensive quality, innovation ability and innovative talents.

Key words:innovation talent; higher mathematics; mathematics experiment; curriculum reform