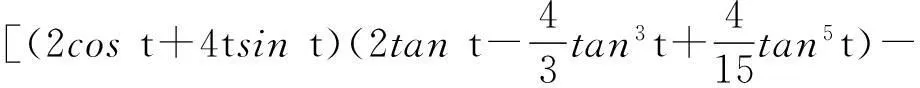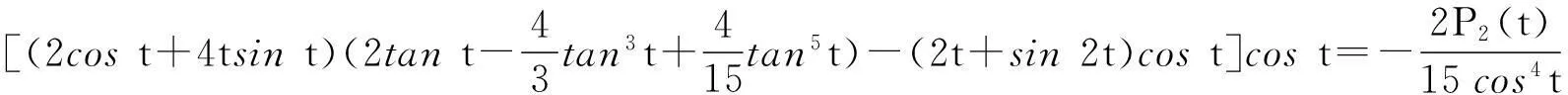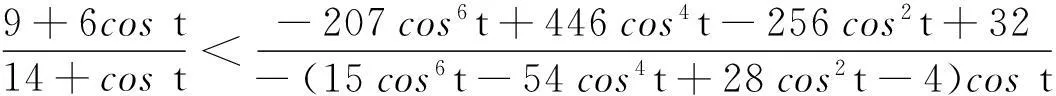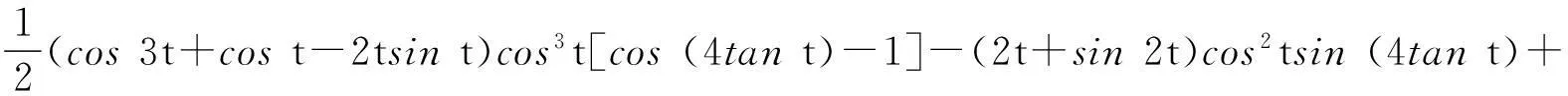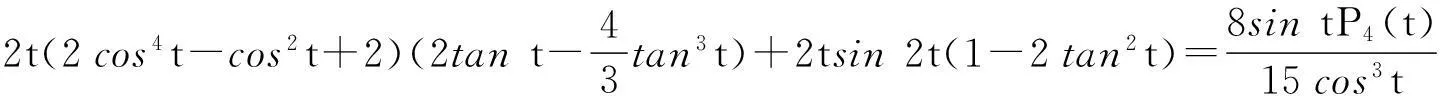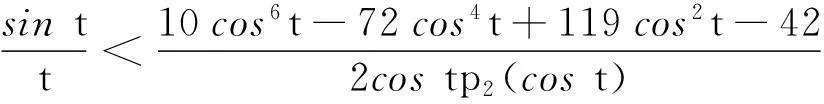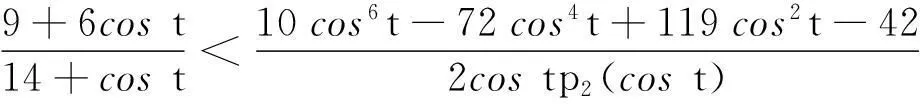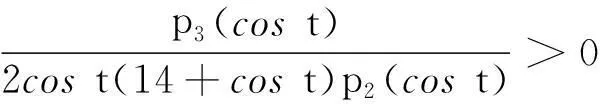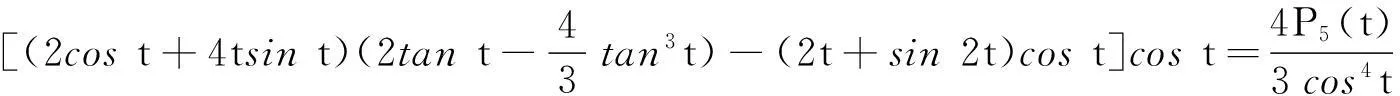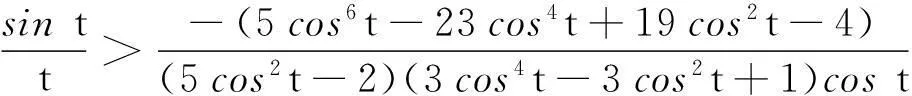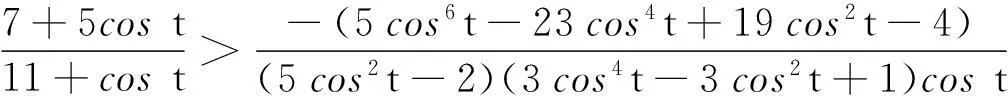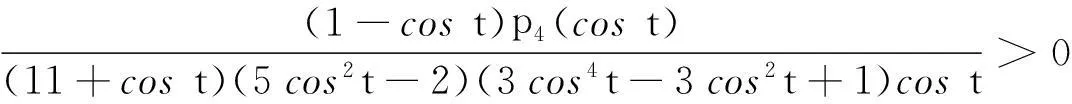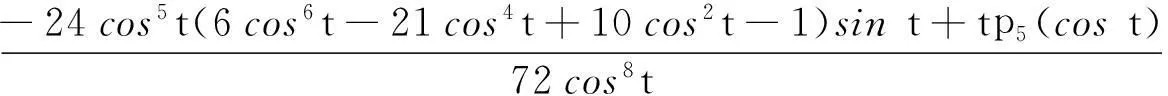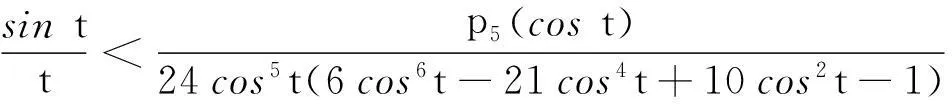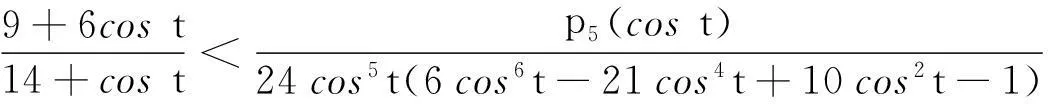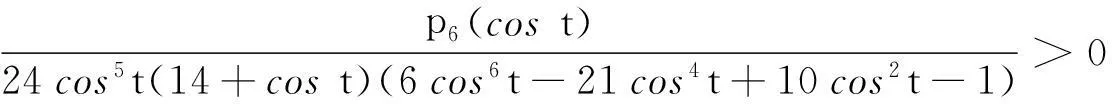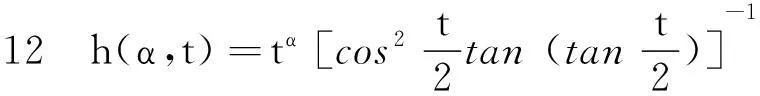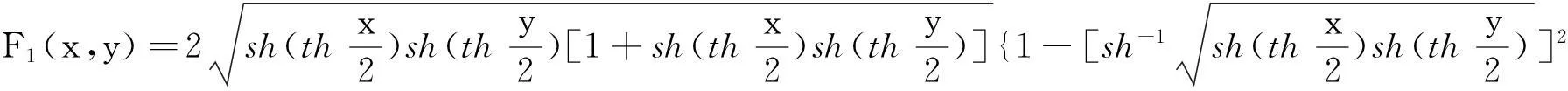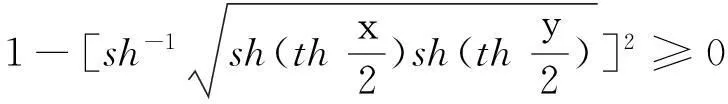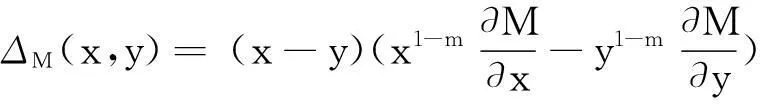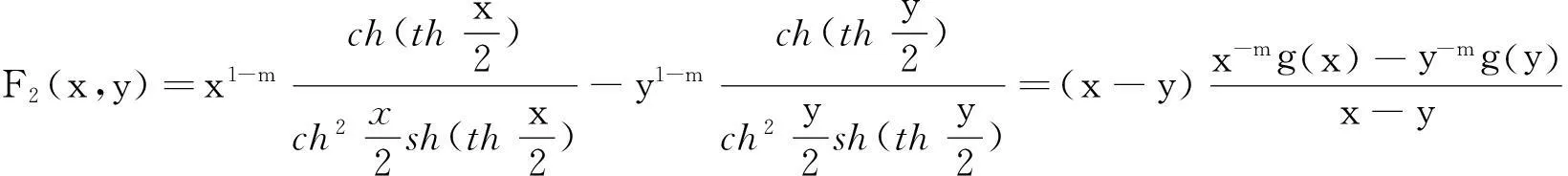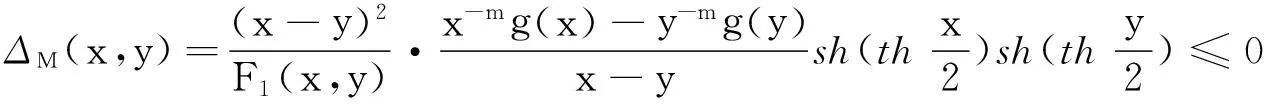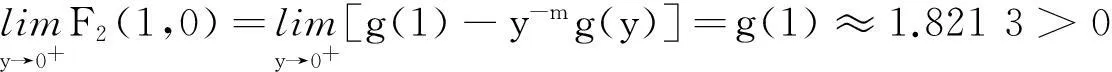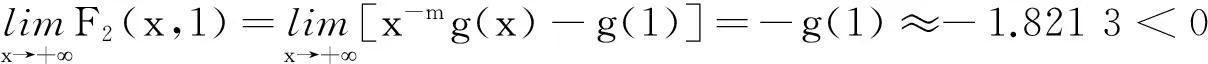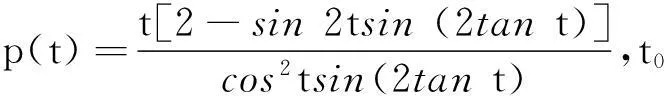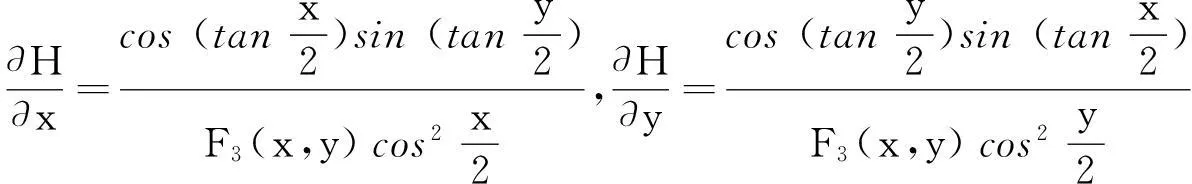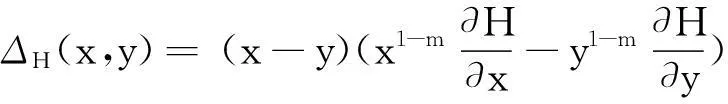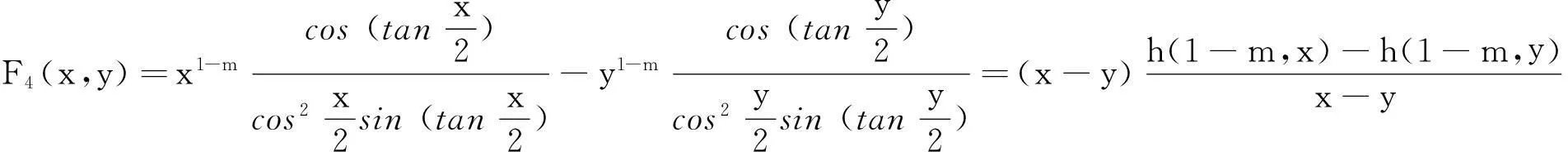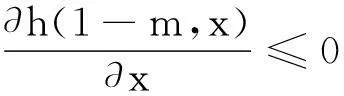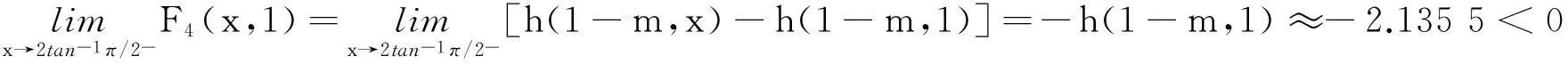关于两个“奇特”平均的Schur幂凸性

何　灯

(福清第三中学，福建 福清 350315)



关于两个“奇特”平均的Schur幂凸性

何灯

(福清第三中学，福建 福清 350315)

摘要:借助于maple数学软件和多项式判别系统,研究了涉及三角函数及双曲函数的两个“奇特”平均的Schur-幂凸性,给出了判定的充要条件.

关键词:Schur凸性；Schur-幂凸性；三角函数；双曲函数；多项式判别系统

0引言

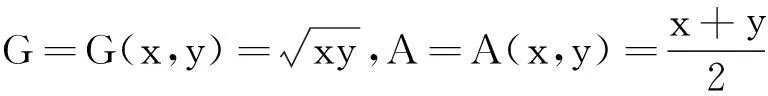
2003年,《美国数学月刊》11031问题定义了如下“奇特”平均并提出一个相关的不等式猜想:

问题11031设x,y>0,平均M(x,y)=lnN(x,y),其中

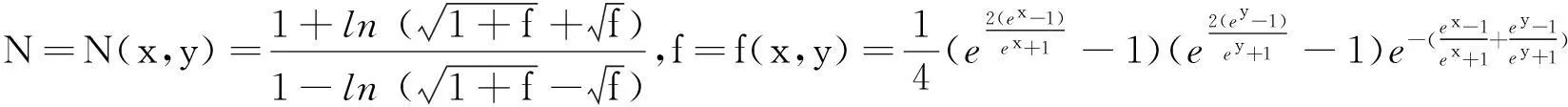
求证或否定M(x,y)≤G(x,y).

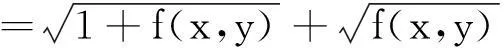
文献[3]研究了M(x,y)关于(x,y)在(0,+)2上的Schur-凸性和Schur-几何凸性,得到

定理1M(x,y)是(0,+)2上递增的Schur-凹函数和Schur-几何凹函数.

类似于M(x,y)的形式,本文定义如下三角函数及反三角函数复合的平均

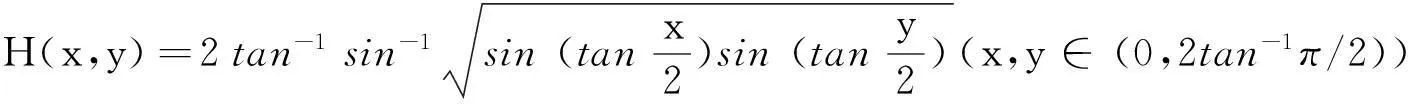
并借助于maple数学软件和多项式判别系统[4-5]，研究了M(x,y)及H(x,y)在各自定义域上更一般的性质—Schur-幂凸性[6-10].为此我们需要如下定义及引理.

1定义和引理

对于x=(x1,x2,…,xn)∈Rn,将x的分量递减重排后,记作x[1]≥x[2]≥…≥x[n].并用x≤y表示xi≤yi(i=1,…,n).

定义1[11]2设x,y∈Rn满足

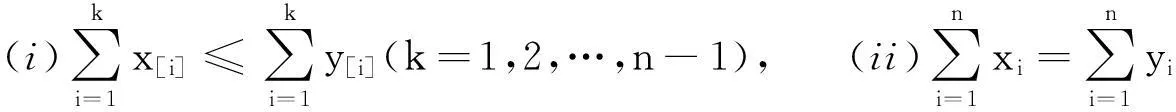
定义2[11]54设Ω⊂Rn, φ:Ω→R,

(i) 若在Ω上x≤y ⟹φ(x)≤φ(y),则称φ为Ω上的增函数;若-φ是Ω上的增函数,则称φ为Ω上的减函数.

(ii) 若在Ω上xy⟹φ(x)≤φ(y),则称φ为Ω上的Schur凸函数;若-φ是Ω上Schur凸函数,则称φ为Ω上Schur凹函数.

引理1[11]58设E(⊆Rn)是有内点的对称凸集,f:E→R为连续,且在E的内部intE可微,则f在E上为Schur-凸(凹)函数当且仅当f在E上对称,且对所有的x∈intE,都有

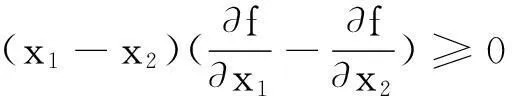
(1)

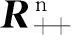
(lnx1,lnx2,…,lnxn)(lny1,lny2,…,lnyn)

时,都有f(x)≤f(y)成立,则称f是E上的Schur-几何凸函数;f为E上的Schur-几何凹函数,当且仅当-f为Schur-几何凸函数.

引理2[13]设E(⊆Rn)为有内点的对称集,{(lnx1,lnx2,…,lnxn)|x∈E}为凸集,f:E→R连续,且在intE内可微,则f为Schur-几何凸(凹)函数的充分必要条件是f在E上对称,且对所有的x∈intE,都有

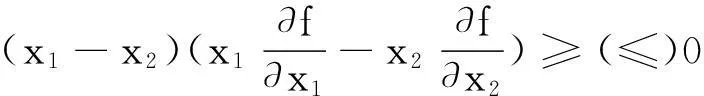
(2)

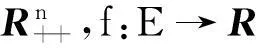
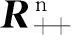
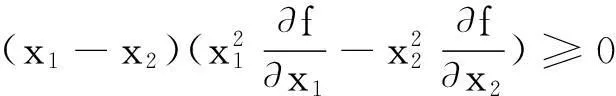
(3)

定义5[6-10](i)设f:R++→R是严格单调函数,Ω⊂Rn.若对于任何x,y∈Ω,总有f-1(αf(x)+βf(y))∈Ω,则称Ω是f-凸集,其中α,β∈[0,1]且α+β=1.

(ii) 设Ω⊂Rn,Ω内部非空.φ:Ω→R,对于任意x,y∈Ω,若f(x)f(y)时,有φ(x)≤φ(y),则称φ为Ω上的Schur-f凸函数;若-φ是Ω上Schur-f凸函数,则称φ为Ω上Schur-f凹函数.

由Schur-f凸函数的定义知,若g为单调递增(减),g(φ(x))有意义,则φ为Schur-f凸函数,当且仅当g°φ为Schur-f凸(凹)函数.

定义6[6-10]在定义5中若取

则称φ为Ω上的Schur-m阶幂凸函数;若-φ是Ω上Schur-m阶幂凸函数,则称φ为Ω上Schur-m阶幂凹函数.

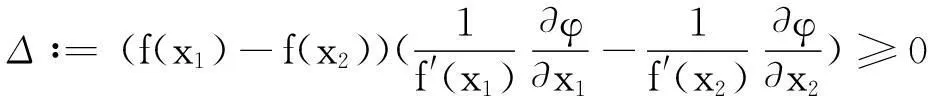
(4)

对于Schur-m阶幂凸函数,若m≠0,相应的Schur条件为

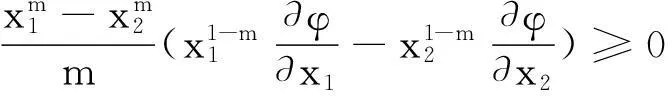
(5)

不难发现,式(4)综合了式(1)(2)(3)(5).

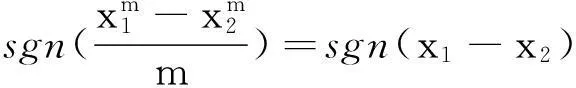
引理5[16]设a≤b,u(t)=tb+(1-t)a,v(t)=ta+(1-t)b,1/2≤t2≤t1≤1或0≤t1≤t2≤1/2,则

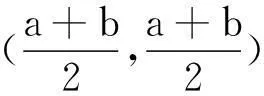
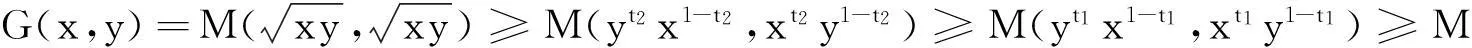
推论1 将问题11031作了隔离.

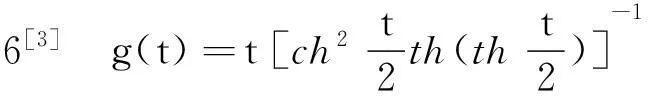
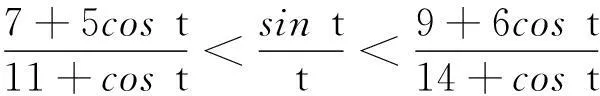
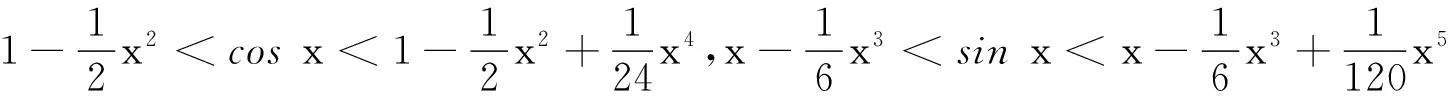
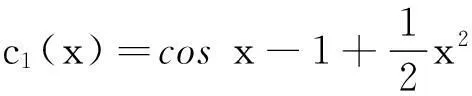
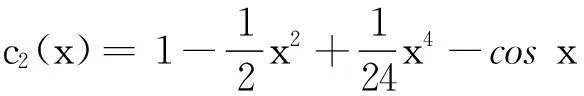
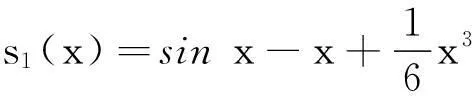
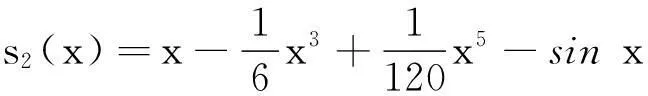
引理9[4]如果多项式H(x)的判别式序列的符号修订表的变号数是ν,那么H(x)的互异共轭虚根对的数目就是ν,而且,如果该符号修订表中非零元的个数是η,那么H(x)的互异实根的数目是η-2ν.

引理10(Ⅰ)设λ∈(0.921 0,1),则

p1(λ)=-45λ7-9λ6+1 602λ5+1 622λ4-1 584λ3-1 582λ2+222λ+224>0.

(Ⅱ)设λ∈(0.877 5,0.921 1),则

p2(λ)=15λ6+36λ4-52λ2+16>0,

p3(λ)=-180λ8-260λ7-292λ6-720λ5-384λ4+1 055λ3+1 474λ2-330λ-588>0.

(Ⅲ)设λ∈(0.786 4,0.877 6),则

p4(λ)=-75λ7-185λ6-135λ5+35λ4+233λ3+137λ2-62λ-44>0.

(Ⅳ)设λ∈(0.537 0,0.786 5),则

p5(λ)=-1 152λ10+407λ8+508λ6-222λ4+28λ2-1>0,

p6(λ)=-864λ12-2 448λ11-13 104λ10+4 943λ9+4 258λ8-1 652λ7+7 256λ6-

6λ5-3 108λ4+28λ3+392λ2-λ-14>0.

证明由于证明类似,此处仅给出p1(λ)>0的验证.利用引理9和文献[4]中给出的DISCR程序,可求p1(λ)的判别式序列的符号表和符号修订表均为[1,1,1,1,1,1,1],其变号数为0,则p1(λ)有0对互异的虚根,有7个互异实根,借助于maple数学软件可求这7个实根分别为-5.385 1…,-1.149 2…,-0.821 2…,-0.417 1…,0.413 4…,0.908 3…,6.250 9…,显然这7个实数根并未落在区间(0.921 0,1)上,从而p1(λ)在(0.921 0,1)上恒正或恒负,又p1(0.93)≈83.020>0,则当λ∈(0.921 0,1),p1(λ)>0.

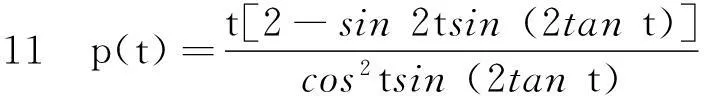
[(2cost+4tsint)sin(2tant)-(2t+sin2t)cost]cost.

下面将证明P1(t)在t∈(0,0.4]上取值恒为负,在t∈[0.4,0.5]上单调递增,在t∈[0.5,tan-1π/2)上取值恒为正.

(i)当t∈(0,0.4],可求

0.921 0

由引理8得

其中

P2(t)=(15cos6t-54cos4t+28cos2t-4)costsint+(-207cos6t+446cos4t-256cos2t+32)t,

注意到cost∈(0.921 0,1),则

15cos6t-54cos4t+28cos2t-4≤-39cos4t+28cos2t=

(-39cos2t+28)cos2t≤(-39cos20.4+28)cos2t≈-5.085 8cos2t<0,

从而欲证P2(t)>0,等价于证明

由引理7,只需证明

等价于证明

由引理10(I),上式成立,从而P2(t)>0,P1(t)<0.

(ii)当t∈[0.4,0.5],可求

0.877 5

P3(t)=-(cos3t+cost-2tsint)cos3tsin2(2tant)-(2t+sin2t)cos2tsin(4tant)+

2t(2cos4t-cos2t+2)sin(2tant)+2tsin2tcos(2tant),

注意到

(cos3t+cost-2tsint)′=(4cos3t-2cost-2tsint)′=-2cost(6sintcost+t)<0,

则

cos3t+cost-2tsint≥cos1.5+cos0.5-sin0.5≈0.468 9>0,

从而由引理8得

2t(2cos4t-cos2t+2)sin(2tant)+2tsin2tcos(2tant)≥

其中

P4(t)=-2costp2(cost)sint+(10cos6t-72cos4t+119cos2t-42)t,

由引理10(Ⅱ),欲证P4(t)>0,只需证明

由引理7,只需证明

等价于证明

(iii)当t∈[0.5,tan-1π/4],可求

0.786 4

0.546 3

0≤cos(2tant)≤cos(2tan0.5)<0.460 2,

由引理8得

其中

P5(t)=(5cos2t-2)(3cos4t-3cos2t+1)costsint+(5cos6t-23cos4t+19cos2t-4)t,

易证(5cos2t-2)(3cos4t-3cos2t+1)>0,则欲证P5(t)>0,只需证明

由引理7,只需证明

等价于证明

由引理10(Ⅲ),上式成立,则P1(t)>0.

(iv)当t∈[tan-1π/4,tan-1π/2),可求

0.537 0

π/4=tan(tan-1π/4)≤tant

由引理8得

P1(t)≥-4tcos(2tant)+[(2cost+4tsint)sin(2tant)-(2t+sin2t)cost]cost=

-4t[2cos2(tant)-1]+[2(2cost+4tsint)sin(tant)cos(tant)-(2t+sin2t)cost]cost≥

由引理10(Ⅳ)得tp5(cost)>0,则当6cos6t-21cos4t+10cos2t-1≤0,显然有P1(t)>0,当6cos6t-21cos4t+10cos2t-1>0,欲证P1(t)>0,只需证明

由引理7,只需证明

等价于证明

由引理10(Ⅳ),上式成立.

综合上述四类讨论,可得P1(t)在t∈(0,tan-1π/2)上存在唯一实根t0,且t0落在区间(0.4,0.5)上,借助于maple数学软件可求t0≈0.468 77.则当t∈(0,t0),P1(t)<0,p′(t)<0,p(t)单调递减,当t∈(t0,tan-1π/2),P1(t)>0,p′(t)>0,p(t)单调递增.从而p(t)≥p(t0).

证明作代换t=2x,则等价于证明q(α,x)=xα[cos2xtan(tanx)]-1关于x在(0,tan-1π/2)上单调递减,又

结合引理11得

综上,引理12得证.

2主要结果及证明

证明

其中

注意到

当m≥0,由引理6可得t-mg(t)在(0,+)上单调递减,则

当m<0,计算得

显然ΔM(x,y)在(0,+)2上符号不恒定,从而M(x,y)不是(0,+)2上Schur-m阶幂凹(凸)函数.

综上,定理2得证.

证明

其中

结合引理12得

从而当且仅当m≥1-p(t0)时,H(x,y)关于(x,y)在(0,2tan-1π/2)2上Schur-m阶幂凹.

对任意m∈R,计算得

显然不存在m<1-p(t0)使得对任意(x,y)∈(0,2tan-1π/2)2恒有ΔH(x,y)≥0,从而H(x,y)不是(0,2tan-1π/2)2上Schur-m阶幂凸函数.

综上,定理3得证.

令定理3中m=1可得

推论2H(x,y)为(0,2tan-1π/2)2上Schur-凹函数.

由推论2并结合定义2及引理5可得

推论3对于(x,y)∈(0,2tan-1π/2)2,x≤y,1/2≤t2≤t1≤1或0≤t1≤t2≤1/2,有

H(t1y+(1-t1)x,t1x+(1-t1)y)≥H(x,y).

参考文献：

[1] 张小明.几何凸函数[M],合肥:安徽大学出版社,2004:107-108,118-121.

[2] 李大矛,石焕南.一个二元平均值不等式猜想的新证明[J].数学的实践与认识,2006,36(4):278-283.

[3] 石焕南.受控理论与解析不等式[M].哈尔滨:哈尔滨工业大学出版社,2012:283-287.

[4] 杨路,张景中,侯晓荣.非线性代数方程组与定理机器证明[M].上海:上海科技教育出版社,1996:137-166.

[5] 杨路,夏壁灿.不等式机器证明与自动发现[M].北京:科学出版社,2008:33-46.

[6]YANGZhen-hang.SchurpowerconvexityofStolarskymeans[J].PublMathDebrecen, 2012,80(1-2):43-66.[7] 张小明.几个n元平均的积的Schur-p阶幂凸性[J].湖南理工学院学报,2011,24(2):1-6,13.

[8]YANGZhen-hang.SchurpowerconvexityofGinimeans[J].BullKoreanMath.Soc,2013,50(2):485-498.

[9]YANGZhen-hang.SchurpowerconvexityofDaróczymeans[J].MathInequalAppl,2013,16(3):751-762.[10] 邓勇平,吴善和,何灯.关于广义Muirhead平均的Schur幂凸性[J].数学的实践与认识,2014,44(5):255-268.[11] 王伯英.控制不等式基础[M].北京:北京师范大学出版社,1990.

[12] 张小明,续铁权.广义SCHUR-几何凸函数的定义及其应用[J].青岛职业技术学院学报,2005,18(4):60-63.[13] 张小明,褚玉明.解析不等式新论[M].哈尔滨:哈尔滨工业大学出版社,2009:93-94.

[14]GUANKai-zhong.Schur-convexityofthecompletesymmetricfunction[J].MathInequalAppl,2006,9:567-576.

[15]GUANKai-zhong.Somepropertiesofaclassofsymmetricfunctions[J].JMathAnalAppl,2007,336:70-80.

[16] 李大矛,顾春,石焕南.Heron平均幂型推广的Schur凸性[J].数学的实践与认识,2006,36(9):387-390.

[17] 李明,何灯.sinx/x的较强上下界估计及其应用[J].北京联合大学学报,2010,24(2):47-48.

收稿日期：2015-12-15

作者简介：何灯,男,福建福清人,福建省福清第三中学教师,全国不等式研究会成员.

中图分类号：O122.3

文献标识码：A

文章编号：2095-3798(2016)03-0030-09

The Schur Power Convexity for Two Special Mean

HE Deng

(Number 3 Middle School， Fuqing， Fujian， 350315， P.R.China)

Abstract:Based on the mathematical software-Maple and polynomial discrimination system, we study two special mean about trigonometric functions and hyperbolic functions.We give the necessary and sufficient conditions for the judgment.

Key words:Schur convexity; Schur power convexity; trigonometric functions; hyperbolic functions; polynomial discrimination system