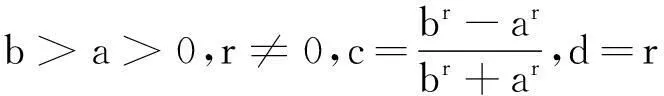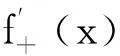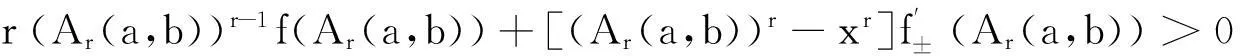与MH凸函数有关的积分不等式和单调函数

时统业，李照顺，夏　琦

(海军指挥学院 信息系， 江苏 南京 211800)



与MH凸函数有关的积分不等式和单调函数

时统业，李照顺，夏琦

(海军指挥学院 信息系， 江苏 南京 211800)

摘要:利用MH凸函数与凸函数的关系，证明了MH凸函数单侧导数的存在性和单调性，并通过不等式建立了MH凸函数与其单侧导数的联系．从MH凸函数的定义和基本性质出发，用普通数学分析的方法建立了若干MH凸函数的不等式，并证明了若干与MH凸函数有关的函数的单调性．

关键词:MH凸函数；积分不等式；单调性；单侧导数

0引言和引理

定义1[1]设f(x)在区间I上有定义，f(x)在I上称为凸(凹)函数，当且仅当：对任意x1，x2∈I，λ∈(0，1)，有

f(λx1+(1-λ)x2)≤(≥)λf(x1)+(1-λ)f(x2)．

定义2[2]设I(0,+∞)，f：I→(0,+∞)，若对任意x1，x2∈I和任意t∈[0，1]，存在r∈R，使得

(1)

则称f为I上的MH-凸函数；若不等式(1)中的不等号反向，则称f为I上的MH-凹函数．

当r=0时，MH-凸函数即GH-凸函数[3]．本文只考虑r≠0的情形．

引理1[2]设I=[a，b](0,+∞)，f：I→(0,+∞)，则f为I上的MH-凸(凹)函数的充要条件是为Ir={xr|x∈[a,b]}上的凹(凸)函数．

引理2[2]设I(0,+∞)，f：I→(0,+∞)，且二阶可导，则f(x)为I上的MH-凸(凹)函数的充要条件是x[2(f′(x))2-f(x)f″(x)]-(1-r)f(x)f′(x)≤(≥)0 (x∈I)．

引理3[4]设f(x)为区间I上的凸函数，则f(x)在开区间(a，b)I内处处存在左、右导数(从而处处连续)，且对x，y∈(a，b)，x

注1当f(x)为区间I上的凹函数时，也有相应结论，即引理3中的不等号反向．

引理4设f(x)为[a，b]上的凸(凹)函数，则对任意x∈[a，b]，y∈(a，b)，有

证明当x=y时结论显然成立.由凸(凹)函数的定义，对任意x∈[a，b]，y∈(a，b)，x≠y，t∈(0，1)，有f(tx+(1-t)y)≤(≥)tf(x)+(1-t)f(y)，由此得

(i) f在(a，b)内任意点处的单侧导数存在；

(ii) 当x，y∈(a，b)，x

(2)

(iii) 对任意x∈[a，b]，y∈(a，b)，有

(3)

证明只证明r>0情形，当r<0时同理可证．

也即对任意x∈(ar，br)有

(ii) 当x，y∈(ar，br)，x

由此证得式(2)成立．

(iii) 因g(x)是[ar，br]上的凹(凸)函数，故由引理3证得式(3)成立．

本文首先建立一些MH凸函数的积分不等式，所采用的思想方法来自文献[7]和[8]．然后建立一些与MH凸函数有关的四个单调函数，第一个来自于MH凸(凹)函数的Hermite-Hadamard不等式，第二个是在研究MH凸函数的变上限积分的凸性时产生的，第三个单调函数由MH凸函数的定义生成，第四个由引理5关于单侧导数的单调性得到．

1与MH凸函数有关的不等式

(4)

证明由MH凸函数的定义，对任意t∈[0，1]，有

(5)

当brf(b)≠arf(a)，且f(b)≠f(a)时，

当brf(b)=arf(a)时，

当f(b)=f(a)时，

(6)

证明由引理5，对任意x∈[a，b]，y∈(a，b)，得

(7)

(8)

式(7)、(8)乘以xr-1然后分别在[a，y]和[y，b]上对x积分，然后相加即得式(6)．

(9)

其中

证明因为对任意x∈[a，b]有

分别取x=a和x=b，得s∈(-1,1)．在推论1中取y=Ar(a,b)，则式(9)的左边不等式得证．

(10)

证明由引理5(iii)，对任意x∈[a，b]，有

(11)

同理可得

(12)

式(11)、(12)相加可得式(10)．

(13)

其中

s0∈(0,1)是方程1+cs=c(1-s2)[d+ln(1+s)-ln(1-s)]的唯一解．

证明在推论3中取y=Ar(a,b)，则式(13)的左边不等式得证．又由引理6，式(13)的右边不等式得证．

(14)

其中

证明由引理5(iii)，对任意x∈[a，b]，y∈(a，b)，有

(15)

(16)

将式(15)、(16)乘以p(x)然后分别在[a，y]和[y，b]上对x积分，然后相加得

(17)

在式(17)中取y=y0，则y0∈(a,b)，且

2与MH凸函数有关的单调函数

在(a，b)上单调增加(减少)．

证明对任意x∈(a，b)，有

其中

-xf(x)f″(x)≤(1-r)f(x)f′(x)-2x(f′(x))2，

于是有

v(x)≤-x2(f′(x))2+2p(1-r)xf(x)f′(x)+(p+r)(1-r)f2(x)=

在(a，b)单调增加(减少)．

证明设f为单调增加的MH凸函数.对任意x∈(a，b)，有

其中

由引理5及f的单调增加性有

又由MH凸函数定义有

证明对任意x∈(a，b)，有

因为x

参考文献：

[1] 裴礼文．数学分析中的典型问题与方法[M]．2版．北京：高等教育出版社，2006：268．

[2] 宋振云．MH-凸函数及其Jensen型不等式[J]．杭州师范大学学报(自然科学版)，2015，14(2)：156-160．

[3] 陈少元．GH-凸函数及其Jensen型不等式[J]．首都师范大学学报(自然科学版)，2013，34(5)：1-5．

[4] 刘三阳，李广民．数学分析十讲[M]．北京：科学出版社，2011:89．

[5] 杨军．用单侧导数判断函数的单调性[J]．四川师范学院学报(自然科学版)，2000，21(1)：108-109．

[6] 李丹衡，邓远北．函数的左、右导数的应用[J]．高等数学研究，1999，2(3)：26-28．

[7] 张小明，褚玉明．解析不等式新论[M]．哈尔滨：哈尔滨工业大学出版社，2009：139-148,180-184,198-200,208-212.

[8]DRAGOMIRSS，PEARCECEM．SelectedtopicsonHermite-Hadamardinequalitiesandapplications[EB/OL].[2015-10-12].http://rgmia.vu.edu.au/SSDragomirweb.html．

收稿日期：2015-11-16

作者简介：时统业，男, 河北张家口人，海军指挥学院信息系副教授.

中图分类号：O178

文献标识码：A

文章编号：2095-3798(2016)03-0023-07

Integral Inequalities and Monotone Functions Related to MH-Convex Functions

SHI Tong-ye， LI Zhao-shun， XIA Qi

(Department of Information， PLA Naval Command College， Nanjing， Jiangsu,211800， P.R.China)

Abstract:With the aid of relationship between MH-convex functions and convex functions，the existence and monotonicity of unilateral derivatives of MH-convex functions are proved，and the relation between MH-convex function and its unilateral derivative is established through inequalities. Starting from the definition and basic properties of MH-convex functions，integral inequalities for MH-convex functions are obtained by using mathematical analysis，and the monotonicities of several functions related to MH-convex functions are proved．

Key words:MH-convex function；integral inequality；monotonicity；unilateral derivative