不等式自动发现与判定程序agl2012典型应用9例

刘保乾

(西藏自治区组织编制信息管理中心，西藏 拉萨 850000)



不等式自动发现与判定程序agl2012典型应用9例

刘保乾

(西藏自治区组织编制信息管理中心，西藏 拉萨 850000)

摘要:收集了不等式自动发现与判定程序agl2012的9个应用实例.这些实例展现了agl2012程序的强大功能，为研究应用提供现成的模板和参考.总结了软件使用的策略和技巧，开启了相应的研究课题(一些课题内容是首次提出的，如乘积型不等式的局部对称式),精选了部分不等式自动发现新成果,提出了待解决的问题.

关键词:不等式自动发现；agl2012程序；问题

不等式自动发现与判定程序agl2012[1-3]自问世以来，经过几年的优化、补充和完善，尤其是通过消化吸收使用者反馈的意见，使软件日趋成熟.但如何进一步提高发现不等式的质量和效率，开发软件潜能，仍存在不少挑战和问题.本文收集了软件使用过程中积累的9个应用实例,总结了软件使用的策略和技巧，开启了相应的研究课题，提出了待解决的问题.

以下约定ΔABC三边为a,b,c，中线为ma,mb,mc，高为ha,hb,hc，角平分线为wa,wb,wc，旁切圆半径为ra,rb,rc，内切圆半径为r，外接圆半径为R，半周为s.用∑表示循环和.

1对称类型求和公式

文献[4-6]中建立的对称类型求和公式(如完全对称求和dc，轮换对称求和sgm，schur型求和schur，平方类求和pf，生成运算类求和ston等)，是一类十分重要的求和类型，在多项式不等式研究中有许多应用.

1.1研究有关对称类型多项式线性空间的维数和基

这方面的应用请参阅文献[5]和文献[6]等.

1.2给出有关对称类型的具体表达式

由于3元多项式变元较少，要写出某种对称类型的表达式，用肉眼观察和手工书写就可以完成.但对4元以上的多项式，虽然理论上写出表达式通式很容易，但要具体把表达式书写出来就比较困难，而给出具体的表达式，是机器证明研究的关键技术，也是平时研究和推广不等式时经常遇到的难题.

例1文献[7]的第一作者在最初研究多元schur型多项式时，曾遇到书写出5元schur型多项式(分拆基)的困难，当时在中国不等式研究小组网站论坛向本文作者求助.事实上用schur型对称类型求和公式schur或生成运算型求和公式ston很容易得到(共30项).如由命令

>schur4(x1*(x1-x2)*(x1-x3));

可输出表达式

x1(x1-x2)(x1-x3)+x3(x3-x2)(x3-x5)+x5(x5-x4)(x5-x2)+x1(x1-x5)(x1-x3)+

x3(x3-x5)(x3-x1)+x1(x1-x5)(x1-x4)+x5(x5-x2)(x5-x1)+x1(x1-x2)(x1-x5)+

x4(x4-x3)(x4-x5)+x5(x5-x4)(x5-x3)+x5(x5-x3)(x5-x2)+x3(x3-x4)(x3-x5)+

x5(x5-x1)(x5-x4)+x2(x2-x1)(x2-x5)+x4(x4-x2)(x4-x5)+x2(x2-x3)(x2-x5)+

x2(x2-x4)(x2-x5)+x4(x4-x5)(x4-x1)+x4(x4-x1)(x4-x2)+x3(x3-x1)(x3-x2)+

x1(x1-x3)(x1-x4)+x1(x1-x2)(x1-x4)+x4(x4-x1)(x4-x3)+x2(x2-x3)(x2-x1)+

x2(x2-x3)(x2-x4)+x4(x4-x2)(x4-x3)+x2(x2-x4)(x2-x1)+x3(x3-x4)(x3-x2)+

x3(x3-x4)(x3-x1)+x5(x5-x3)(x5-x1).

例2伊朗96年数学竞赛曾有题目：设x,y,z>0，证明

(1)

如何把不等式(1)向多元进行推广一直是人们关注的问题.事实上，如果关注国外数学论坛http://artofproblemsolving.com就可以看到，有关推广和加强不等式(1)的贴子不时会出现，且成为热贴，但鲜有实质性推广者，根本原因是写不出多元中相应的表达式是什么？如果采用对称类型求和公式很快就可以发现推广式.

观察(1)的形式，适合平方型对称规律，现采用平方型求和公式pf.在不等式自动发现与判定程序agl2012环境下，键入命令：

>bd∶=pf4(x1*x2)*pf4(1/(x1+x2));

>bd-tocsn(bd);

(2)

用差分代换法[8]易证不等式(2)成立.

1.3过滤对称性重复数据

在对不等式自动发现结果进行分析时，会遇到类似于x3+y3+z3-x2y-y2z-z2x≥0,x3+y3+z3-xy2-yz2-zx2≥0的结果，这两个不等式本质上是一样的，需要过滤掉一个，文献[9]中gldccf函数就是利用对称类型求和公式设计的.

1.4构造配平方和数据

基于求线性方程组正数解程序lpsolve[10]的配平方和算法，本质上是一种验证算法，需要预先构造出分拆项[11]数据.对一个给定的半正定多项式，如果构造的配方数据没有覆盖到这个多项式所具有的配方形式，则配方可能会失败.尽量地构造大范围的数据，其实是这种配平方算法的无奈之举，也是这种算法的短处.另一方面，如果给出的配方数据量过大，则会因出现较多的方程而超出lpsolve的承解范围.在构造配平方和数据时，构造出新的数据形式是很重要的.而对称类型求和公式可以对此发挥独特的作用.

文献[12]定义了n元-t元对称类型.对于3元，有3元-2元对称求和公式

S3_2={f(x,y,z)+f(x,z,y),f(x,y,z)+f(z,y,x),f(x,y,z)+f(y,x,z)}

(3)

4元-3元对称求和公式比较复杂，如果用手工书写出来不仅麻烦而且还容易出错.为了得到4元-3元或更多元的局部对称求和公式，可用程序自动生成，命令如下：

>f(t, x, y, z);

>subs(x=x1, y=x2, z=x3, dc3(%));

>k*%;

>(1/6)*dc4(%);

>op(%);

>ld ∶={op(subs(k=1, [%]))};

>temp ∶={}; for i to 4 do ls ∶=0; lv ∶=op(ld[i]); print(111, lv);

for j to nops([lv]) do ls ∶=ls+subs(t=op(′minus′(′minus′({x1, x2, x3, x4}, {op(lv[j])}), {t})), lv[j]) end do; temp ∶=′union′(temp, {ls}) end do;

执行上述命令后，得到4元-3元对称求和公式

S4_3=f(x1,x3,x2,x4)+f(x1,x2,x4,x3)+f(x1,x4,x3,x2)+f(x1,x4,x2,x3)+

f(x1,x3,x4,x2)+f(x1,x2,x3,x4),f(x2,x1,x4,x3)+f(x2,x4,x3,x1)+

f(x2,x3,x1,x4)+f(x2,x3,x4,x1)+f(x2,x1,x3,x4)+f(x2,x4,x1,x3),f(x3,x1,x4,x2)+

f(x3,x4,x2,x1)+f(x3,x2,x1,x4)+f(x3,x2,x4,x1)+f(x3,x1,x2,x4)+f(x3,x4,x1,x2),

f(x4,x1,x2,x3)+f(x4,x2,x3,x1)+f(x4,x3,x1,x2)+f(x4,x3,x2,x1)+

f(x4,x1,x3,x2)+f(x4,x2,x1,x3).

(4)

S4_2以至更多元的对称类型求和公式，限于篇幅，本文暂不讨论.

有了这些对称求和公式，就可以编写相应的求和程序，对3元-2元对称类型，求和程序为esgm.如键入命令esgm(x*(x+y)^2)，得

{x(x+y)2+x(z+x)2,x(x+y)2+y(x+y)2,x(x+y)2+z(y+z)2}.

调用esgm就可以编写与3元局部对称类型有关的配平方程序，如命令fcxtsfjyc7.

例3笔者曾想得到3元非齐次不等式f=∑(1+xy)(z2+xy)-∑x(x+y)(y+z)≥0的配平方和，但一直得不到结果.但用命令fcxtsfjyc7易得f=(1/2)∑(yz+xy-y-z)2.

1.5构造不等式自动发现数据

对于agl2012程序来说，数据类型的构造形式决定自动发现结果的形式，所以构造优美工整的数据形式是十分重要的.利用上述esgm函数可以十分方便地构造局部对称数据，这些局部对称数据与完全对数的数据进行比较，就可以产生新颖的混合型不等式结果.

例4键入命令：

>d0 ∶=glerdcyz(qjcs(glxs(toesgm(toesgm(dssj(3)))), 2));#调用了esgm函数#

>d1 ∶=tysjsgm(6);#构造完全对称型数据#

>zjbj_otfqdcs(d1, d0, 0, 0, 1, 1, 1, 1);#d1和d0中的数据进行比较，结果存入jg中#

>glcj(glag(gldccf(jg)));#对结果进行初步过滤，取掉重复和平凡的#

执行上述命令后可得到199个优美的3元多项式不等式结果，如有不等式

(y+z)2(x2+yz)2≥(16/9)xyz∑x∑yz,∑xy5≥(3/4)(y+z)(x2+yz)xyz.

类似，易得4元不等式

(c+a)(b+d)(a2+c2+b2+d2)≥(16/9)d(a+b+c)(ab+bc+ac),

a4+c4+b4+d4≥(4/9)d(a+b+c)(a2+b2+c2).

如果没有对称类型求和公式，这类不等式是不容易被发现的.

2建立庞大的数据储备，以便随时查询调用

用agl2012程序发现不等式，一个基础条件是要构造数据.构造的数据愈丰富，输出的结果就愈多.如果把每次研究生成的数据按编号储备起来，形成海量数据库，这为今后的研究提供了极大的便利.这样每次只要输入感兴趣的目标表达式即可得到想要的结果.

>sjxmb0cfk (sqrt(cos(B)+cos(C)),1,10);#第1个参数1表示把发现的结果实时显示#

执行上述命令后，得到一个结果集，对这个结果集进行过滤，就会得到需要的结果.如

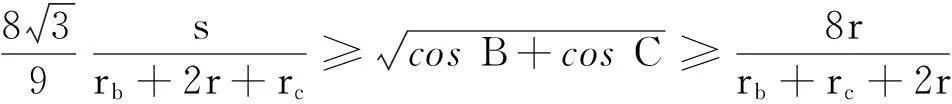
用类似的方法还可得优美不等式ma(4ra+rb+rc)≥2s2,等号成立当且仅当b=c或2a2+ab-3b2+ac+2bc-3c2=0.

ka(rb+rc)≥(1/2)(b+c-a)(a+b+c)等号成立当且仅当b=c或a2-c2-b2=0.

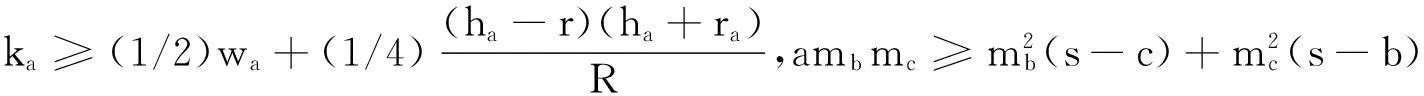
3不等式结果的选取

面对成千上万的不等式发现结果，到底哪些更有意义一些呢？这是不等式自动发现过程中经常要面对的一个问题.为此，agl2012程序设计了若干过滤器，这些过滤器的主要目的就是对输出结果进行选择.下面再介绍两种选择方法，即平方选择和最简集选择.

3.1平方选择

所谓平方选择，就是用配平方和命令对输出的结果进行选择，如果不能配出者，则保留；同时对能够配出平方者，选择简洁优美的留下来.这两部分保留下来的结果，就是平方选择的结果，即从配平方的角度，把输出结果中有价值的不等式挑选出来.

平方选择程序的算法可从两方面入手：一是考察配平方和结果中的项数，如果项数较少，如刚好是3项，则认为是简洁的；二是从结果表达式字符长度的数值来考虑，如果字符的长度比较小的话，则认为是比较简单的.由此可以设计出平方选择程序.

例6试建立3元6次多项式不等式，并按平方选择输出比较有价值的结果.

解键入命令：

>df∶=tysjsgm(6);#产生6次对称或轮换对称多项式，并置入变量df中#

>zjbj_otfqdcs(df,df,0,0,1,1,1,1,1);#对df中的数据进行比较，比较结果置入变量jg中#

>dd∶=gldccf(glcj(glag(jg)));#对jg中的结果进行初步过滤，包括a-g平凡过滤，积性过滤，以及对称性重复过滤#

>bf∶=gldj(dd);#进行等价性过滤，经以上过滤后，bf中还有710个多项式#

>azkc(bf, 6, 1, 20, 2)；#用配平方命令对bf进行选择，配出来的结果在tte变量中,没有配出来的多项式在temp变量中#

注意azkc命令的格式是azkc(ex,n,t,cd,dx) ，其中ex是欲配方的多项式集，n是分拆项中基本项的次数，t是对数据取差运算的重数，cd是分拆项的字符长度数值，dx是形如(xy+yz-tzx)2的附加项[13]中t的取值上限.一般开始选择时参数的值取的比较小，目的是为了构造较小的分拆项集参与平方分拆，以快速排除容易配平方者，大幅度缩小搜索范围.

>pfgl(tte);#挑选比较优美的配平方式#

这样可得到一批选择结果，如有配平方式

(xy+xz+yz)(x2y2+y2z2+x2z2)-3xyz(xy2+yz2+zx2)=∑(y-z)2zx3.

继续选择.键入命令:

>bf∶=temp;#把还没有配出来的多项式备份到变量bf#

>azkc(bf, 6, 1, 70, 6)；#开始对bf中的多项式进行平方选择，注意此时参数开始增加#

>pfgl(tte);#挑选比较优美的配平方式#

如有配平方式

(xy+xz+yz)(xy3+yz3+zx3)-(x+y+z)(x2+y2+z2)xyz=(1/2)∑(yz-x2)2z2.

>bv∶=temp;#bv中还有49个未配出者#

>azkc(bv, 6, 2, 70, 6);#这里设置的参数构造的分拆项集中的数据已经达到911个，此时配方速度明显变慢#

本轮配方后，简洁的配平方结果不多.temp变量中还剩余11个没有配出.

>azkcall(temp, 6, 1, 70, 6);#用新的命令对剩余的多项式进行平方选择#

经上述选择后，还有4个多项式没有配出来.最后用命令afcxtsfj(temp, 4, 2, 5, 7, 50)继续配方，结果配出来了3个，如

(y+z)(z+x)(x+y)(x3+y3+z3)-(8/9)(x+y+z)(x2+y2+z2)(xy2+yz2+zx2)=

(1/9)∑(2y-3x+z)2x2y2+(1/9)∑(2z-x-y)2z3x+(1/12)∑(z2-x2-2yz+2xz)2yz+(1/54)∑(3x2-2y2-2xz+z2)2yz+(1/108)∑(3x2-2y2-2xy+z2)2yz+(1/9)∑(2y2-3xz-yz+2xy)2yz.

(5)

剩下最后一个没有配出平方的不等式是

(xy2+yz2+zx2)(x2y+y2z+z2x)≥(x+y+z)(x2+y2+z2)xyz.

(6)

可以说，(6)是一个具有挑战性且又很优美的不等式问题.

由例6的解题过程可以看出，平方选择作为一种选择方式和标准，有其独特的意义：一方面可以筛选出简洁优美的配平方式；另一方面，对“还没有配出平方者”作为问题提出，能够增加问题的难度和吸引力.当然，对一些已经配出来的但形式复杂的配平方结果，如(5)式，仍可以作为问题提出来，那就是如何简化它的配方形式，或者给出其他方法的证明.

3.2最简集选择

由文献[14]知，一个集合Q的最简集Z1，其实就是这个集合的最佳不等式集.将Z1从Q中取出，得到集合Q1，求Q1的最简集Z2，Z2其实就是集合Q的次佳不等式集.如此做下去，就可以对集合Q中所有不等式进行排队.3元不等式集的排队命令是jqbest.

例7用jqbest命令对例6中bf变量中的710个不等式进行排队，可由强到弱得到若干不等式分组，第1组中的部分不等式是

这样由强到弱把不等式结果进行排序是有意义的，即使把不等式自动发现命令作为出题工具也应如此.因为从教学角度看，不同学习阶段、不同层次的学生需要不同强度的题目，这样的分组排序无疑使出题者心里更有数，针对性也更强.

4乘积型不等式的局部对称形式

所谓乘积型不等式，是指不等式的一边是循环积，另一边是对称式，即形如f(x,y,z)f(y,z,x)f(z,x,y)≥(≤)g(x,y,z)的不等式，其中g(x,y,z)必须是对称式或常数.如不等式8cosAcosBcosC≤1就是三角形中的乘积型不等式.不等式9(x+y)(y+z)(z+x)≥8(x+y+z)(xy+xz+yz)也可以看作是乘积型不等式.

如果对一个非对称的不等式两边取循环积，得到一个对称不等式，则这个非对称的不等式为这个对称不等式的乘积型局部对称不等式.

解键入命令：

>vv ∶=jxjbdc(′union′(qhcs(yc, 1), qhcs(lc, 1)));

>bv ∶=gldccftg(qjcss(bc3g({sin((1/2)*A)}), 3));

(或 bv ∶=gldccftg(qjcss(bc3g({cos((1/2)*A)}), 3)));

>bbv ∶=′minus′(bv, gldc3(bv));

>zjbj_otfqdcs(bbv, vv, 0, 1, 1, 1, 2);

易得

有些不等式表面上看不是乘积型不等式，但可以通过恒等变形化为乘积型不等式，从而得到其乘积型局部对称不等式.

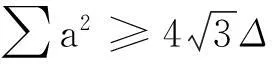
是否每一个乘积型不等式都存在相应的乘积型局部对称不等式？这个问题值得探讨。

5利用特殊取等号条件验证最佳值

在用agl2012程序研究不等式时常常需要确定最佳值或最佳系数，而优秀机器证明软件Bottema在确定最佳值时有独特优势.但对一些不等式，用Bottema软件确定最佳值时可能会出现时间过长，甚至不可能求解，在此情况下可以利用特殊取等号条件对不等式进行减元，以提高运算速度，从而改善Bottema软件性能.

5.1对称不等式的最佳值

经过研究发现，不少对称的不等式在取得最佳值时，等号成立的条件中往往有多个变元相等.那么反过来，在令一些变元相等时也可能会求得最佳值，这样就可以尝试性地解决一些难度甚大的问题.

对于3元对称不等式，在用Bottema求最佳值时，可令其中的两个变量相等；4元时可令3个变元相等.等求出最佳值后再用Bottema进行验证.

例10a,b,c,d>0，求最小k，成立不等式

解键入命令：

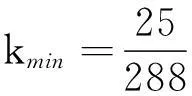
(7)

网友arqady已证明不等式(7)成立(http://artofproblemsolving.com/community/c6t243f6h1217059_xyzgt0prove_that).

类似可发现三角形中的最佳不等式

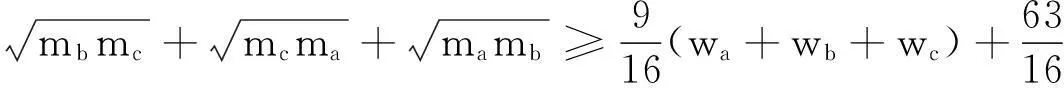
(8)

由于不等式(8)两边都含有根式型几何量，Bottema软件对(8)式难以进行判定，(8)的局部对称不等式也不易求得.由于还没有软件能够判定(8)式，故探讨(8) 式的解答很有意义.

5.2轮换对称不等式的最佳值

对轮换对称不等式，可令一个变量为零求最佳值.

解由命令sgm(ma/(a+b)) >=k; xmax(subs(x=0, aptoxp(%)), [], k)容易得到不等式

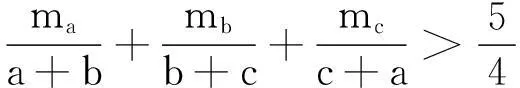
(9)

又用Bottema软件判定(9)式成立，从而得到最佳不等式(9).

注意：如果直接用Bottema的cmax命令，无法求解例10和例11中的问题，由此可见这里介绍的尝试性方法是有实际意义的，且具有某种不可替代的优点.

6三角形中的倍角不等式

在Maple系统中，expand命令可以将倍角三角函数展开，这个功能为自动发现倍角三角形不等式带来了极大的便利.了解到这一点，在agl2012环境下，许多优美且很强的倍角三角形不等式被源源不断地发掘出来.

例12在ΔABC中，容易发现优美倍角三角形不等式

cos 3A+cos 3B+cos 3C+8(cosA+cosB+cosC)≥9,

1≥cos 3Bcos 3C+cos 3Acos 3C+cos 3Acos 3B+2cos 3Acos 3Bcos 3C.

网友arqady已给出证明.

经验证有不等式

g(t)≥0(t=1,5,7,11,13).

(10)

不等式(10)值得研究，这不仅因为它优美的形式，而且当t>1时，不等式(10)对应的g(t)代数化后总是差分代换非平凡的，用其他方法证明难度也很大.另外，当t取奇素数时(10)好像成立？

7取补后成立的轮换对称不等式

如果两个同次的轮换对称多项式之和恰好是一个对称式，则称这两个轮换对称式是互补的.一个轮换对称式如果用f(x,y,z)表示，则它的补式必是f(x,z,y).

笔者在论坛http://artofproblemsolving.com上经常看到这样一类不等式：虽然轮换对称不等式f(x,y,z)≥0不成立，但f(x,y,z)+f(x,z,y)≥0成立.利用程序可以将此类不等式找出来(由于算法很简单，这里不作讨论).

例14键入命令 dd ∶=tysjsgm(5)，lhbclbua(dd, dd)， gldj3(glag(glcj(gldccf(ls))))，则输出8个优美的多项式不等式，如

(x+y+z)(x2y2+y2z2+x2z2)≥(1/2)∑yz∑yz(y+z),

x2y2(x+y)+y2z2(y+z)+z2x2(z+x)≥2(x2+y2+z2)xyz.

对于4元不等式，如何求补才能由轮换对称式得到完全对称式?此时可以考虑相应的对称类型求和公式.

例15有4元不等式(3/2)(ac+bd)(a2+c2+b2+d2)≥(bc+ad)(ab+cd)+(bc+ad)(ac+bd)+(ac+bd)(ab+cd).

(11)

不等式(11)十分优美.

8扩展Si类不等式

文献[13]提出了扩展Si类多项式.最近，笔者借助于Bottema软件发现了若干3元非平凡扩展Si类多项式，如

66(x+y+z)2(x2+y2+z2)-216(x+y+z)(x3+y3+z3)-31(x+y+z)4+

216(x+y+z)(xy2+yz2+zx2)+243(x4+y4+z4)≥0,

笔者把不等式(12)等发到http://artofproblemsolving.com论坛后，网友Nguyenhuyen_AG和文献[10]作者分别对其进行了解答，得到(12)的两种配方结果

∑(31x2-31y2-36xy+68yz-32zx)2≥0,∑(x-2y+z)2(11x+2y-7z)2≥0.

这两种配方结果实际上给出了扩展Si类不等式的2种不同构型.通过这些构型就可以编写发现扩展Si类不等式程序.现采用第2个配方式所具备的构型.其基本思路是：设扩展Si类多项式f(x,y,z)可表示为

f(x,y,z)=g(x,y,z)2+g(y,z,x)2+g(z,x,y)2.

则令g(x,y,z)=0,g(y,z,x)=0,g(z,x,y)=0，并解这个方程组.如果这个方程组有不相等的正数解，则f(x,y,z)≥0就是扩展Si类不等式.如对3元4次情形，可取

g(x,y,z)=(k1x+k2y-(k1+k2)z)(k3x+k4y+k5z),

(13)

以系数ki为循环变量建立方程组，逐次验证从而得到具体算法，由此可编写扩展Si类不等式验证程序.

例16键入命令equaons4c(-2,2)，可输出12个3元4次扩展Si类不等式，如有

(14)

如果将(13)式改为

g(x,y,z)=(k1x+k2y-(k1+k2)z)2(k3x+k4y+k5z)2(k6x+k7y+k8z),

(15)

则可得到验证3元5次扩展Si类不等式的程序equaons4c，用这个程序可发现形如

(16)

的众多3元5次扩展Si类不等式.可以看出，(16)式已不像(14)式那样是平凡非负的，因而很有意义.试给出不等式(16)的证明.另外，有如下对称的3元4次扩展Si类不等式：

扩展Si类不等式因其特殊的取等号条件，是一类很强的不等式，人们已经认知的此类不等式还不太多，但现在可以成批产生了.限于篇幅，4元扩展Si类不等式的讨论此略.

9用公式建立局部对称不等式

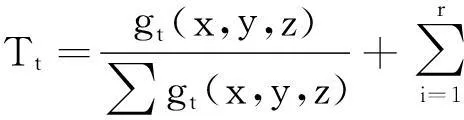
对于条件不等式，如约束条件为xyz+xy+yz+zx=4的不等式，2次的特征数据公式可表示为

因为由条件知xyz,xy,yz,zx也是不等式的特征数据.

特征数据公式的次数越高，则搜索空间越大，得到局部对称不等式的可能性就越大.但代价也是很高的.实际验证表明，当循环变量个数超过8时，搜索一遍的时间明显延长，如果再增加系数变化范围，那将是不可接受的代价.为此可尝试借助三角形解决这个问题.

例17 Vasc的一个著名不等式是(http://artofproblemsolving.com/community/c6t243f6h1215102_i_get_it21)

(17)

解对于不等式(17)，将特征数据公式取为T1,T2和T3，经验证均没有得到解.为此可将(17)等价地变为三角形不等式(可令x=s-a,y=s-b,z=s-c)，用命令xtos实现.命令为：

>read “d:/sjxbzyz.txt”;#打开三角形几何量数据库#

>df∶=%;#将数据置入变量df#

>mmb∶=xtos(sqrt(x/4*x^2+5*y*z)));#将(17)式中局部项转化为三角形几何量#

>zjbj_otfqdcs({mmb},df,0,0,1,1,1,1);#在库中进行搜索#

执行上述命令后输出若干结果，用glzdpfdeg找出次数最低者(为10次)，并用aptoxp命令将其化为代数不等式，得

(17′)

(17′)就是不等式(17)的局部对称不等式，且容易配平方证明.

文献[16]指出：三角形是3 元代数系统的一个模型，例17再次说明，如果能够善于应用这种模型，则可能会解决较复杂的问题.

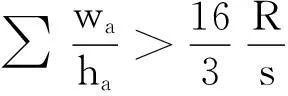
参考文献：

[1] 刘保乾.不等式的自动发现原理及其实现[J].汕头大学学报,2011，26(2)：3-11.

[2] 刘保乾.不等式自动发现和判定程序agl2010的若干改进及应用[J]. 广东第二师范学院学报，2011，31(3)：13-22.

[3] 刘保乾.再谈不等式自动发现与判定程序agl2010的改进和应用[J] .汕头大学学报.2012，27(1)：14-23.

[4] 刘保乾.Si类多项式初探[J].广东教育学院学报，2007,27(5): 6-13.

[5] 刘保乾.多项式分拆初探[J].广东教育学院学报，2007,27(3): 5-12.

[6] 刘保乾.局部对称多项式线性空间初探[J].广东教育学院学报，2008,28(5)：10-16.

[7] 陈胜利，姚勇．实对称型上的Schur子空间及应用[J]．数学学报， 2007，50(6)：1331-1349．

[8] 刘保乾.生成运算及其在证明多元对称不等式中的应用[J].广东教育学院学报，2005,25(3)：10-14.

[9] 刘保乾．智能模拟思想应用3例[J]．广东第二师范学院学报,2014,34(3):6-14.

[10] 隋振林．一个求线性方程组非负解的通用程序[J]．广东第二师范学院学报，2013，33(3)：32-35.

[11] 刘保乾． 随机数验证程序在多项式非负分拆中的应用[J]．汕头大学学报(自然科学版)，2012，27(3)：27-37.[12] 刘保乾.局部对称多项式线性空间初探[J].广东教育学院学报，2008,28(5)：10-16.

[13] 刘保乾. 多项式非负分拆算法的若干改进和补充[J].汕头大学学报，2013，28(3)：18-28.

[14] 刘保乾. 磨光集及其应用[J].汕头大学学报，2015 ,30(2):44-55.

[15] 刘保乾. 两个不等式通用模型及其应用[J]. 广东第二师范学院学报，2013，33(3):14-24.

[16] 刘保乾.四边形不等式的自动发现[J]. 汕头大学学报,2012，27(2)：9-17.

收稿日期：2016-02-24

作者简介：刘保乾，男，陕西凤翔人，西藏自治区组织编制信息管理中心工作人员.

中图分类号：O 122.3

文献标识码：A

文章编号：2095-3798(2016)03-0013-10

9 Typical Examples in Inequality’s Program Agl2012 for Discovery and Decision

LIU Bao-qian

(Tibet Autonomous Region Information Management Center of Authorized Strength’s Organization, Lhasa, Tibet, 850000, P.R.China)

Abstract:There are 9 examples of application with inequality’s program Agl2012 for discovery and decision in this paper. These examples show the powerful function of software. On the one hand, it was provided for ready-made templates and reference for research and application. On the other hand, it was summarized for strategies and technique of software use. So some corresponding research subjects were proposed. Some research fields were initiated, for example, the local symmetry of product inequality. There are some new results and outstanding questions.

Key words:automated inequality discovering; program agl2012; question.