弧线足球的数字仿真

林佩珠

(广东第二师范学院 物理与信息工程系， 广东 广州 510303)



弧线足球的数字仿真

林佩珠

(广东第二师范学院 物理与信息工程系， 广东 广州 510303)

摘要:在现有文献基础上对弧线足球的研究进行了两方面的改进:考虑了空气阻力矩; 足球转动轴不再局限于竖直方向. 这些改进使得本文所模拟的物理条件更接近实际，而且能够比较各种不同初始角速度0的足球运动规律. 我们先推导出足球的动力学微分方程组, 进而用标准的数值方法求解微分方程组、给出足球飞行的动画片. 选择三种典型的初始角速度0进行了具体的数值研究, 数值结果表明：以相同的初速度0踢出足球, 对应于不同的初始角速度0, 足球的运动情况有明显的差别. 对于相同的 m/s，当无旋转ω0=0时，足球的轨迹是平常的抛体运动轨迹；当rad/s时，足球的轨迹是典型的香蕉球轨迹；当 rad/s时，足球的轨迹呈现出左右飘动的现象，类似于落叶球.

关键词:足球；旋转；马格努斯效应；弧线球; 数字模拟

0引言

弧线足球是运动和学术界感兴趣的话题. 文献[1-3]从力学角度，对弧线足球进行受力分析，定性地解释了弧线球的形成机制。实际上,弧线球的定性解析不算复杂：如果球在起飞前，对球施以足够的旋转，球就会沿着曲线飞行. 球旋转时会带着与它接触的那部分空气一起旋转，形成一个跟球一起旋转的附着空气层，所以球的一侧气流运动速度比另一侧的大. 根据流体力学原理，气流运动速度较大一侧的压力较小、气流运动速度较小一侧的压力较大. 球两侧压力不同，使球的运动方向发生偏转，形成弧线球.简言之，弧线球是由于足球在飞行过程中存在自转而引起的.但是，要定量计算出给定初始条件的具体运动规律却是一个复杂的问题. 为了便于计算，文献[4]和[5]做了一系列简化，忽略了空气阻力矩和竖直方向的空气阻力，并限制转动轴为竖直方向，这与实际情况有较大的差距；文献[6]改进了文献[4]和[5]的一个不足,考虑了竖直方向的空气阻力.

本文在文献[4-6]的基础上进一步考虑空气阻力矩,转动轴也不再限制于竖直方向，使物理模型更加接近实际情况；用标准的数值方法求解动力学微分方程组，比较三种不同旋转速度的足球的运动规律，并用动画方式定量模拟弧线球的三维运动轨迹.

1动力学微分方程组

使飞行中自转的球发生偏转的力称为马格努斯力，其大小和方向由下式给出[4-6]

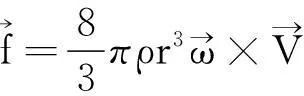
(1)

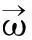
即

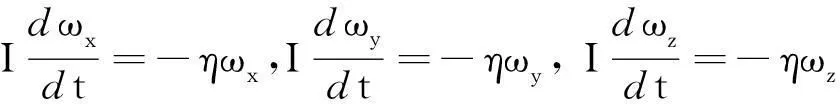
(2)

解方程组(2)得

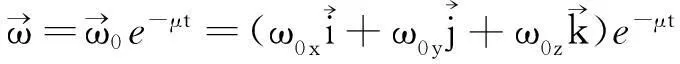
式中μ=η/I. 所以，式(1)可改写成

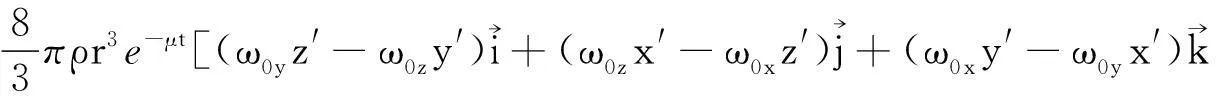
(3)

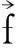
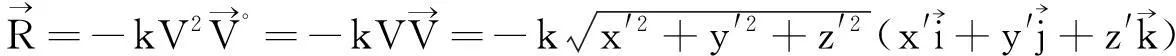
(4)

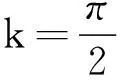
把式(3)和式(4)及重力代入牛顿第二定律，得到足球动力学方程组：

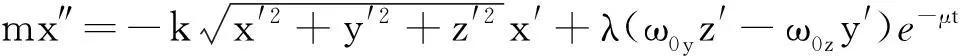
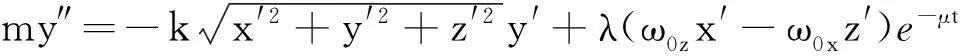
(5)

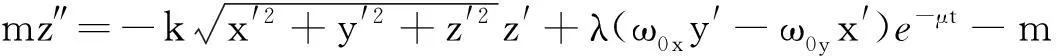
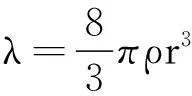
2足球运动规律的数值模拟

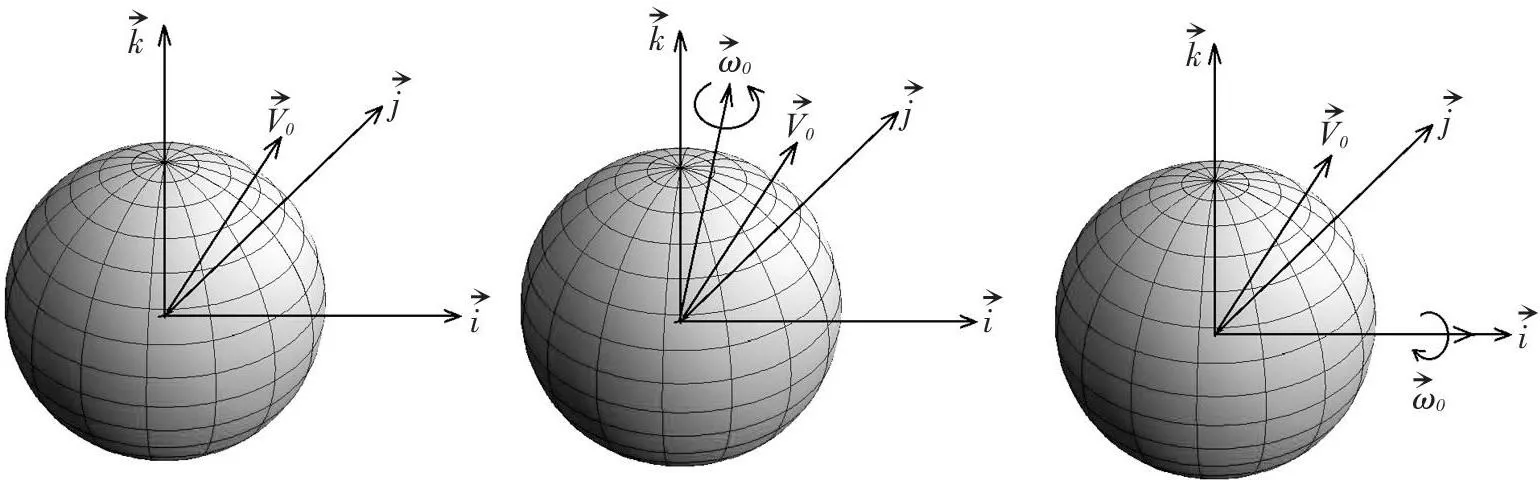
kjiiijkω0kjω0V0V0V0

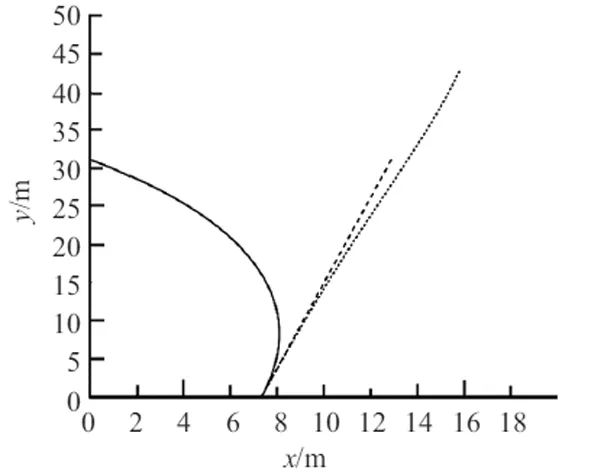
图2　三种情况下足球轨迹在水平面内的投影长划线：无旋转ω0=0；实线短划线

1) 当ω0=0时，足球到达最高点的时间为0.836 95s、落地时间为1.811 3s、最大高度为4.097 4m，运动轨迹在xoy平面和yoz平面内的投影分别如图2和图3的长划线所示，轨迹在xoy平面的投影是一条直线，足球轨迹是垂直于地面的平面曲线.

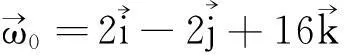
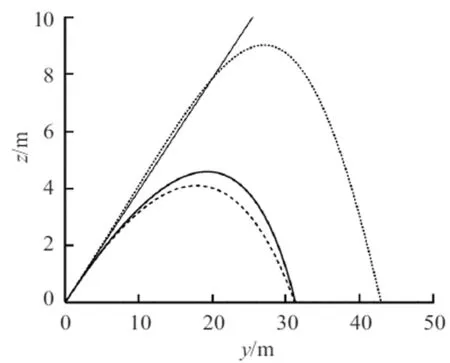
图3　三种情况下足球轨迹在yoz平面内的投影细实线：出射方向; 长划线：无旋转ω0=0；粗实线短划线

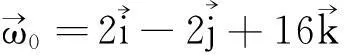
t=0.924111s024681012141618x/m302520151050543210y/mz/mt=1.81522s30252015105y/m0543210z/m024681012141618x/m图4 当ω0=2i-2j+16k时,足球在最高点附近的位置以及所经过的轨迹 图5 当ω0=2i-2j+16k时,足球入网前夕的位置以及所经过的轨迹

024681012141618x/mt=1.67435s109876543210z/m30252015105y/m045403530252015105y/m0454035109876543210z/m024681012141618x/mt=3.46416s图6 当ω0=13i+0j+0k时,足球在最高点附近的位置以及所经过的轨迹 图7 当ω0=13i+0j+0k时, 足球落地的位置以及所经过的轨迹

3结论

当无旋转ω0=0时，足球的轨迹是平常的抛体运动轨迹；

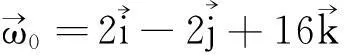
109876543210z/m-12-7-23813182328y/m-10-8-6-4-202468x/mt=3.34869s

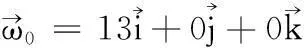
参考文献：

[1] 徐庆玉，侯振福，杨怀英.对足球弧线球的力学分析及训练[J].山东轻工业学院学报,1995,(4):69-70.

[2] 罗英和，马硕章.浅谈足球的弧线运动[J].南宁师范高等专科学校学报,2008(2):125-126.

[3] 王伟,刘欣.浅谈“香蕉球”的力学原理[J].体育科技文献通报，2008(3)：25,43.

[4] 葛隆祺，叶卫军. 足球旋转球的运动规律[J]. 物理通报, 1999 (2):7-8.

[5] 马涛. 数字化大学物理[M]. 浙江: 浙江大学出版社, 2008:116-119.

[6] 江俊勤. 基于Mathematica的数字化物理学[M]. 北京：科学出版社，2015:141-145.

收稿日期：2016-03-04

基金项目：广东省高等学校物理专业综合改革试点项目(XM060012物理学)

作者简介：林佩珠，女，广东揭阳人，广东第二师范学院物理与信息工程系实验师.

中图分类号：O31；G846

文献标识码：A

文章编号：2095-3798(2016)03-0063-05

The Digital Simulation of Banana Kick

LIN Pei-zhu

(Department of Physics and Information Engineering, Guangzhou University of Education,Guangzhou, Guangdong, 510303， P.R.China)

Abstract:On the basis of the existing literature about Banana kick research, we have made two improvements: Air resistance moment is considered; Football's rotation axis is no longer limited to the upright direction. So, the physical condition of the digital simulation in this paper is closer to the actual situation and the motion laws of the football in a variety of different initial angular velocity 0 can be compared. The dynamical differential equations of the football are derived, and then are solved by using standard numerical method. The animation of the football motion is given. In this paper, the numerical study about three typical initial angular velocity 0 was carried out. The results show that the motion of the football is obviously different with the same initial velocity0and different0. For m/s， the motion trajectory is a trajectory of the usually projectile motion when ω0=0; the motion trajectory is a typical trajectory of banana kick when rad/s; the motion trajectory shows a left fluttering-right fluttering phenomenon (similar to falling leaf) when rad/s.

Key words:football; rotation; Magnus effect; banana kick; digital simulation