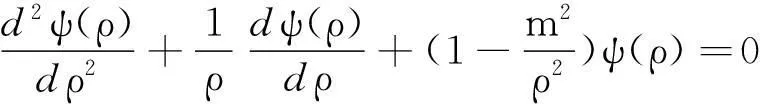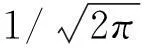有限高量子围栏中电子的能级和波函数

江俊勤

(广东第二师范学院 物理与信息工程系， 广东 广州 510303)



有限高量子围栏中电子的能级和波函数

江俊勤

(广东第二师范学院 物理与信息工程系， 广东 广州 510303)

摘要:用数值分析的方法对有限高量子围栏内电子的能级和波函数进行全面的研究，纠正了现有文献中的一些纰漏. 借助Mathematica强大的计算能力和杰出的数字绘图功能，给出了能级图和三维概率分布图.

关键词:有限高量子围栏; 修正的贝塞尔函数；能级; 概率分布

1993年，克罗米(M. F. Crommie)等人使用扫描隧道显微镜(STM)将48个铁原子吸附在铜表面上并排列成一个半径为71.3 Å的圆环，铁原子的平均间距为9.5 Å，这个原子圆圈能将铜表面上的电子围住，所以这样的原子圈被称为“量子围栏”或“原子围栏”，该实验通过STM观测到了围栏内电子概率的驻波图.

这是人类第一次直接观测到的电子驻波图，对于物理学的理论和应用都具有极其重要的意义，因此已有多位作者通过求解定态Schrödinger方程来解释围栏内电子的驻波现象，文献[1]把问题简化为无限高围栏并计算了电子的能级和波函数, 但是无限高围栏显然与实际量子围栏存在差距；文献[2]和[3]考虑了有限高围栏，但由于围栏的外面是无限的自由平面，电子不被围栏束缚、其能量不能具体确定；文献[4]讨论了高度有限而厚度无限的围栏模型，这样的量子围栏能把能量低于围栏高度的电子束缚在其内部，电子具有确定的能级和本征波函数，可惜的是文献[4]没有对电子的能级和状态进行全面的研究，而且计算过程存在多处纰漏.

本文借助Mathematica强大的计算能力和杰出的数字绘图功能，对高度有限而厚度无限的围栏内的电子态进行全面深入的研究：纠正了文献[4]的一些纰漏、 讨论能级数目与围栏尺寸的关系、绘制出能级图和三维概率分布图.

1 定态Schrödinger及其贝塞尔函数解

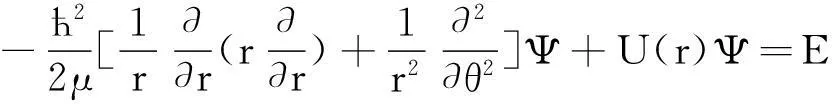
(1)

用分离变量法求解，令Ψ=ψ(r)Φ(φ)，代入(1)式，得

(2)

和

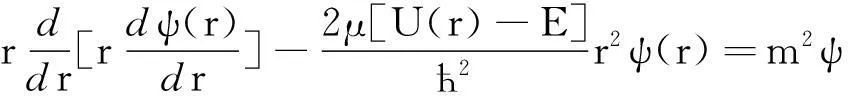
(3)

(2)式的解为

(4)

式中,m为角量子数(决定轨道角动量的大小)，由波函数单值性的要求Φm(φ+2π)=Φm(φ), 可得m=0,±1,±2,…； |m|的最大值由R和U0的大小决定，具体取多少，将在后面进一步讨论.

圆内外的势能不同，(3)式必须分两个区域求解.

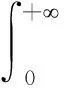
当0≤r

(5)

式(5)是标准的贝塞尔方程，有两个独立的解Jm(ρ)和Ym(ρ)，分别为第一类贝塞尔函数和第二类贝塞尔函数.

但是Ym(0)→-，不符合波函数有限性要求(ψ(0)=有限值)，所以符合波函数有限性要求的解为

ψ(ρ)=c1Jm(ρ)(0≤r

当r≥R时, 若令β2=k2(U0-E)，ρ=βr，则

(6)

式(6)也有两个独立的解Im(ρ)和Km(ρ)，分别称为第一类修正的贝塞尔函数和第二类修正的贝塞尔函数.Im(+)→, 不符合波函数要求，所以符合波函数要求的解为ψ(ρ)=c2Km(ρ)(r≥R).

这是关于c1和c2的齐次线性方程组，有非零解的条件是系数行列式值等于0，

这是决定能量本征值的条件，求其数值解就可求得体系的能级. 第一个方程左边接近于0，会影响计算精确度；第二个方程分母多处为零，会干扰正常计算；第三个方程最优越，令

(7)

则体系的能级为f(E)=0的根. 体系的径向波函数可写成

(8)

几点说明：

(iii) 由于J-m(ρ)=(-1)mJm(ρ),K-m(ρ)=Km(ρ)，从式(7)和式(8)可知-m和m所对应的能级和径向波函数是相同的，但是每一个能级有两个角向波函数e±i|m|φ，所以能级是二度简并的(m=0除外)；由于m的正负不影响能级和概率分布，所以在具体计算时可以只考虑m=0,1,2,….

2能级的数值结果

下面以Mathematica为工具，取围栏的半径为R=71.3 Å、围栏的高度为U0=0.5 eV，对围栏中电子的能级和波函数进行具体计算，并绘制概率分布图.

图1　当R=71.3 Å，U0=0.5 eV,m=0时f(E)的曲线图

对应于m=0，f(E)的曲线如图1所示. 在[0, 0.05]内E0初值太接近，可放大该区间再画另一幅f(E)曲线图(略)，从而确定E0的8个初值分别为0.004，0.022，0.052，0.09，0.16, 0.23, 0.32和0. 41(曲线在0.5处并未与横轴相交).

图2　当R=71.3 Å，U0=0.5 eV时f(E)的曲线实线:m=10；长划线:m=21；短划线:m=22

对于m=1,2,…的情况，用同样的步骤逐一绘制f(E)的曲线图，结果发现: 对于固定围栏半径R和高度U0，随着m的增大f(E)=0的实根个数逐渐减少；对于R=71.3 Å和U0=0.5 eV，当m=10时只有四个实根(E=0不是本问题的解，不计算在内)，当m=18～21时都只有一个正实根(与横轴正向只有一个交点)，从m=22开始没有实根，图2给出了m=10，21和22时f(E)的曲线. 所以对应于这样的围栏参数，角量子数的取值范围为m=0,±1,±2,…,±21(对应的初值不在这里一一列出).

表1 给出了m=0,1,2,…,21所对应的能级个数(-m与m的能级数相同).

表1　有限高量子围栏(R=71.3 Å和U0=0.5 eV)的角量子数及其能级个数N

所以当R=71.3 Å和U0=0.5eV时，能级个数为90；围栏半径R或者高度U0越大，m的取值范围就越大. 如果把围栏高度近似简化为无限高，则m的取值范围就是无穷(一切整数)，这就是文[1]的情形.

有了能级的大概值(找根的初值)，就可以寻找当R=71.3 Å和U0=0.5eV时m=0,1,2的能级了.对应于m=0的能级(以eV为单位，下同)分别为: 0.004 016 71, 0.021 154 6, 0.051 947 5, 0.096 326 5, 0.154 16, 0.225 217, 0.309 051和0.404 554；

图3　前三个角量子数的能级总图实线,长划线，短划线分别对应于m=0,1,2

对应于m=1的能级分别为: 0.010 196, 0.034 158 8, 0.071 757, 0.122 887, 0.187 376, 0.264 909, 0.354 822和0.454 964；

对应于m=2的能级分别为:0.018 3131, 0.049 154 6, 0.093 557 3, 0.151 414, 0.222 503, 0.306 39和0.402 018.把m=0,1,2三种不同角动量的能级画在一起，得如图3所示的能级总图.

对于m=0,1,2三种不同角量子数，能级是很有规律的：从低到高分别是m=0,1,2的三个最低能级(m=0的第一个能级为基态能)，接着是m=0,1,2的三个次低能级(m=0的次低能级略高于m=2的最低能级)，…，最后是m=0的第八个能级及m=1的第八个能级．

如果把m=3,4,…,21的能级也一起排列，情况就复杂了，具体情况有待进一步计算.

3波函数与概率分布的数值结果

把已经得到的能级逐个代入式(8)即可确定每个能级所对应的波函数，借助Mathematica可以自动快速得到波函数，并绘制电子的概率分布图(立体图)，对于m=0，R=71.3 Å和U0=0.5eV，如图4～图11所示. 对于m=1，只给出第四个能级所对应的电子概率分布图，如图12所示；对于m=2，只给出第三个能级所对应的电子概率分布图，如图13所示.

以上结果表明：角动量为零 (m=0) 的量子态在围栏中心(r=0)是概率主峰，角动量不为零 (m≠0) 的量子态在围栏中心(r=0)是概率低谷(波函数的节点). 此外，不论角量子数m是多少，概率分布图的波峰个数都与能级E(m,n)的序号n相一致.

最后，研究束缚态的最高能级(m=21, 即能量最接近0.5eV)的量子状态，数值结果如图14所示. 电子概率分布主要集中在围栏边缘.

图14m=21的能级(唯一且最高的能级)所对应的概率密度

参考文献：

[1] 周佩瑶，王莱，陈宜生. 原子围栏中金属表面电子的态函数及能级[J]．工科物理，2000，10(4)：9-11.

[2] 戴淇, 蒋平. 量子围栏的电子结构(英文)[J].复旦学报(自然科学版), 2000, 39(2):132-134.

[3] 塔立, 单嵛琼, 周向仁, 等. 量子围栏中的表面电子局域态密度及其模拟[J]．云南大学学报(自然科学版)，2009，31(S2)：411-416.

[4] 董建．Mathematica与大学物理计算 [M]．2版. 北京：清华大学出版社，2013：289-296.

收稿日期：2016-01-21

基金项目：广东省高等学校专业综合改革试点项目(2014)

作者简介：江俊勤，男，广东揭阳人，广东第二师范学院物理与信息工程系教授.

中图分类号：O562.1

文献标识码：A

文章编号：2095-3798(2016)03-0057-06

Energy Level and Wave Function of Electron inside Finite High Quantum Corral

JIANG Jun-qin

(Department of Physics and Information Engineering, Guangdong University of Education,Guangzhou，Guangdong, 510303, P.R.China)

Abstract:The energy levels and wave functions of the electron in the finite high quantum corral are numerically studied. Some errors in the existing literature are corrected. The energy level diagrams and the three dimensional probability distribution diagrams are given by using MATHEMATICA.

Key words:finite high quantum corral; modified Bessel function; energy level; probability distribution