关于数学学法指导的一些尝试

黄雪娟

【摘要】 本文从学生学习数学的学法指导方面介绍了笔者在教学中的一些尝试和做法.

【关键词】 学法指导；数学教学；学习方法

学法指导，是教师运用教育学、心理学等教学原理对学生进行学习方法的指导，是学生“学会学习”的重要组成部分. 数学学法指导应该着重指导学生学会理解数学知识、解决数学问题，学会数学思维，学会数学交流. 因此，如何在数学教学中开展学法指导，寓学法于教法之中，从而指导学生改变学习方式，让学生学会学习，提高学生的学习效率，是实现教学质量提高的突破口. 以下是笔者开展学法指导的一些做法.

1. 学生自学方法的选择与指导

提供具体的自学方法与指导，供学生选择应用，在应用中触类旁通地形成自学的能力.

（1）信息收集法：对于教材上一些定理、概念的学习，教师从中指导学生收集相关信息、信息处理的方法，从而事先获得知识.

例如，在进行勾股定理教学时，教师布置预习作业并要求学生收集有关勾股定理的历史资料、勾股定理的证明方法，从而明确勾股定理研究的对象和获得的结论. 学生通过自学阅读教材、上网和去图书馆收集资料，获得了很多的历史资料信息，并提交了多种证明方法. 学生在课堂交流证明方法的同时，已基本掌握了勾股定理教学中要学习的内容.

（2）设问探究法：教师根据学生学习能力的差异性，指导学生在自学过程中從数学知识、技能、思想等各方面思考、设置问题，自己探究知识的生成过程，从而提高预习和课堂听课的效果.

例如，在实数概念教学时，老师要求学生预习教材内容，启发学生在预习过程中要善于提出问题，或自己解决问题，或提交老师帮助解决问题. 在课堂上交流时，能自行解决的问题：分数、有理数、无理数、绝对值及实数的概念；不能解决的问题：如何进行实数大小比较中无理数之间、有理数与无理数之间的大小比较？教师对学生基本能解决的问题通过出一些题目进行辨析巩固，对未能解决的问题和教学中的难点通过课件展示进行化解，从中揭示数形结合、类比、分类的数学思想方法，指导学生更科学、有效地学习.

（3）类比研究法：教师启发指导学生运用类比原理对类比对象的学习、研究方法进行新知识生成过程的探究.

例如，教师布置预习反比例函数任务并启发：我们刚学习了正比例函数，请同学们回去以后，先研究一下反比例函数，你们认为从哪几个方面研究？参照什么研究？通过教师的启发，学生运用知识的迁移，找到了类比的对象是正比例函数. 学生通过自学教材，类比正比例函数的研究方法自主研究反比例函数的相关内容（如表），提交课堂并交流完善.

（4）操作发现法：在数学学法指导中，一要重视学具的操作（可要求学生尽可能多地制作学具、操作学具）；二要重视学生的言语表达交流（给学生尽可能多地提供言语交流的机会，可以是教师与学生间的交流，也可以是学生与学生之间的交流）. 教师指导学生如何自建道具、操作道具，自行发现、猜测、归纳获得的结论，如圆锥、圆柱等的制作.

2. 多种新型教学方法组合应用，开展学法指导

（1）自主探索式教学

“自主探索式”教学为学生主动学习、体验学习过程创设合适的问题情境，充分调动学生的学习积极性，通过提出问题——自主探索——猜想结论或找出方法——交流修正——解决问题的学习过程，引领学生自主探究，学会学习和思考，掌握科学研究的规律.

如，在“直角三角形30度角所对的直角边等于斜边的一半”定理教学过程中，我就采用了自主探索法. 步骤如下：

① 提出这节课研究“直角三角形30度角所对的直角边与斜边的数量关系”这个问题.

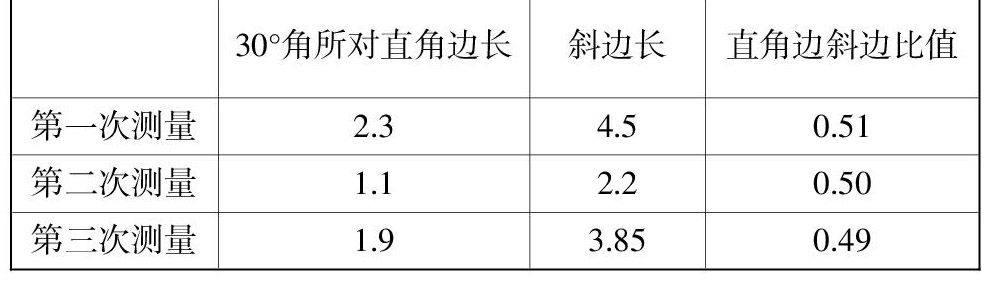
② 让学生任意画三个含30度角的直角三角形，测量30度角所对的直角边和斜边的长度，随机抽问几名学生，并完成数据积累.

③ 让学生观察比值，引导学生分析数据，用归纳的方法猜想：在直角三角形中，含30度角的直角边与斜边的数量关系怎样？

④ 小组交流修正.

⑤ 验证结论.

（2）抛锚式教学

“抛锚式”教学是基于逼真情境的问题解决模式，它建立在有感染力的真实事件或真实问题的基础上. 通过确定真实事件或真实问题（比喻为“抛锚”），从而确定教学内容和教学进程（就像轮船被锚固定一样）. 这种教学模式密切了数学应用问题与现实生活的联系，通过对真实问题情境的体验和感悟，指导学生从已有的知识经验出发，把数学应用问题建模数学化，从而掌握解决数学应用问题的科学方法.

（3）现代信息技术与学科的整合

信息技术与学科的整合，改善了数学课堂教学过程，帮助学生理解数学知识的本质和提高数学应用的能力. 借助于媒体教学，由静态变动态、由数字变图像、由抽象变具体，既提高了课堂教学的趣味性，又拓展了学生思维的空间，改变了学生学习方式.