尝试多种解法 培养创新素养

⦿ 湖北省武汉市第一初级中学 周静秋

1 试题呈现

例如图1,过弦AB的一端点B作一切线BC,过另一端点A作BC的垂线AC与圆O的直径AD.

图1

求证:∠DAB=∠BAC.

2 试题特点

这是一道典型的传统意义上的圆与切线的几何证明题,图形简单,条件明了,富有美感.它以最常见的圆、切线、直径、垂线等几何元素组合成几何图形,求证角平分线.从不同角度去理解基本图形,构造辅助线,发现多种解法,可以培养学生的理性思考能力.解答时需运用转化与化归、数形结合等数学思想及模型观念,将基本图形与几何性质、定理完美结合.较好地考查学生的几何直观、推理能力、模型观念、应用意识、创新意识等数学核心素养.

3 多向解答

如图2,连接BD,由AD是直径,出现90°的圆周角;同时出现弦切角,则∠1=∠DAB,即“同弧所对的圆周角等于它所夹的弦切角”.具体证明如下:如图2,连接BO,并延长BO交⊙O于点F,连接BD,DF.由切线性质,得∠DBF+∠1=90°.由BF为直径,得∠DBF+∠F=90°,所以∠1=∠F.由“同弧所对得圆周角相等”,得∠F=∠DAB,所以∠1=∠DAB.同样弦切角∠2=∠ADB,后面有的证明需反复用到,行文过程不再重复.

图2

分析一：由直径得∠1+∠2=90°,由弦切角得∠1=∠DAB,由直角三角形得∠2+∠BAC=90°,所以得证.

证法一：连接弦,证同角的余角相等.

如图2,连接BD.

∵AD是⊙O的直径,

∴∠ABD=90°.

∴∠1+∠2=90°.

∵BC切⊙O于点B,

∴∠1=∠DAB.

∴∠DAB+∠2=90°.

∵AC⊥BC,

∴∠BAC+∠2=90°.

∴∠DAB=∠BAC.

点评：证法一主要用到了“直径所对的圆周角等于90°”,切线的性质,“同弧所对的圆周角等于它所夹的弦切角”,最后以“同角的余角相等”结束证明.

分析二：连接BD,过点B作BE⊥AD于点E.由直角三角形和直径得∠3+∠D=∠3+∠2=90°,则∠D=∠2.由弦切角得∠1=∠D,则∠1=∠2,由等角的余角相等,所以得证.

证法二：作垂线,证等角的余角相等.

如图3,连接BD,过点B作BE⊥AD于点E,则∠3+∠D=90°.

图3

∵AD是⊙O的直径,

∴∠3+∠2=90°.

∴∠2=∠D.

∵BC切⊙O于点B,

∴∠1=∠D.

∴∠1=∠2.

又∠1+∠BAC=90°,∠2+∠BAD=90°,

∴∠BAD=∠BAC.

点评：证法二主要用到了“直径所对的圆周角等于90°”,直角三角形两锐角互余,“同弧所对的圆周角等于它所夹的弦切角”,最后以“等角的余角相等”结束证明.

分析三：如图4,连接DB并延长,与AC的延长线交于点F,则∠ABF=∠DBA=90°,进而证明∠DAB=∠BAC.

图4

证法三：补全图形,用三角形内角和证明.

如图4,连接DB并延长,交AC的延长线于点F.

∵AD是⊙O直径,

∴∠ABF=∠DBA=90°.

∴∠1+∠2=90°.

∴∠BAC+∠F=90°.

∴∠1=∠F.

∵BC切⊙O于点B,

∴∠1=∠D.

∴∠D=∠F.

∴∠DAB=∠BAC.

点评：证法三主要用到了“补形法”,运用“直径所对的圆周角等于90°”、弦切角、“直角三角形的锐角互余”实现证题.

分析四：图形中出现一条切线,过点A作⊙O的切线,运用切线长定理及切线的性质来证明.

证法四：作切线补全图形.

如图5,过点A作⊙O的切线,交BC的延长线于点E.

图5

∵EB切⊙O于点B,

∴EA=EB.

∴∠EAB=∠EBA.

∵EA切⊙O于点A,

∴∠EAB+∠DAB=90°.

∵AC⊥BC,

∴∠EBA+∠BAC=90°.

∴∠DAB=∠BAC.

点评：证法四主要用到了“切线法”,运用切线长定理、等腰三角形、“直角三角形的锐角互余”来实现证题.

分析五：图形中出现一条切线,连接切点与圆心,由切线的性质得OB⊥BC,则OB∥AC,再运用平行线与等腰三角形的性质即可证题.

证法五：连接切点与圆心.

如图6,连接OB.

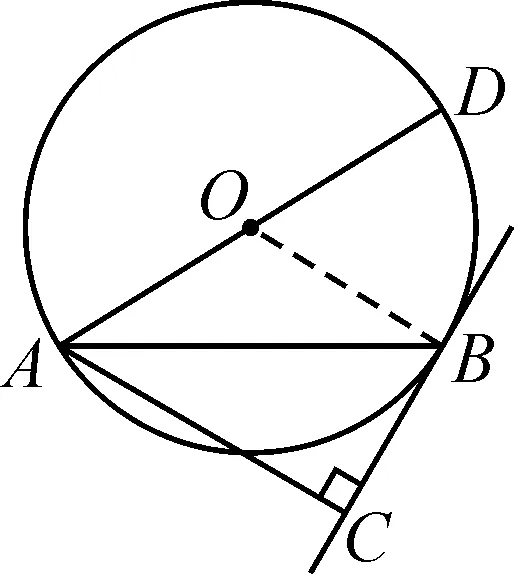
图6

∵BC切⊙O于点B,

∴OB⊥BC.

又AC⊥BC,

∴OB∥AC,

∴∠BAC=∠OBA.

又OA=OB,

∴∠OAB=∠OBA.

∴∠DAB=∠BAC.

点评：证法五思路简单,简洁明快,主要运用切线性质、平行线、等腰三角形来实现证题.连接切点与圆心,是常见的辅助线添加方式.

分析六：图形中出现直径,连接BD,出现直角;作弦的弦心距,出现平行线,再运用平行线与弦切角性质可以证题.

证法六略.

4 变式探究

著名数学家希尔伯特说过:“一个问题的解决,意味着一系列新的问题诞生,当我们解题成功时,不要忘记了提出新的问题”.因此,要不断提出“问题”,“问题”是思维活动进行的原动力和牵引力,通过变式探究,设计有序、逐层递进的问题,可以把知识内容和内在逻辑衔接起来,丰富数学核心素养.

变式1如图7,在△ABC中,CA=CB,D为AB的中点,⊙D与AC相切于点E,求证:BC与⊙D相切．

图7

证明：如图8,连接DE,CD,过点D作DF⊥BC于点F.

图8

∵CA=CB,DA=DB,

∴CD平分∠ACB.

∴DE=DF,且DE为⊙D的半径.

∴BC与⊙D相切于点F.

注：也通过可证明△DAE≌△DBF得到DE=DF.

变式2如图9,在△AEC中,以AE为直径的⊙O交CA于点D,DA=DC,过点E作⊙O的切线交AC的延长线于点F.求证:∠AEC=2∠F.

图9

证明：如图10,连接DE.

图10

∵AE是⊙O的直径,

∴∠ADE=90°.

∵D是AC的中点,

∴EA=EC.

∴∠AED=∠CED.

∵∠AEF=∠ADE=90°,

∴∠AED+∠A=∠F+∠A=90°.

∴∠AED=∠F.

∴∠AEC=2∠F.

变式3如图11,在△ABC中,∠ACB=90°,以BC为直径的⊙O交AB于点D,E为AC的中点,连接DE．求证:DE是⊙O的切线．

图11

证明：如图12,连接OD,OE．

图12

∵O,E分别为BC,AC的中点,

∴OE为△ABC的中位线.

∴OE∥AB.

∴∠COE=∠OBD,∠DOE=∠ODB.

∵OB=OD,

∴∠OBD=∠ODB.

∴∠COE=∠DOE.

又OC=OD,OE=OE,

∴△COE≌△DOE.

∴∠ODE=∠OCE=90°.

∴OD⊥DE.

∴DE是⊙O的切线．

5 结语

创新素养能够打破常规,突破传统,具有敏锐的洞察力、直觉力,丰富的想象力,预测力及捕捉机会的能力,等等,使思维具有一种超前性、变通性.从多角度分析、解答同一道数学问题,对促进学生的创新素养起到示范作用.