单元教研的关键：想清目标和削枝强干

陆肄

［摘  要］ 单元教学、整体建构、结构化教学是当前的教研热点，然而也有一些新授课基于单元教学的想法，将单元起始课上成了“压缩饼干”式的全章复习课，说明教师在备课时并没有想清楚目标. 对于整体建构的单元教学起始课，一定要削枝强干，删减一些例题或习题，侧重于带领学生生成新知，建构知识体系.

［关键词］ 单元教学；想清目标；整体建构；精选问题；削枝强干

最近有机会参加一次市级教研活动，一位名师工作室的核心成员执教了一元二次方程的单元教学，课后的评课氛围很好，但是很多教师“点赞式”的评课并不利于参加活动的青年教师的专业成长. 笔者对该课的一些教学设计以及细节处理都有不同的意见，本文整理了该课的观课记录，并围绕单元教学提出一些个性化的建议，以供研讨.

“一元二次方程单元教学”公开课观课记录

引入新知阶段，观课记录.

活动1  已知正方形桌面的面积是2 m2.

教师围绕该问题提出以下系列问题：你能提出与正方形面积有关的数学问题吗？正方形的边长与面积之间有何数量关系？我们可以用什么样的数学式子来描述它们之间的关系？

观课记录  学生面对教师这些开放性的问题，显得有些不适应，不知道教师想要怎样的答案，课堂气氛反而比较沉闷. 直至教师反复提醒、暗示后，才有学生说出教师想要列出的一元二次方程（x2=2）.

简评  课堂教学情境宜简明好懂，而不是故弄玄虚，特别是开课阶段的问题的设问应指令明确，让学生知道如何分析，而不是不知所云，只想着迎合、配合教师说出想要的“答案”，反而出现开课阶段的“冷场”.

活动2  提供3个生活问题，供学生分析.

（1）某矩形花圃一面靠墙，另外三面所围的栅栏的总长度是19 m，花圃的面积是24 m2.你能提出什么数学问题？

（2）某校图书馆的藏书在两年内从5万册增加到9.8万册. 设这两年图书馆的藏书平均年增长的百分率为x. 请列出方程.

（3）如图，长5 m的梯子斜靠在墙上，梯子的底端与墙的距离比梯子的顶端与地面的距离多1 m. 设梯子的底端与墙的距离是x m，请列出方程.

观课记录  教师出示上述问题之后2分钟，就开始一些“系列追问”，比如你能给它们命名吗？（学生很快齐声回答“一元二次方程”）为什么这样取名？回忆之前认识的方程，一元二次方程应该如何归类？类比数、式的学习经验，你觉得方程如何分类？回顾一元一次方程的定义（一般形式）用语言归纳一元二次方程的定义. 类比学习一元一次方程的过程，你觉得我们应该怎样研究一元二次方程呢？

学生在上述问题的追问之下，多有较好的回答，教师也进行了肯定，然后给出一些必要的板书，板书上归纳出一元二次方程的一般形式和相关概念. 学生归纳出形如ax2+bx+c=0（a，b，c是常数，a≠0）的一般形式之后，教师明确了二次项、二次项系数，一次项和一次项系数，还有常数项，随后问学生一元二次方程一般形式中的“a≠0”是否能省略？对常数b，c有限制要求吗？学生都能正确回答.

活动3  安排学生学习“方程的解”？初步感知如何解一元二次方程？

解以下两个一元二次方程：

（1）x2=2；（2）x2+4x=0.

观课记录  学生很快就看出它们的解，教师又开始“系列追问”，比如方程（1）如何解？依据是什么？如何验证它是方程的解？你能解决第二个方程吗？学生的回答也很流畅，教师很满意.

接下来，教师引导学生思考开课阶段提出来的问题，正方形桌面的面积是2 m2，如何求它的边长？

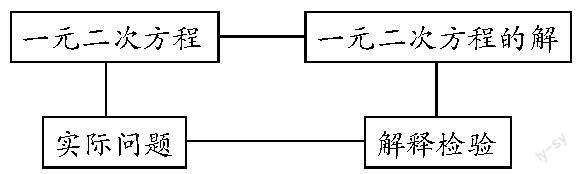
学生很快报出答案，教师很高兴地说，这就是我们本课学习的主要价值——从实际问题到方程的解决思路，然后形成了以下板书：

活动4  运用方程解决实际问题

例题  （以PPT渐次给出题干、后续设问） 一块石头从45 m高的绝壁上落下，变化过程中，石头离海面的高度和下落时间是何种关系？

（1）若时间x（s）分别取0，1，2， 2.5，……

可以发现h（m）对应45，40，25， 13.75，……

观课记录  教师借助列表，帮助学生复习了函数的定义，并让学生列出h与x之间的函数关系式h=-5x2+45.

（2）石头经过多长時间落到海面？

观课记录  教师启发学生，能否用不同的数学语言表述这个问题？学生沉默一会儿后，不太能理解教师的意图，考虑到快要下课了，教师只好给出启发“实际就是令h=0呀，这时能得到怎样的方程”，学生终于说出了一元二次方程0=-5x2+45. 教师肯定了学生的表达，随后进行归纳小结，布置作业，作业设计中除了提到教材上的几个小题，还补充了以下一组习题：

1. 若xm2-2+mx=7是关于x的一元二次方程，求m的值.

以下为选做题：（任选你喜欢的一道题尝试研究）

2. 类比学习“一次函数、一元一次方程、一元一次不等式”的探究经验，尝试解决下列问题.

3. 已知函数y=x2-6x+9，求该函数图象与x轴的交点坐标.

4. 就关于x的方程xm2-2+mx=7改变条件，尝试将其改编成一道求m的值的试题.

简评  这组补充习题不是很恰当，主要理由是第1、4题属于人为编造的“怪怪的”习题，与一元二次方程的学习目标相去甚远，没有必要练习这样的题目. 第2、3题是混淆了新授课与复习题的界限，作为新授课有超前教学之嫌.

关于一元二次方程单元教学的思考

第一，深入研读教材，削枝强干突出重点

备课前要认真研读教材，体会教材内容的主干知识，并联系前后小节进行对比分析，而不是凭感觉，随意增删教材内容. 上文课例中的有些内容属于枝蔓太多，主干不够突出，教师凭自己的经验，随意增设了较多的内容或具有联系的数学知识，误以为关联的内容越多，越能展示教师本人研究本课教学内容的功夫，却没想到走向另一个极端.太多的联系或类比教学，反而让学生的思维难以聚焦于一点，更难以深入想清辨明新知的本质，不利于学生掌握本课内容. 从这个意义上看，很多课时教材内容的简约呈现，甚至只有一两个例题，大抵也是这样的立意.

第二，精选问题情境，减少题量提高品质

数学新知的引入，往往需要选择恰当的问题情境，一般来说教材上的问题情境都是精心选取之后呈现的，教师要重视教材问题情境的运用. 像上文课例中开课阶段（活动1、活动2）选用的几个情境与教材上的情境并不相同，教师可能有自己的构思，但是从教学效果来看，这些情境的新知引入功能并不比教材上的情境好，只是显示了教师似乎不愿意“照本宣科”，而且从一些习题的选取上看，这些习题的品质还有待提升. 比如“活动4”的情境问题中所选的是函数问题，与本节新授课学习一元二次方程新知无甚重要的联系，属于内容效度偏离课时教学目标.

第三，预设教学追问，避免零碎启发思考

精选典型问题驱动教学进程时，预设必要的教学追問往往彰显着教师的课堂驾驭能力. 对于这些课堂追问，教师要有精心预设，不可随着教学进程即兴乱问. 从上文课例中可以看出教师的很多课堂追问都是没有经过充分预设的，即兴追问的可能性很大，教师的数学语言也不够精练. 比如教师在课堂上为了鼓励学生围绕一个数学性质先猜想再证明，即兴举例：“比如要判断一个人的性别，怎么办？（学生不知从何答起）先观察这个人的样子，猜想一下是男是女，接下来是验证，如何验证？（学生更不知道如何回答）拿他的身份证看一下就行了！”教师的即兴举例，不但让学生沉默不言，而且让很多听课教师唏嘘不已. 想起南京大学哲学系郑毓信教授指出的数学教师的三项基本功（善于提问、善于举例、善于比较和优化），“乱举例”现象确实值得大家反思.

第四，明辨单元教学，新授课勿变复习课

当前很多地区在公开课教学或优课评比活动中开展单元教学研究［1］，提倡让学生“先见森林，再见树木”，这样的做法是值得肯定的. 然而，有些教师过犹不及，把单元教学起始课上成了“压缩饼干”式的复习课［2］，这是值得商榷的. 像上文课例中，教师在课堂最后10分钟带领学生思考变量与函数问题，并在最后布置了与二次函数有关的作业，这些做法都说明教师对本课单元教学的目标定位出现了偏差. 单元教学研究首先要想清教学目标，明确教学内容，而不是让与本课内容有关联的习题都出现在教学内容中.

写在后面

本文从一次公开课教学的课例出发，本着研究的心态商榷了单元教学的一些注意事项，文中很多观点带有个性化理解，欢迎同行继续研讨、批评指正.

参考文献：

［1］贾贞锋. 明晰学段要求，践行单元教学——以“与三角形有关的角”单元起始课为例［J］. 中学数学，2018（14）：10-12.

［2］丁振云. 单元教学：从“打包压缩”到“重组学材”——对“二次函数的图像和性质”课例的思考［J］. 中学数学，2020（04）：7-8.