巧用变式教学，优化数学教学

曹炜萍

［摘  要］ 变式教学具有帮助学生梳理数学知识，揭示知识本质的优点，对拓展知识的宽度与深度具有直接影响. 文章从变式教学的本质出发，以一道二次函数题的变式教学为例，具体从“立足方法，促进思维发展”“关注通法，形成变通能力”“注重拓展，发展核心素养”三方面谈谈如何在课堂中巧用变式教学，优化数学教学.

［关键词］ 变式；教学；本质；思维

变式教学在我国应用历史悠久，属于传统教学方式中的一种. 所谓变式教学，是指在保持知识本质不变的前提下，通过问题表达方式、条件、结论以及图形形状、大小、位置等的变化，让学生在“变”中求不变，在求异与思变中灵活思维、建构新知，形成良好的创造力. 教师在课堂上进行变式教学，常涉及三种情况：一题多变、一法多用和一题多解.

变式教学的本质剖析

变式教学并非现代教育改革的产物，它在漫长的历史长河中沉淀并流传至今，且愈发完善，说明这种教学方法具有独特的优越性，对新课改浪潮下的数学教学具有指导意义. 顾明远先生认为：变式教学是指用不同形式的事例或材料阐明事物本质属性的过程，它可以帮助学生更好地把握数学知识，积累学习经验，提升数学思维品质，因此变式教学属于一种本质主义教学.

变式教学在基础知识和基本技能的教学上有着其他教学方式无可比拟的优势与价值，这种教学方式一般在事前就设定好了知识本质，所有教学都紧紧围绕这个“本质”而进行，或者说围绕“本质”进行“削皮”活动. 本质呈现出不同的形态让学生识别，而学生的个体差异在此时并不是最重要的，了解数学事物的本质才是教學目标所在，从这一点上也能看出变式教学本质主义的观点.

本质主义观若使用得当，则能成为课堂教学的助推器，成功激活学生的思维，帮助学生获得事物的本质；若使用不当，则会从一定程度上限制学生创新意识的形成与发展，对教学产生消极影响. 因此，大家进行变式教学时要结合学情与教学内容的特点，选择合适的方式，切不可为了变式教学而变式教学.

变式教学的实施策略

1. 立足方法，促进思维发展

波利亚认为：善于解题才算掌握了数学，加强解题训练是中学数学教学的关键任务. 那么，如何在教学中开展解题训练呢？实践告诉我们，立足解题方法的训练，能充分暴露学生思维的过程，促进学生解题能力的发展. 同时，设计具有一定探究性、开放性的变式题，往往能给学生提供较好的思维平台，尤其在问题链的引领下，学生的思维可朝纵深发展，促进学生观察力、想象力以及转化力的提升.

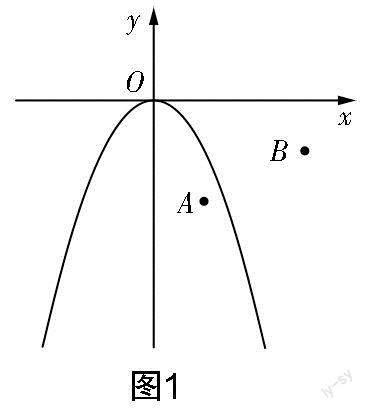
例1如图1所示，在平面直角坐标系xOy中，点A（1，-2），B（3，-1），抛物线y=-x2的图象为l.

问题1：平移抛物线l使其经过点A却不经过点B. ①满足这个条件的抛物线总共有多少条？②如果只向下平移，写出此时经过点A的抛物线的解析式.

问题2：如图2所示，平移抛物线l使其经过点A也经过点B，此时我们得到抛物线l. ①抛物线l的顶点C的坐标和抛物线l的解析式是什么？②△ABC的面积是多少？

问题引导  ①抛物线在平移前与平移后，其特征有什么变化？②与抛物线有关的三角形面积一般是怎么求的？③我们常用哪些特殊点的坐标去刻画线段的长度？

解析问题1  第①问，有无数条抛物线；第②问，设此时抛物线的解析式为y=-x2+c，把点A（1，-2）代入其中可得抛物线的解析式为y= -x2-1.

设计意图本题为一道综合题，涉及的知识点较多，意在引导学生从特殊四边形的几何模型着手进行分析. 教师以几个问题作为学生思维的铺垫，采用低起点、小步子的方法促进学生的思维水平提升，引导学生应用常规的方程思想与数形结合思想解题. 这种解题教学方法的设计，首先为了巩固学生对知识的掌握程度，其次为了向学生渗透研究数学问题的模式与思想方法.

2. 关注通法，形成变通能力

章建跃教授提出：数学教学要注重通性通法的教学，其中，通性泛指数学概念所反映的数学本质，通法为数学思想方法［1］. 通俗点讲，通性就是师生所熟知的且可以大范围使用的明确的结论；通法是在知识结构稳定的前提下，根据通性而获得的，可用来解决一类问题的普通方法. 因此，通性通法不可分割，能够直接帮助学生解题.

掌握通性通法对掌握“四基”与“四能”具有促进作用，对落实“三会”“立德树人”等具有直接影响. 但值得注意的是，通性通法的应用要避免思维定式的形成，否则得不偿失. 实践告诉我们，抓住问题的核心，并探寻出一定的解题思路与方法，对培养学生的数学思维品质（深刻性、灵活性、敏捷性）具有深远的影响.

沿用例1的已知条件：

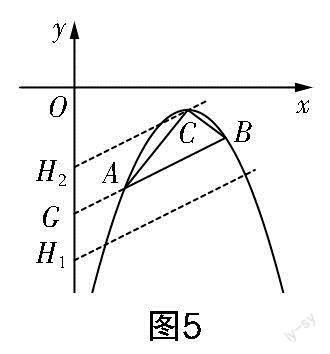
问题3：在y轴上是否存一点H，使得S=S？若存在，求出点H的坐标；若不存在，请说明理由.

问题引导①关于三角形等面积变换，可以应用的几何模型有哪些？②一般情况下，该怎样根据几何图形的特征求解特殊点的坐标？③已知点的对称点一般怎么求？存在什么规律？④可以从什么角度改变思考方向，将陌生复杂的问题转化成我们所熟悉的问题求解？

设计意图  以问题探究的方式引导学生紧扣图形中的关键信息进行分析，通过数形结合思想探寻等面积变换所涉及的基本模式，如此可以巧妙地将原问题转化成直线与坐标轴的交点问题，从而获得利用面积确定点位置的通用方法. 对通用方法的掌握，能为后续解决类似问题奠定方法基础.

3. 注重拓展，发展核心素养

《义务教育数学课程标准（2022年版）》提出：要增强数学综合性的学习，注重学科各部分知识的整合，并倡导推进跨学科知识的拓展，构建综合性的课程［2］. 学科整合理念与数学例题教学拓展有千丝万缕的联系，教师应以例题教学为基础，从多渠道、多领域融合多个知识点，让学生通过综合性问题加强实践训练，实现核心素养的发展.

变式教学中的拓展延伸，意在解决更多更复杂的变式问题，引导学生在变式问题的解决过程中应用类比推理等方法，及时反思解题策略，拓宽解题视野，厘清解题思路，发展数学思维能力.

问题1：在该抛物线上是否存在一点Q，使得S=S. 若存在，求出点Q的坐标；若不存在，请说明理由.

问题2：在该抛物线上是否存在一点M，使得A，B，C，M四点组成一个梯形？若存在，求出点M的坐标；若不存在，请说明理由.

问题3：在抛物线位于线段AB上方的部分是否存在一点P，使得△ABP的面积最大. 若点P存在，求出点P的坐标；若不存在，请说明理由.

问题4：在抛物线对称轴上是否存在一点T，使得△ABT是直角三角形并且斜边是AB. 若存在，求出点T的坐标；若不存在，请说明理由.

问題引导①在分析数量关系时，该如何找到“变”中的“不变”作为解题的突破口呢？②在解题时，该如何以数助形，将图形问题转化成数量问题进行分析呢？③怎样将几何问题转化成适当的数学模型进行数量关系的求解与应用？④在解题过程中，该如何分解几何图形，并从几何图形的特征着手，用函数思想探寻运动变化中的“不变”？⑤该怎样在观察、猜想与验证的过程中，对数学知识形成自己独有的理解，并内化成方法，提升解题能力？

设计意图将直观的几何问题转化成学生所熟悉的代数模型，对学生数学建模能力的培养具有促进作用.在此过程中，学生不仅获得了良好的解题能力，还积累了一定的解题经验，为核心素养的发展奠定了基础.

设计意图将梯形问题转化成抛物线与直线的交点问题，让学生在类比探究中认识基本图形的特征，这是解决此类问题的关键所在.

解析问题3如图8所示，作PK∥y轴，交抛物线于点P，交线段AB于点

设计意图将面积最值问题转化成线段最值问题，通过对二次函数图象与三角形面积的关系的思考，提升学生的抽象能力和观察能力，为接下来数学思想方法的迁移奠定基础.

设计意图辅助变量的设置，不仅为探寻直角三角形三边的数量关系奠定了基础，还简化了问题的难度，揭示了知识的本质.

实践证明，在解题时，我们不能将目光停留在问题的表面，而要通过一定的手段挖掘出问题中所隐藏的通性通法、数学思想方法以及相关知识点，通过问题的拓展与延伸进一步激发问题的教学价值，让学生在变式拓展中深刻体会知识的本质与内涵，从真正意义上掌握解题技巧.

例1和例2所涉及的数学思想方法有数形结合思想方法、化归思想方法、函数思想方法等，这些都是初中阶段重要的数学思想方法，是引领学生突破思维障碍、完善认知结构的基础. 变式教学方法的应用，能让学生将所学的知识整理成完整的知识网络，并通过解题拓宽视野、丰富思维，促进核心素养的形成与发展.

参考文献：

［1］章建跃. 如何帮助学生建立完整的函数概念［J］. 数学通报. 2020（9）：1-8.

［2］中华人民共和国教育部. 义务教育数学课程标准（2022年版）［M］. 北京：北京师范大学出版社，2022.