动静相融通 图形显本质

戴惠

［摘  要］ 以大单元整体化教学对“平行四边形复习课”进行设计，从图形变换的角度整合平行四边形与图形变换知识，加深学生对平行四边形、矩形、菱形、正方形的概念以及它们之间的关系的理解.学生在折A4纸的实践操作中进行直观想象、合情推理、演绎推理，形成平行四边形的整体认识，建构自己的大单元图谱，逐渐形成数学学科核心素养.

［关键词］ 大单元；平行四边形；图形变换；核心素养

在平行四边形复习课中，很多一线教师都会有知识点多且散的教学困惑. 笔者尝试从图形变换的视角，将图形的平移、旋转、翻折与平行四边形进行结构化整合，引导学生了解平行四边形相关知识的产生与来源、结构与关联，帮助学生建构平行四边形的知识结构大单元图谱，培养学生用动态的眼光看待几何问题，形成科学的思维模式. 本节课收到了较好的教学效果，现将教学与思考予以分享，供研讨.

教学流程概述

教学环节（一）：以动成图，重识变换

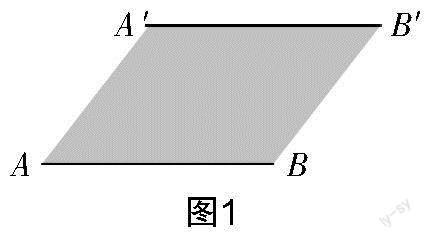
问题1如图1，线段AB=6，将线段AB平移4个单位得到线段A′B′，连接AA′，BB′，

（1）求证：四边形ABB′A′是平行四边形；

（2）求四边形ABB′A′的周长；

（3）若∠A=60°，求四边形ABB′A′的面积.

教学预设学生易得AB=A′B′，AB∥A′B′，根据一组对边平行且相等证得平行四边形，不会继续思考有无其他证明方法. 学生对平移的基本特征中“对应点的连线平行且相等”的理解运用不到位，教师用几何画板演示线段AB平移的过程，启发学生得到AA′=BB′，AA′∥BB′，进而复习两组对边分别平行、两组对边分别相等都是证明平行四边形的方法. 学生能够轻松答对问题（2）（3），复习平行四边形周长和面积公式的同时，活跃本节课的气氛.

问题2如图3，将△OAB绕点O旋转得到△OA′B′，连接AB′，BA′，当旋转角为180°时，

（1）求证：四边形ABA′B′是平行四边形；

（2）△OAB满足什么条件时，平行四边形是矩形、菱形、正方形？

教学预设根据三角形旋转可得△OAB≌△OA′B′，从而得到OA=OA′，OB=OB′，但这里不能说明四边形ABA′B′是平行四边形.  在学生出错后，教师用几何画板演示△OAB绕点O旋转的过程，强调条件中旋转角为180°时，保证A，O，A′三点共线，B，O，B′三点共线，才能证得平行四边形，复习平行四边形的中心对称性和第四种判定方法：对角线互相平分的四边形是平行四边形. 在证明问题2（1）的基础上，学生能很快解决问题2（2），复习矩形、菱形、正方形是特殊的平行四边形.

设计意图区别于先知识回顾，再习题练评的传统的复习课教学模式，以动成图，助力学生重新认识图形边、角之间的关系. 师生在一起解决问题的过程中，唤醒学生记忆，激活学生思维，重构学生知识结构. 同时借助几何画板的演示让学生感悟图形平移、旋转变化的基本特征，从动态的角度再次認识平行四边形的产生与来源，掌握矩形、菱形、正方形是特殊的平行四边形. 在加深学生对矩形、菱形、正方形性质和判定的理解的同时，让学生体会从一般到特殊的研究问题的方法，提升学生分析解决问题的能力.

教学环节（二）：以折为媒，探求本质

活动1拿出手边的A4纸，将A4纸抽象成矩形ABCD，请你折出对称中心O.

教学预设学生容易折出图5、图6的两种折法，在图6中，学生有点O就是对称中心的直观猜想，但在说理方面解释不清. 图7、图8的折法很少学生能够折出，学生从整体对称性的角度认识图形的意识不强.

设计意图数学源于生活又服务于生活， A4纸是学生日常生活中熟悉的材料，折纸活动是学生喜欢的游戏，将A4纸抽象成矩形，转变为教学资源. 学生人人参与折纸，在手脑协同的过程中，复习巩固矩形、菱形的中心对称性和轴对称性，激发了学生学习数学的热情.

活动2在活动1的基础上，请你折出以点O为对称中心的平行四边形.

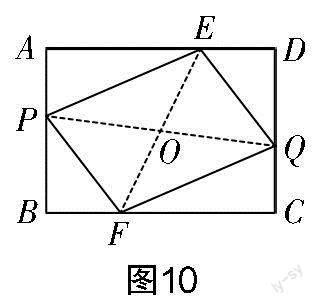
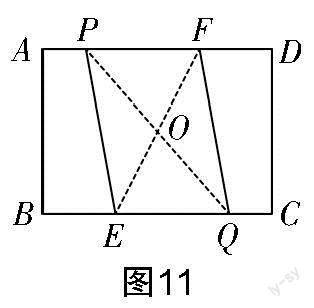
教学预设不少学生能够很快反应出图6、图7、图8折出来的四边形AECF就是平行四边形，教学时安排小组讨论，得到图9、图10、图11的折法. 请小组代表在全班展示，并说出证明方法，发现当折痕过对称中心时，根据对角线互相平分证得四边形是平行四边形.

活动3在活动2的基础上，如何折出菱形？

教学预设学生根据活动1、2的经验，自然联想到只要保证过对称中心O的两条折痕互相垂直，就可以得到菱形.

设计意图根据矩形的对称性设置问题，将折菱形的问题细化，从一般的平行四边形到特殊的菱形，让学生经历由一般到特殊的分析问题的方法. 同时在实际操作中，学生经历了观察猜想、推理验证的活动过程，在自主、合作、交流中不断优化方法，提升思维，形成平行四边形的整体认识.

教学环节（三）：以题为介，加深理解

活动4A4纸的长和宽分别为210 mm×297 mm，我们近似取20 cm×30 cm，如图12，在折出的菱形AECF中，你可以提出哪些问题，如何解决？

教学预设学生提出求线段AC，BE，AE，EF的长度，求菱形AECF的面积、周长等问题. 关注学生的解题方法，鼓励一题多解，引导学生总结几何图形中求线段长的常用方法：勾股定理列方程、等积法、三角函数、相似等.

设计意图对于开放性的试题，每位学生都能发现并提出问题，在一个个问题得到解决后，学生发现图12中所有的量都可求. 在此过程中，学生从做题者变成出题者，增加了学习数学的信心.

活动5如图13，老师将A4纸沿AC对折，点E，F为对应点，连接AE，AF，四边形AECF是菱形吗？连接B′D，你又可以提出哪些新问题呢？

教学预设由轴对称性质，得到对应点E，F的连线被折痕AC垂直平分，只需证明四边形AECF是平行四边形就可证得菱形. 或者根据对应线段、对应角相等，易证四条边相等，从而证得菱形. 学生很容易提出求线段B′D的问题，但在解决上遇到困难. 根据上一问总结的求线段长的方法，发现B′D∥AC，根据△ACF∽△B′DF，求得B′D.

设计意图图12、图13的折法不同，但得到的菱形是相同的，再次巩固菱形的判定方法. 几何图形添加一条线，图形变复杂，研究的量就会多很多，此时从图形整体的角度，从中心对称性和轴对称性的角度思考问题是一条很好的思路，引导学生从更高层面重构知识网络，提升逻辑推理能力.

教学环节（四）：归纳总结，提升能力

教学预设学生根据折对称中心、折平行四边形、折菱形、求线段长等经历，总结知识点；教师引导学生从动态几何问题解题策略、图形变换等角度总结本节课所学内容.

设计意图学生素养的提升来自课后的总结反思. 学生在动手实践中巩固知识，提升能力.

教学思考

1. “动静融通”彰显图形本质

几何学习需要突出图形的形成过程，关注知识应用与发展的完整过程. 本节课之前，学生对平行四边形以及特殊的平行四边形的认识比较单一，能够记忆它们的性质与判定，但不会灵活运用. 本节课通过线段的平移、三角形绕顶点旋转、矩形折纸，在整合平行四边形与图形变换知识的同时，师生共同复习平行四边形这一章节的相关知识点. 教师以平行四边形为依托，在图形变换中以题带点，带领学生再次认识矩形、菱形、正方形是特殊的平行四边形. 在解决问题的过程中学生进行多元化的问题拓展，复习三大变换的性质和平行四边形的相关知识点，重构知识体系.

2. “大单元结构教学”设计几何复习课

温故而知新. 作为复习课，在“温故”的基础上如何引导学生“知新”，如何将复习课上得让学生感兴趣，并且让每一位学生都能有所收获，是备课时笔者遇到的几个难题. 《义务教育数学课程標准（2022年版）》（下称《标准》）指出：在教学中要重视对教学内容的整体分析，帮助学生建立能体现数学学科本质、对未来学习有支撑意义的结构化的数学知识体系［1］. 根据大单元整体教学理念，将初中阶段所学内容进行合理整合，可以有效提高几何复习课的教学效率. 此时需要教师回归课本，研究《标准》，并结合本校学生情况，确定教学目标. 在本节课中，笔者以图形变换为主线，综合考虑不同层次的学生学情，设置出四个教学环节. 每个教学环节均以基础性问题为起点，让学生在动手实践中经历发现、提出、分析与解决问题的过程，梳理了知识、训练了技能，并在最后的综合探究中加深了对知识的理解. 整节课笔者引导学生从“知识—方法—思想”的角度重新审视平面几何问题，对已学知识进行重组和整合，优化原有的知识结构，培养学生的深度思维，提升学生的学习能力.

3. “做数学”助力核心素养的发展

史宁中说：“做数学”的核心在于“做”，实践“做中看”“做中思”“做中说”“做中悟”的过程，实现“促进认知，让学生会学数学；激发情感，让学生愿学数学；启迪智慧，让学生慧学数学；塑造品格，让学生品学数学”. 教师需要充分发掘日常生活中的教学资源，带领学生“做数学”. 如本课中的将A4纸抽象成矩形，学生在折对称中心、折平行四边形、折菱形的过程中思考背后的原理，并用数学语言向全班同学表达自己的观点. 在折纸活动中，人人都可以折，人人都可以提出一些问题，获得数学学习的基本活动经验，激发学习数学的热情.  教学模式从教师的教转变成学生的学，教师对学生提出的稍难的题进行启发引导，在解决问题的过程中学生掌握基础知识和基本技能，培养了空间观念、几何直观、逻辑推理等能力，发展了数学核心素养.

参考文献：

［1］中华人民共和国教育部. 义务教育数学课程标准（2022年版）［M］. 北京：北京师范大学出版社，2022.