遵循建模规律 培养建模素养

张晓笑 郭美华

［摘  要］ 数学建模是高中数学六大核心素养之一，教师应基于建模规律，按照“发现问题—探究问题—解决问题—模型初现—模型完善—模型建立—模型应用”的环节展开教学，尤其要重视“探究问题”和“模型完善”两个环节. 基于建模规律进行“古典概型”的教学设计，应遵循模型的生成规律，注重学生的思维参与，拓宽模型的应用领域，着力培养学生的建模素养.

［关键词］ 数学建模；古典概型；核心素养

问题的提出

数学是现代科学中必不可少的工具，其“源于生活，归于生活”的特点对数学教学提出了很高的要求. 数学建模是从“实际问题”到“用数学”的一个复杂的综合性过程［1］. 若将整个世界划分为现实世界和数学世界，那么数学建模便可以将两个世界打通并建立联系［2］. 因此，数学建模是实现数学学科“工具性”要求的必要手段. 作为中学数学教师，应当按照新课标的要求，基于数学建模规律设计与开展高中数学课堂教学.

古典概型是最简单的概率模型，也是高中生学习概率相关知识的基础模型，是培养学生建模素养的重要载体. 当前，古典概型教学常见的设计思路是：历史背景导入—明确概念形成模型—应用模型解决问题—课堂小结. 其中，在“明确概念形成模型”环节，部分教师对样本空间中的样本点的“有限性”和“等可能性”进行简单说明后便提出古典概型的概念，再就是概念应用. 这种“顺利”的建模过程有可能造成学生数学建模素养的培养效果“大打折扣”.  其一，在建模过程中，学生只是对具体事例本身进行了讨论，通过归纳其样本空间中的样本点的“有限性”和“等可能性”，直接得出古典概型的概念后就是概率计算. 而事实上，得到古典概型的概念应该是探究活动结束后的一种成果，而不是探究活动的起始. 其二，模型一经建立就“完美”，缺乏检验与完善模型的过程. 事实上，数学建模并非从“现实情境”转化为“数学模型”的单向线性过程，而是建立真实世界与数学世界之间可逆的联系，关注抽象出数学问题与解决现实问题的过程［3］. 这意味着，数学建模需要不断地从数学世界返回真实世界中检验结果、完善模型［4］. 因此，古典概型的教学应遵循模型的生成规律，按照“发现问题—探究问题—解决问题—模型初现—模型完善—模型建立—模型应用”的环节展开教学（见图1）.

基于建模过程的“古典概型”的教学设计

1. 情境导入，发现问题

教师导入情境：据说，意大利医生兼数学家卡当曾经研究过一种赌博方法——把两颗质地均匀的骰子掷出去，以每颗骰子朝上的点数之和作为赌博的内容. 已知骰子的六个面上分别標有1～6点. 那么，赌注下在多少点上最有利？

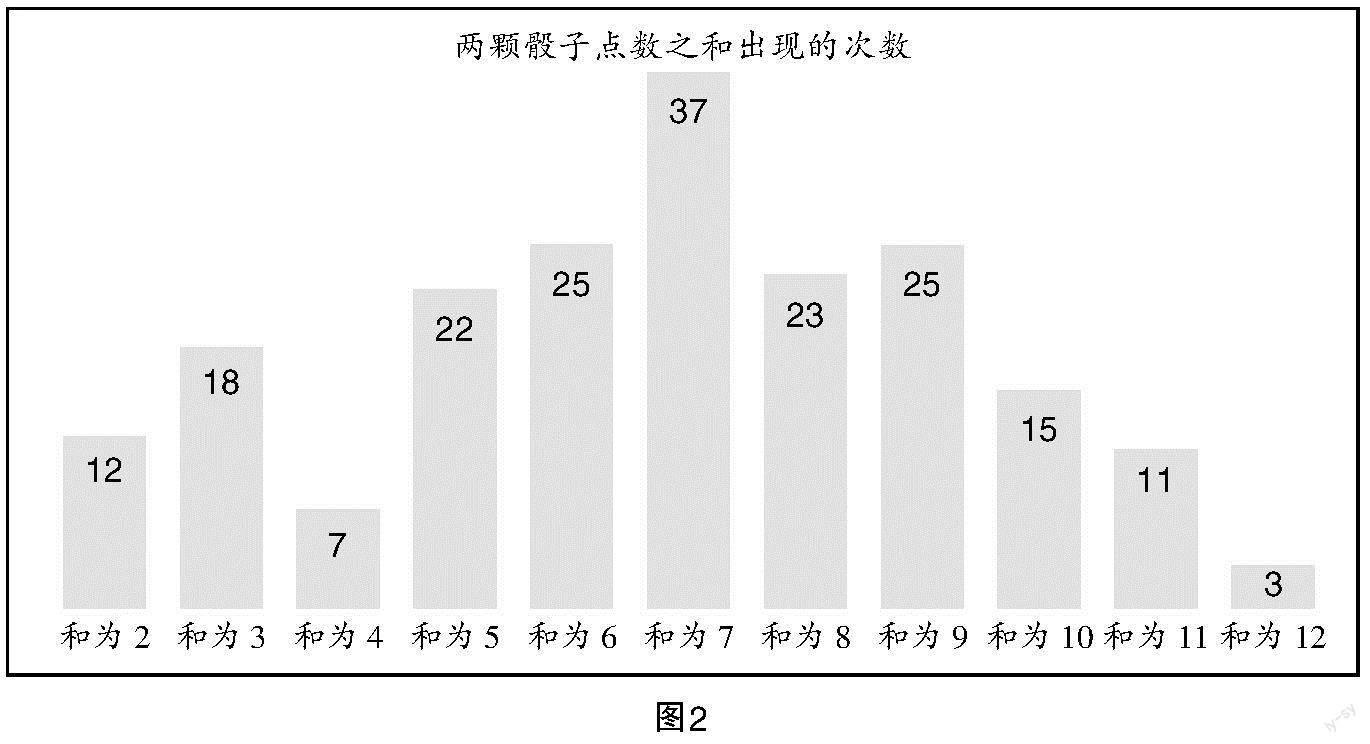
学生饶有兴趣地进行猜想，当学生充分表达自己的意见后，教师展示课前部分学生“抛骰子”的结果（见图2）.

教师提问：哪个结果出现的次数最多？学生一致回答“和为7”. 教师指出，按照初中所学知识可以认为，上述赌博游戏中，“点数和为7”的可能性最大.为什么会出现这种现象呢？学生带着问题进行学习和思考.

2. 小组合作，探究问题

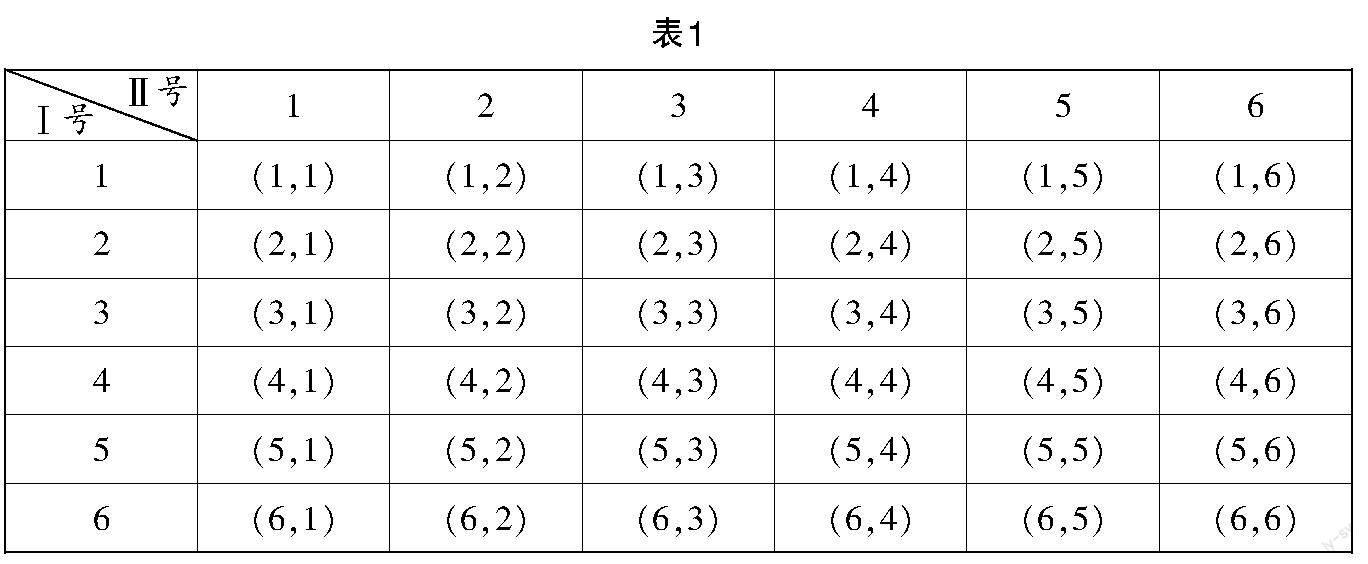
教师提示，研究事件出现的可能性，应该从该试验的样本空间着手，因为样本空间含有一个随机试验可能出现的所有结果.教师通过PPT展示“抛掷两颗骰子朝上点数”的样本空间（见表1）. 让学生根据样本空间合作探究：为什么“点数和为7”的可能性最大？

3. 整合观点，解决问题

经充分讨论，学生初步形成自己的观点：样本空间共有36个样本点，其中“点数和为7”的样本点有6个，比和为其他值的样本点的个数多，所以“点数和为7”的可能性最大.

教师充分肯定学生的发现，并追问：“同学们初步找到了分析随机事件发生的可能性大小的方法.在上述样本空间中，‘点数和为2’的样本点只有1个.而抛掷一枚质地均匀的硬币，观察其朝上一面的情况，发现这个试验的样本空间包括正、反两个样本点，其中‘正面朝上’的样本点也只有1个.请问：‘抛掷两颗质地均匀的骰子，朝上的点数和为2’的可能性与‘抛掷一枚质地均匀的硬币，正面朝上’的可能性相等吗？”“大家能借助路程与速度的关系对这一问题进行讨论吗？”

学生指出：路程相同并不代表速度相同，还要关注时间. 类似地，两个随机事件包含的样本点个数相同，不代表它们发生的可能性相同，还与样本空间中的样本点的总个数有关系.

教师追问：类比速度的计算方式，你能将随机事件发生的可能性用一个数值来表示吗？

学生思考后指出：用随机事件包含的样本点个数占样本空间包含的样本点总个数的比值表示随机事件发生的可能性大小.

教师充分肯定学生的创新思维、类比思维，让学生按照刚才的观点分别计算抛掷两颗质地均匀的骰子，朝上的点数和为2，3，…，12的可能性大小，并据此说明“点数和为7”的可能性最大的理由.

4. 数学抽象，模型初现

教师引导学生从上述具体事例中抽象出数学模型：一般地，事件A发生的可能性大小称为概率. 设随机试验E的样本空间Ω包含n个样本点，事件A包含其中的k个样本点，则

此处，教师不急于将该模型命名为“古典概型”，而将重点放在概率的计算方面，帮助学生初步理解该模型下概率的计算原理.教师举学生熟悉的例子以简单应用，如下所示：

人类白化病基因（a）是正常基因（A）的隐性，白化病是常染色体隐性遗传病. 一个家庭中父母双方均为正常，但因缺乏优生优育知识，不幸生育了一个白化病孩子. 请通过已知信息计算：父母双方再次生育一个健康孩子的概率.

5. 初步应用，模型完善

教师以常见的随机试验作为例题，学生借助上一环节所学知识计算随机事件发生的概率. 为创造完善的模型，例题应同时包含古典概型与非古典概型（主要指违背样本空间中的样本点的“有限性”和“等可能性”的概率模型）. 在解决问题的过程中，学生会发现上一环节抽象出来的模型有一些“漏洞”——当样本空间中的样本点不满足“有限性”或“等可能性”时，上一环节所得的模型“失灵”了，这可以引导学生注重模型的完善.例题如下：

例题1 从甲、乙、丙三人中任选两人担任课代表，甲被选中的概率为_____.

例题2 袋子中有5个大小质地完全相同的球，其中2个红球、3个黄球，从中不放回地依次随机摸出2个球，求下列事件发生的概率：

（1）A=“第一次摸到红球”；

（2）B=“第二次摸到红球”；

（3）AB=“两次都摸到红球”.

例题3 判断下面说法是否正确，并说明理由.

（1）某运动员连续进行两次飞碟射击练习，观察命中目标的情况，用y表示“命中”，用n表示“没有命中”，那么试验的样本空间Ω=｛yy，yn，ny，nn｝，因此运动员“两次射击都命中目标”的概率为0.25.

（2）从所有自然数中随机选取一个数字，这个数字小于10的概率是0.1.

6. 归纳总结，模型建立

教师指出：同学们刚刚归纳完善的模型正是古典概型. 同学们沿着数学家的足迹历经古典概型的建模过程，最终确定了这个模型，它能帮助我们解决生活中很多概率问题.

7. 知识贯通，模型应用

数学建模强调“应用性”，本环节借助完善后的古典概型解决不同领域的相关问题，进一步培养学生的数学建模素养.

练习1 从两名男生（记为B1和B2）、两名女生（记为G1和G2）中任意抽取两人.

（1）分别写出有放回简单随机抽样、不放回简单随机抽样和按性别等比例分层抽样的样本空间，并判断是否为古典概型.

（2）在上述三种抽样方式下，分别计算抽到的两人都是男生的概率.

练习2 “五行学说”是华夏民族创造的哲学思想，是华夏文明的重要组成部分. 古人认为，天下万物皆由金、木、水、火、土五类元素组成. 图3是金、木、水、火、土彼此之间存在的相生相克的关系图. 若从五类元素中任选两类元素，则两类元素相生的概率为_____.

总结反思

1. 遵循模型的生成规律

建模过程具备自身的规律. 建模的第一阶段包括发现问题、探究问题、解决问题三个环节，师生的主要任务是借助所学知识解决具体情境中的问题；建模的第二阶段包括模型初现、模型完善、模型建立三个环节，师生的主要任务是从具体情境中抽象出数学模型，并将模型“初步投入使用”，在应用中发现问题、完善模型；建模的第三阶段是模型应用环节，师生的主要任务是将建立的模型应用到不同学科领域，解决生活中的现实问题，从而巩固所学模型. 在第二阶段与第三阶段中应用模型的主要目的不同，第二阶段的目的是让学生在初步应用中检验和完善模型，第三阶段的目的是帮助学生巩固所学知识. 在当前部分建模教学中，经常忽略“模型初现”与“模型完善”两个环节，建模过程“一气呵成”后，立即进行大量练习. 这种形式确实可以快速推进知识学习，但不利于学生建模素养的培养.

在本课中，教师没有在具体情境中直接给出古典概型样本点的“有限性”和“等可能性”，而是引导学生将初步形成的带有“纰漏”的模型应用于解决更多问题.在问题解决中，学生会发现已有模型存在不足，产生对原模型进行完善的需求. 这种设计正是基于模型的生成规律，尽管建模过程充满了“曲折”，但学生正是从“完善模型”的过程中提升了数学建模的能力.

2. 注重学生的思维参与

数学建模过程有一个很重要的环节是情境探究，学生在探究过程中的思维参与程度直接影响了数学建模的效果. 因为只有学生深度思考具体情境中的关键问题，才能更好地实现从具体情境到数学知识的抽象. 这种从现实世界到数学世界的“飞跃”，正是数学建模的关键所在. 因此，教师应该在导入情境的设置上下功夫，选择生活中的真情境、历史中的典型情境、学生感兴趣的情境.同时，应该给学生留出足够的探究时间，让他们慢慢去“寻找”解决情境问题的数学知识.

在本课中，教师用历史情境“掷骰子”导入课题，以“两颗骰子朝上的点数和”的可能性大小设置问题，为更好地解决问题，让学生课前动手“抛骰子”试验，记录试验结果，发现“点数和为7”发生的可能性最大，这是学生第一次思维参与；为了深入探究“点数和为7”的可能性最大的原因，教师给出该试验的样本空间作为提示，学生合作探究后根据样本空间的情况指出“点数和为7”的可能性最大是由于样本空间中“点数和为7”的样本点最多，这是学生第二次思维参与；模型初现后，教师引导学生应用所学模型解决问题，在解决问题的过程中遇到样本点不满足“有限性”和“等可能性”的情境，学生带着疑问完善已有模型，最终得到古典概型的概念，这是学生第三次思维参与；最后，学生借助完善后的古典概型解决生活、文化等领域的概率问题，用数学知识解决实际问题，并在解决问题的过程中巩固知识、提升建模素养，这是学生第四次思维参与. 经历多次思维参与，学生更深刻地认识了古典概型.

3. 拓宽模型的应用领域

数学建模过程阐释了数学作为“工具性学科”的含义，但要让学生真正理解数学的“工具性”，需要跨学科、跨领域设置问题，因为只有学生能够体会到数学知识在生活和学科中有广泛应用，才能将数学作为解决问题的“工具”，在解決问题时“想到”用数学，“愿意”用数学.

在本课中，教师将古典概型与生物学中的遗传问题、现实生活中的抽样问题、传统文化中的“五行学说”等相结合，借助数学知识解决更多领域的概率问题. 由此学生能够深入领会数学模型的“广泛功能”，提高数学学习兴趣.

结语

数学建模素养是高中数学六大核心素养之一，培养学生的数学建模素养是数学教师的重要任务. 课堂是落实核心素养的“最后一公里”，因此课堂教学应当成为数学教师用心研究的一方天地. 在常态化教学中，遵循建模规律开展建模活动，注重学生的思维参与，并努力拓宽模型的应用领域，有利于更好地落实建模素养.

参考文献：

［1］ 王颖喆. 关于中学数学建模教与学的思考［J］. 数学通报，2020，59（11）：1-3+30.

［2］ 黄健，鲁小莉，王鸯雨，徐斌艳. 20世纪以来中国数学课程标准中数学建模内涵的发展［J］. 数学教育学报，2019，28（03）：18-23+41.

［3］ 蔡金法，徐斌艳. 也论数学核心素养及其构建［J］.全球教育展望，2016，45（11）：3-12.

［4］ 汪飞飞，张维忠. 中国中学数学建模研究的历程与论题及其启示［J］. 数学教育学报，2022，31（02）：63-68.