对合无穷远 斜率若比邻
吴昊





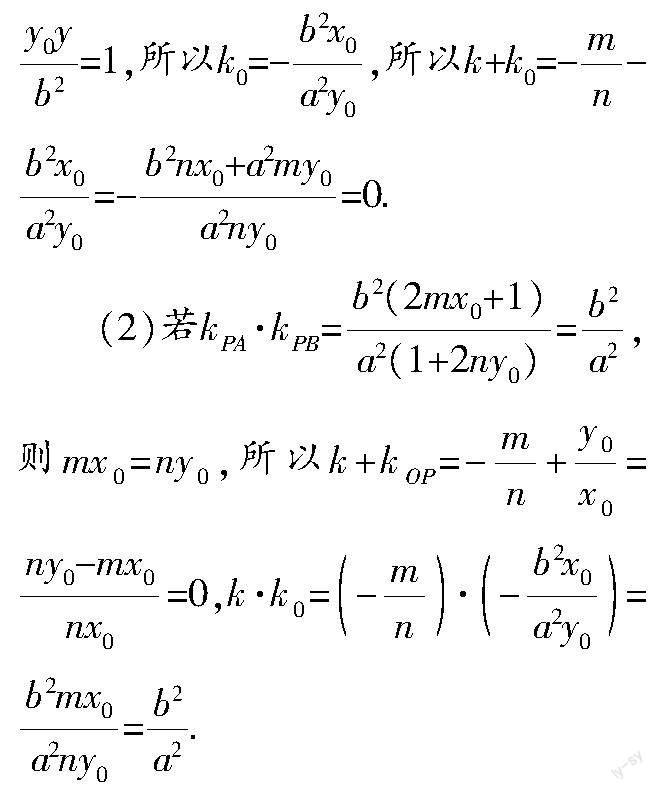



[摘 要] 文章对一道联考试题中的“多余”条件进行分析,探究一般性规律及其成因,得出与之相关的几个定理以及探究这些定理在解题中的应用.
[关键词] 斜率之和;斜率之积;对合;定值
笔者在做2023年“广州市一模”第21题时发现一个“直线过定点”的条件是“多余”的——其不影响结论的得出,这说明这类问题具有一般性的规律,于是笔者以此为出发点进行了一些探索,发现其背后的命题规律,愿与诸君分享.
缘溪行,仿佛有光
(1)求C的方程;
(2)直线l:y=k(x-1)(k≠0)与C相交于A,B两点,过C上的点P作x轴的平行线交线段AB于点Q,直线OP的斜率为k′(O为坐标原点),△APQ的面积为S,△BPQ的面积为S. 若AP·S=BP·S,判断k·k′是否为定值,并说明理由.
O,得到C′:(x+x)2+2(y+y)2=8,即x2+2xx+2y2+4yy=0.
疑惑:在解答过程中笔者发现,不用“直线l:y=k(x-1)(k≠0)过定点(1,0)”这个条件,依然能得出结论——斜率之积(k·k′)为定值,这是不是说明结论(斜率之积为定值)与已知直线是否过定点无关呢?一般情况下是否也有类似的结论呢?经进一步探索,笔者得到两个定理.
及点P处的切线的斜率都存在,分别为k,k,k,k.
综上可知,上述考题的第(2)问要证明的结论是定理1的结论(1),只是将条件k+k=0进行了包装.类比双曲线,又可以得到定理2(证明略).
得出这些结论后,笔者仍然在想,为什么会有这种简洁、对称的结论呢?
复前行,豁然开朗
如果将椭圆换成圆,用同样的方法可以得到定理3.
定理3 已知点P在圆C:x2+y2=r2上,直线l:y=kx+b(k≠0)与C相交于A,B两点,设直线PA,PB,OP及点P处的切线的斜率都存在,分别为k,k,k,k.
(1)若k+k=0,则k·k=1,k+k=0;
(2)若k·k=1,则k+k=0,k·k=1.
已知点P在C(圆或椭圆)上,直线l:y=kx+b(k≠0)与C相交于A,B两点,设直线PA,PB,OP及点P处的切线的斜率都存在,分别为k,k,k,k,则
(1)若k+k=0,则k+k=0,k·k=λ,
(2)若k·k=λ,则k·k=λ,k+k=0.
可以看出,若k+k=0,则总有k+k=0;若k·k=λ,则总有k·k=λ.而切线可以看成割线的极限,那么将圆内接三角形换成圆内接四边形,又能得到什么结论呢?
定理4 如图1所示,设圆内接四边形ABCD的边AB,BC,CD,DA所在直线的斜率都存在,分别为k,k,k,k,则
(1)若k+k=0,则k+k=0;
(2)若k·k=1,则k·k=1.
述,得证.
由此看来,对于圆内接四边形,若一组对边所在直线的斜率之和为0,则另一组对边所在直线的斜率之和必为0;若一组对边所在直线的斜率之积为1,则另一组对边所在直线的斜率之积必为1. 将四边形的其中一边缩小到一个点,即四边形变为三角形,用该点处的切線(斜率)代替该边所在直线(斜率),则为定理3. 类比到椭圆和双曲线,分别得到定理1和定理2. 从对合的角度来看,若P,A,B是二次曲线上的点,且PA,PB的斜率之和为0,则AB所过的定点无穷远,即直线AB的斜率为定值,其大小为点P处的切线斜率的相反数.
再回首,恍然大悟
以此为背景的考题为数不少,举两例如下:

