2023年全国乙卷文科第21题的解法与背景探究

秦文波 李超 李洁平

［摘  要］ 通过对2023年全国乙卷文科第21题（一道解析几何定点问题）的研究，得到了该题的5种求解方法，获得了2个推广结论，揭示了该类问题的命题背景和命题途径，丰富了该类问题的内容和解法.

［关键词］ 圆錐曲线；定点；极点极线；调和点列；命题背景；命题途径

数学运算是六大数学核心素养之一，是指在明晰运算对象的基础上，依据运算法则解决数学问题的素养.主要包括理解运算对象、掌握运算法则、探究运算思路、选择运算方法、设计运算程序、求得运算结果等. 从历年高考来看，解析几何是考查数学运算素养最佳的内容和载体，2023年也不例外. 其中，2023年全国乙卷文科第21题和理科第20题是相同试题，主要考查学生借助代数法研究椭圆几何性质的能力，以及化归与转化、数形结合等数学思想，以此检验学生的数学运算、逻辑推理等数学核心素养水平. 鉴于该题的典型性和示范性，为了提高复习备考效率，笔者从解法探究、拓展推广、命题背景等角度对该题展开了深入研究，现将研究结果呈现出来，以抛砖引玉.

试题呈现

（1）求C的方程；

（2）过点（-2，3）的直线交C于P，Q两点，直线AP，AQ与y轴的交点分别为M，N，证明：线段MN的中点为定点.

解法探究

思路1 设线，韦达定理，整体代换

解法1 （设线法1）若直线PQ的斜率不存在，则PQ与椭圆C只有一个交点，不符合题意，故直线PQ的斜率一定存在.设直线PQ的方程为y-3=k（x+2），P（x，y），Q（x，y）.

故线段MN的中点为定点（0，3）.

评注 由于整个几何运动系统可以看作由直线PQ绕点（-2，3）旋转引起的，因此选择设线法（设点斜式），即联立直线与曲线，得到关于x或y的方程，借助韦达定理求出两根和与两根积，将目标式整理成含两根和与两根积的形式后，利用整体代入法求解.

思路2 设线，齐次化联立

解法2 （设线法2）若直线PQ的斜率不存在，则PQ与椭圆C只有一个交点，不符合题意，故直线PQ的斜率一定存在. 设直线PQ的方程为y-3=k（x+2），P（x，y），Q（x，y），M（0，2t），N（0，2t），所以线段MN的中点的坐标为（0，t+t）.

故线段MN的中点为定点（0，3）.

评注 由于原问题可以转化为证明两直线斜率之和为定值的问题，故设线后通过齐次化联立能够巧妙求解. 值得注意的是，本解法蕴含着“平移”思想，若希望运算和书写

思路3 设点，整体构造

解法3 （设点法1）若直线PQ的斜率不存在，则直线PQ与椭圆C只有一个交点，不符合题意，故直线PQ的斜率一定存在. 设P（x-2，y），Q（x-2，y）.

背景探究

1. 类题探源

从历年高考试题来看，题1与下面的题2和题3是同源试题.

（1）求椭圆E的方程；

（2）过点P（-2，1）作斜率为k的直线与椭圆E交于不同的两点B，C，直线AB，AC分别与x轴交于点M，N，当MN=2时，求k的值.

2. 背景探析

通过研究笔者发现，上述3道试题都是以射影几何中的调和点列、调和线束、极点极线为背景命制的，其命题起点是调和线束的一个性质.

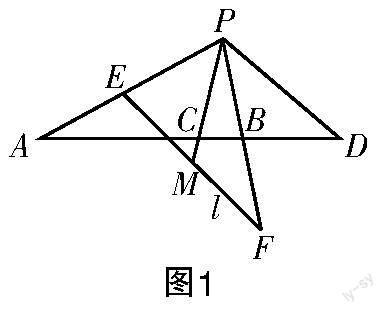
性质：平面内一条直线与调和线束中的其中一条平行而与其余三条相交，则相交线段被平分. 具体地，如图1所示，设直线PA，PB，PC，PD是一簇调和线束，直线l与直线PA，PB，PC分别交于点E，F，M，若l∥PD，则M为线段EF的中点.

拓展推广

结合上述性质，得到了下面的结论.

结论1 如图2所示，点T是椭圆C外一点，过点T作两条直线TA，TB分别与椭圆相切于点A和点B. 直线PQ经过点T且与椭圆C相交于P，Q两点，直线MN经过点B且与AP和AQ分别相交于点M和点N，直线AB与直线PQ相交于点E. 若AT∥MN，则B为线段MN的中点.

证明 由于TA，TB均为椭圆的切线，且A，B为切点，所以直线AB为点T对应的极线，T，E，P，Q为调和点列，射线AT，AE，AP，AQ是调和线束. 因为AT∥MN，根据上述性质，可得B一定为MN的中点.证毕.

进一步研究发现，结论1可以推广到双曲线、抛物线和圆等二次曲线中，又得到了下面的结论（证明与结论1类似，在此略去）.

结论2 已知点T是圆锥曲线Γ（圆、椭圆、双曲线、抛物线）外一点，过点T作两条直线TA，TB分别与圆锥曲线Γ相切于点A和点B. 直线PQ经过点T且与圆锥曲线Γ相交于P，Q两点，直线MN经过点B且与AP和AQ分别相交于点M和点N，直线AB与直线PQ相交于点E. 若AT∥MN，则B为线段MN的中点.

试题简解

1. 题1第（2）问简解

思路5 巧用极点极线

AT，AE，AP，AQ是调和线束. 又AT∥MN，故B为线段MN的中点，即线段MN的中点为定点（0，3）.

2. 题2第（2）问简解

研究展望