小图形、大智慧：数形结合思想在 小学数学解题中的应用

王凯

摘 要： 数形结合是小学数学学习中最为常见的一种思想.鉴于数学学科兼具“数”“形”双重特点，以及小学生的认知发展特点，将代数思想和几何思想有机融合起来，充分发挥图形的辅助价值，精准审题、理清数量关系、找到解题的“突破口”等，有效提升小学生的数学解题能力.本论文以此切入，结合一定的例题分析，对数形结合思想在小学数学解题中的具体应用进行了详细地探究，具备极强的参考价值.

关键词： 小学数学；数形结合；解题能力；课堂教学

“数”和“形”是数学学科的两大研究对象，且两者之间相互依存、不可分割.其中，抽象的数量关系，常常具备直观的几何意义；直观的几何性质，也需要借助精准的数量关系进行描述.因此，在数学学习中，唯有将“数”和“形”完美地结合到一起，才能实现深度学习.同时，数形结合还是一种非常重要的解题思想，在小学数学解题教学中，借助两者的有机融合，可帮助学生理清题目中的条件、数量关系等，极大地降低小学生的数学解题难度.

1  数形结合思想在小学数学解题中具体应用

1.1 数形结合，高效审题

审题是解题的关键.但是在具体审题中，由于部分题目中蕴含的条件十分复杂，而小学生的知识薄弱、理解能力薄弱，在审题的时候，常常面临诸多困惑，致使其审题不清，严重制约了小学生的数学解题.针对这一现状，唯有将数形结合思想融入到审题中，才能有效解决这一问题.

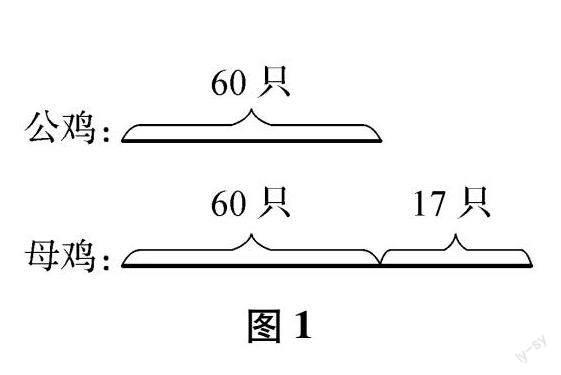
例1   在二年级数学“100以内的加法和减法”的应用题目中：李奶奶的养鸡场中，有公鸡60只，比母鸡少了17只，那么在李奶奶的养鸡场中，母鸡有多少只？

解析：  这原本是一道十分简单的应用题目，但是针对小学二年级的学生来说，在审题的时候，常常出现迷惑的现象，误认为“比母鸡少”就是减法.鉴于此，为了帮助学生真正理解题目的意思，就借助了数形结合的教学模式，结合题目画出线段图（如图1所示），使得小学生在直观的感知中，真正弄清题目的含义，并由此作出正确的答案，即：60+17=77（只）［1］.

例2    有两根长度相同的木材，第一根用去了1米，第二根用去了1.2米，第一根木材剩下的长度恰恰是第二根木材剩下的3倍.问：这根木材的长度是多少米？

解析：  在这一数学应用题解答中，学生常常阅读完之后，难以精准把握题目的条件，致使其因为审题不够全面深刻，导致解题方向出现偏差.鉴于此，在优化小学生审题时，就可融入数形结合思想，引导学生一边阅读一边画图，运用线段图将抽象的文字、数字进行转化，使其成为直观的图形.在这一题目中，可引导学生在审题时，以第二根木材剩余的数量作为参考标准，记为“1份”，那么第一根木材剩余的数量恰恰是3份，由此画出图形（如图2所示），并结合图形，得出：第一根木材比第二根木材剩余多出的2份长度，就是两份木材所用的长度差，即：1.2-1=0.2（米），因此，剩余1份的长度即为0.2÷2=0.1（米），因此，木材的总长度为1.2+0.1=1.3（米）.

1.2 數形结合，找准关键条件

在小学数学解题中，精准把握数学解题的条件，是进行解题的“突破口”.否则，一旦学生迷失在解题条件中，就会使其在解题中朝着错误的方向发展.鉴于此，在优化小学数学解题教学时，就可借助数形结合思想，将数学问题转化为直观的图形，以便于学生在形象的感知中，精准把握数学解题条件，形成明确的解题思路.

例3   有一桶油，经过两次使用之后，还剩余40升.已知，第一次用去了整桶油的 1 2 ，第二次用去了整桶油的30 % ，问：这桶油共有多少升？

解析：  在这一分数应用题解答中，学生经过审题之后，必须要精准把握题目中蕴含的已知条件，理清题目中已知条件的关系，才能在此基础上形成明确的解题方向.在这一题目中，解题的关键就是“经过两次使用之后剩余40升所对应的分数”，学生唯有明确40升在一桶油中占据的分数比例，才能找到解题的关键.此时，就可借助数形结合思想，指导学生结合题目画出对应的图形（如图3所示），接着结合图形分析，即可得出：1桶油即为单位“1”，第一次用去 1 2 ，即用去了单位“1”的50 % ，第二次用去了单位“1”的30 % ，由此得出单位“1”中还剩余20 % ，即40升.在此基础上，即可得出：40÷20 % =200（升）［2］.

例4   姐姐有10支铅笔，弟弟有4支铅笔，姐姐给弟弟几支铅笔之后，两个人的铅笔就一样多？

解析：  这是一道二年级的数学题目，但是在解题的时候频频出现错误.其主要原因就是没有找准解题的条件.结合小学二年级学生的认知特点，很难通过题目中的语言分析，找到解题的突破口.该题中，解题的关键就在于“给后两人一样多”.因此，在具体的教学中，就可先将图形画出来（如图4所示）.

指导学生结合线段图进行观察和思考：姐姐比弟弟多6支铅笔，如果全部给弟弟之后，就会导致弟弟比姐姐多6支铅笔，唯有将多出的部分平均分给两个人，才会一样多.至此学生即可结合图形，完成该题目的正确解答.

1.3 数形结合，明确数量关系

数量关系是学生正确解题的关键，尤其是在比较复杂的题目中，常常蕴含着多个数量关系，学生在分析问题的时候，常常出现分析不清、混淆关系等现象，致使其在解题的时候频频出现错误.鉴于此，就可充分借助相关的图形，引导学生在直观、形象化的图形工具中，将题目中的关系数量精准地展示出来，进而帮助学生形成明确的解题思路.

例5   甲乙丙三位同学都酷爱集邮.已知同学甲比同学乙多集了6张邮票，同学丙集的邮票是同学甲的2倍，比同学乙多集22张邮票，问：甲乙丙三位同学共集邮多少张？

解析：  这一题目中隐含着诸多数量关系，文字叙述也相对比较繁杂，思维薄弱的学生在解题的时候，常常出现无从下手的现象.鉴于此，在指导学生解题时，就可借助数形结合这一工具，先引导学生结合题目画出相关的图形（如图5所示）.

在图形的辅助下，并结合题目叙述即可分析得出：同学丙所集的邮票是同学甲的2倍，因此同学甲所集的邮票为：22-6=16（张）；同学丙所集的邮票为：16×2=32（张）；之后结合甲乙两位同学集邮的数量关系，即可得出同学乙所集的邮票为：16-6=10（张）.由此即可计算出三位同学一共集邮的数量.由此可见，在这一题目解答中，正是运用了数形结合的思想，将繁杂的数量关系直观地展示出来，帮助学生迅速理清题目中的数量关系，形成了正确的解题思路［3］.

例6   光明小学开展了第二课堂活动，已知书法小组中有30人，比合唱小组学生的人数2倍少6人，合唱小组有多少人？

解析：  这一题目的数量关系虽然比较简单，但学生在解题的时候，也常常出现错误，不少学生根据题目就直接得出：（30-6）÷2=12（人）.学生之所以会出现这种错误，主要原因就是解题的时候，没有弄清题目中的数量关系.鉴于此，就可融入数形结合思想，指导学生结合题目画出线段图（如图6所示）.

结合图形的辅助，学生即可轻松得知：书法小组的学生再加上6个人，恰恰是合唱小组的2倍.据此，即可结合正确的数量关系，得出正确的答案：（30+6）÷2=18.可见，通过数形结合思想的应用，可将抽象的数量关系直观地呈现出来，学生可以一目了然地精准解答出相关题目.

1.4 数形结合，开拓学生解题思维

在小学数学解题中，部分题目难度系数比较大，单纯地依靠题目很难形成明确的解题思路，致使学生面临着诸多困难.鉴于此，就可借助数形结合思想，将数字化进行图形化，赋予其数量意义，使得学生在直观的感知中，形成全新的解题视角，形成一定的解题思维.

例7   笼子中有20个头，54条腿，请问鸡和兔子各有多少只？

解析：  这是一道典型的鸡兔同笼问题，如果按照常规的思路进行解题，常常会陷入困境中.鉴于此，在引导学生进行解题时，就可借助数形结合的思想，引导学生结合题目中所给的条件绘制图形（如图7所示），先在图中绘制出20个头，接着再在每一个头上绘制出两条腿，结果发现还有14条腿，再在每一个头上加上两条腿，直到加完为止.如此，学生在图形的辅助下，即可形成明确的解题思路：假如笼子中全部为鸡，已知每一只鸡有2条腿，则拥有20×2=40（条）腿，还剩下54-40=14（条）腿，因为每只兔子4条腿，因此可将剩余的14条腿分给兔子，即14÷2=7（只），即可得出正确的答案.可见，在这一比较复杂的数学问题中，就是借助了数形结合思想，使得学生在图形的辅助下，形成了明确的解题思路［4］.

1.5 数形结合，避免常规性错误

小学生在数学解题的过程中，常常受到多种因素的制约，致使其出现各种各样的错误.导致这一错误的主要原因，就是学生在解题的时候，只是凭空想象，根本没有动手画图.鉴于此，在日常教学中，可引导学生灵活借助图形这一工具，帮助学生最大限度规避这些常规性的解题错误.

例8   小明家住在5层，他上3层走过的所有楼梯数为32级.那么，小明从1楼回到家，所要走多少级楼梯？

解析：  这是一道小学阶段最为常见的题目，也是小学生最容易出现错误的题目类型.多数学生在解这一问题的时候，常常认为3层对应的楼梯级数是32，那么每一层对应的楼梯级数为32÷3，小明回家要走5层，因此所走的楼梯级数为：32÷3×5，

尽管这一结果除不尽，但依然有很多学生选择了约等于.其实导致学生出现错误的主要原因是学生只读题目，没有画图，致使其不明确一层和二层之间有几个层级.鉴于此，就可引导学生先结合题目，画出简易的图形（如图8所示）.

如此，學生在直观的感知中，就会发现小明走到三层，实际上只走了两层楼梯，即：每一层楼梯的级数为：32÷2=16；而小明回家到5层，实际上所走的楼梯级数为32÷2×4=64.由此可见，在本题目解答中，学生只要结合题目，作出相关的图形，即可形成正确的认知，进而正确解答相关的问题［5］.

例9   现有一个长方形的卡纸，其长度为20厘米，宽为4厘米.根据需求，需要在这一长方形的卡纸上裁剪出若干个直角梯形，使得裁剪出来的直角梯形符合上底为3厘米、下底为5厘米、高为4厘米的标准.问：一共可以裁剪出多少个这样的直角梯形？

解析：  在对这一题目解答中，多数学生都是直接审题，并以面积作为切入点，迅速给出了具体的解题步骤：先将长方形、梯形的面积分别计算出来，即S 长方形=4×20=80（平方厘米）、S 直角梯形=（3+5）×4÷2=16（平方厘米），之后运用长方形的面积÷梯形的面积，即可得出5个.从逻辑上来说，这一解题模式不存在问题，但这一答案却是错误的，学生只要将相关的图形画出（如图9），就会发现：当剪出4个直角梯形之后，长方形卡纸中还剩下一个边长为4厘米的正方形，其面积虽然也是16平方厘米，与所要裁剪的直角梯形面积相同，但却无法将其裁剪出来.可见，在这一类型的数学题目中，并非是单纯依靠计算就能得到正确答案的，唯有借助图形的辅助才可.

2   基于数形结合思想的小学数学解题教学启示

经过课堂教学实践证明，数形结合是一种非常有效的解题工具，将其融入到日常解题训练中，使得原本复杂、抽象的数学问题，变得更加直观、形象，极大地降低了学生的解题难度.尤其是针对认知思维能力发展尚未成熟的小学生来说，小学数学教师在日常教学中，应结合实际情况，积极渗透数形结合思想，将其隐含到日常的数学概念、数学运算、数学应用题目的教学中，使得小学生在潜移默化的学习中，形成较强的数形结合意识；同时，鉴于数形结合思想的内涵，在日常教学中，还应培养小学生的画图能力，使其在解题和学习中，能够结合题目含义，迅速画出正确的图形［6］.

3 结束语

综上所述，数形结合是一种非常重要的学习工具，也是提升小学生数学解题能力的重要利器.鉴于此，小学数学一线教师在优化解题教学时，唯有彻底突破传统解题模式的束缚，适时植入数形结合思维，才能在以形助数、以数辅形的过程中，理清题目中的数量关系，找到解题的关键条件，形成明确的解题思路等，进而全面提升小学生的数学解题能力.

参考文献：

［1］ 廖加庆.数形结合在小学数学解题中的运用策略探究［J］.学苑教育，2022（25）：54 56.

［2］ 仇显吉. 小学高年级数学数形结合教学的重要性［C］.2022教育教学与管理南宁论坛论文集（一），2022：517 521.

［3］ 朱艳秋.数形巧结合，课堂更精彩——数形结合思想在小学数学教学中的运用与思考［J］.中国多媒体与网络教学学报（下旬刊），2021（12）：219 220.

［4］ 李标.数形结合的解题策略［J］.河南教育（教师教育），2021（8）：82 83.

［5］ 曹慧.数形结合思想让小学数学解题得心应手［J］.小学生（下旬刊），2021（5）：72.

［6］ 王生卓.研究数形结合思想在小学数学解题中的有效渗透［J］.教育界，2021（11）：60 61.