变式促进深度学习，探究提升思维品质

李荟

摘 要： 在整个初中数学知识体系中，二次函数线段问题是重中之重，也是考察的热点.但在传统教学中，学生针对这一部分知识学习依然停留在浅层阶段中，无法触摸知识的内核本质，学生只能解决简单的问题，一旦遇到较复杂的问题就无从下手.鉴于此，唯有基于变式训练，引导学生在一题多变中，完成知识的深度学习，才能真正提升学生的解题效率.本论文就以此作为研究的视角，结合一定的题目，针对二次函数中线段问题的变式训练进行了详细地探究，旨在提升学生的数学解题能力.

关键词： 初中数学；思维品质；二次函数；线段问题；变式训练

二次函数在教学中占据十分重要的地位，线段最值问题也是初中数学考察的热点.鉴于数学学科的特点，常常将两者结合到一起，进行综合性的考察.在传统初中数学课堂教学模式下，由于初中生学习到的知识点十分零散，并且学生自身思维能力发展有限，在面对二次函数中线段问题时，常常无从下手，无法形成明确的解题思路.鉴于此，初中数学教师在优化课堂教学时，唯有转变传统的解题教学模式，以具体的二次函数中线段问题作为例题，积极开展变式训练，促使学生在一题多变中，完成数学知识的深度理解、迁移和运用，真正提升学生的数学解题能力.另外，变式训练也是一种思维训练，极大地发展了学生的数学综合素养.

1 变式训练与数学解题教学

鉴于数学学科的特点，解题教学是初中数学教学的重要组成.现行数学教材上的题目，基本上都是对概念、公式、性质的直接运用，旨在借助相关的习题训练，帮助学生完成数学概念、数学公式、数学性质的理解.但是在考试的时候，题目更具综合性，涉及到的知识点更多， 对学生的要求更高.面对这一类型的题目，学生常常是无从下手，找不到具体的解题思路.导致这一现状的主要原因，就是數学教师在日常的解题教学中，常常“就题论题”，并未对题目进行阐发、引申和拓展，忽视了数学解题中的变式训练.

具体来说，变式训练就是立足于数学问题的实质，通过改变题目形式和条件，从不同的角度、不同层次将数学问题的本质暴露出来，进而促使学生在“一题多变”的训练中，深刻理解数学知识点，并促进数学知识的迁移和运用.同时，学生在变式训练的过程中，不仅加深了学习的深度，也在变式训练的探究和思考中，促进了数学思维的发展，真正提升了的数学综合能力，为学生更好地开展解题奠定了坚实的基础［1］.

2 二次函数中线段问题变式训练

在初中二次函数学习中，发现抛物线与直线相结合的题目常常处于压轴题的位置.但结合调查数据反馈发现，学生关于“二次函数中线段问题”的解答能力比较弱，在考试中频频出现失分现象.鉴于此，教师要积极开展变式训练，在“一题多变”的例题中，深化所学的知识点、促进数学思维发展，逐渐提升自身的数学解题能力［2］.

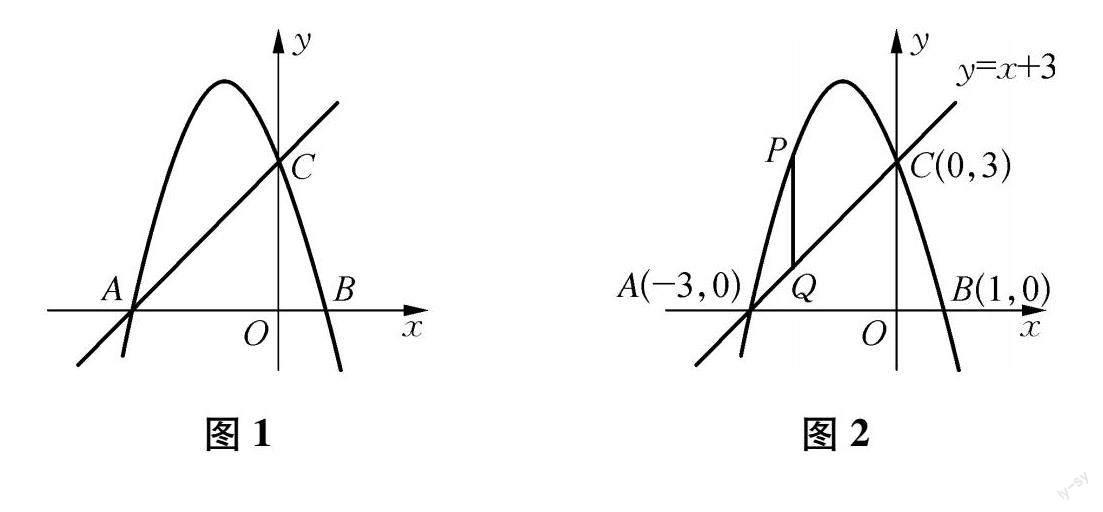
例1   如图1所示，已知二次函数y=-x2-2x+3的图象与x轴相交于A，B两点，其中A点在B点左侧，并与y轴相交于点C.

求：（1） A，B，C三点的坐标，以及直线AC的解析式.

（2） 如图2，点P是直线AC上方的抛物线上的一个动点，过点P做y轴的平行线，并与直线AC相交于点Q，求线段PQ的最大值.

解析：  针对题目（1），结合图象上A，B，C三点的位置，以及二次函数的解析式，即可轻松得出三点的坐标，这针对多数学生来说，均可轻松解答出答案.

题目（2），具备一定的难度.因为在这一题目中，将二次函数和直线结合到一起.在引导学生解答这一问题时，要指导学生在思考求线段PQ最大值的时候，先运用字母将P，Q点的坐标表示出来，假设P点的横坐标为m，则纵坐标为-m2-2m+3，得到P点坐标为P（m，-m2-2m+3），又因为PQ∥y轴，因此，点Q横坐标为m，则纵坐标为m+3.因此，Q（m，m+3）.得到Q点坐标为PQ的距离为（-m2-2m+3）-（m+3）=-m2-3m.

此时，就可将线段PQ的最大值转化为-m2-3m的最大值，学生可结合二次函数图象，对称轴等相关知识进行解答.

在完成基本的教学之后，为了帮助学生深刻了解这一部分知识，又以此为中心，对其进行了变式训练：

变式一：  如图3所示，点P是直线AC上方抛物线上的一个动点，过点P做x轴的平行线，与直线AC相交于M点，求线段PM的最大值.

解析：  在变式一中，所求问题为“线段PM的最大值”，但是在具体求解时，由于P、M两点仅有纵坐标相等，不易确定横坐标，致使无法直接解答这一题目.此时，就可借助转化的思维，引导学生对线段PM进行转化.而要达到这一目标，就可过点P做PQ∥y轴，与直线AC相交于Q点.如此，就构建出了△PQM.由于PQ∥y轴，因此∠PQM=∠OCA.因为PM∥x轴，因此∠PMQ=∠CAO.结合A、C两点的坐标，可判断出△OAC为等腰直角三角形，即∠CAO=∠OCA=45 ° .因此，在△PQM中，∠PQM=∠PMQ=45 ° .因此，该三角形也为等腰直角三角形，即PM=PQ.此时，就可将线段PM的最大值转化为线段PQ的最大值.之后，学生便可按照原题的解题思路，顺利完成这一题目的解答.

变式二：  如图4所示，点P是直线AC上方的抛物线上的一个动点，求点P到直线AC距离的最大值.

解析：  变式二比变式一更深一层，难度更大.在解答这一问题时，可引导学生结合题目和图象分析，明确要想得出点P到直线AC的距离的最大值，就必须要过点P做直线AC的垂线，即PH⊥AC.此时，就将所求问题转化为线段PH最大值.

在具体求解的过程中，由于线段PH最大值难以确定，必须要再次进行转化，过点P做PQ∥y轴.由于△PQH为等腰直角三角形，因此，PH=  2  2 PQ.

此时，要想求出线段PH最大值，只需要求线段PQ最大值.之后，即可根据原题目的解题思路进行求解.

变式三：  点P是直线AC上方抛物线上的一个动点，过点P做PQ∥y轴，并AC相交于Q点，过点P做PH⊥AC，求△PQH的周长.

解析：  在这一变式训练中，可参考图4进行观察分析，得△PQH周长为PQ+QH+PH，结合变式二，得△PQH为等腰三角形，PH=QH=  2  2 PQ.因此，求△PQH周长最大值时，就可将其转化为求线段PQ的最大值，又回归到原题的解题思路中.

变式四：  如图5所示，点P是直线AC上方抛物线上的一个动点，连接PA，PC，求△PAC面积的最大值.

解析：   在变式四训练中，要想求出△PAC的面积，就可借助“割补”的方式进行，鉴于本题目，可直接思考“割”法进行求解：过点P做PQ∥y轴（如图6所示）.此时，就可将△PAC的面积最大值进行转化成S △PAC=S △PAQ+S △PCQ= 1 2 PQ·AO= 3 2 PQ.如此，经过转化之后，△PAC的面积最大值即可转化为线段PQ的最大值，学生利用原题解题思路即可完成.

变式五：  如图7所示，点P是直线AC上方抛物线上的一个动点，连接PB与AC相交于F点，求 PF BF 的最大值.

解析：  这一变式训练难度逐渐增加，学生要想求 PF BF 的最大值，必须要结合这两条线段构建相关的图形，结合初中阶段学生所学的知识，应引导学生将其与相似三角形知识结合到一起.于是，过点P做PQ∥y轴，与直线AC相交于Q点；过点B做BH∥y轴，与直线AC相交于H点.此时，可结合相似三角形性质，将 PF BF 进行转化，使其变成： PF BF = PQ BH = 1 4 PQ.因此，这一题目又转化为求线段PQ的最大值.

经过五次变式训练之后，就会发现无论是三角形的周长，还是三角形的面积，亦或是相似三角形对应边的比例关系，都可以通过转化，最终成为竖直线段的最大值.因此，在日常二次函数中最值问题求解中，必须要引导学生学会运用转化思想，将其进行转化，最终成为二次函数中垂直线段的最值问题，以便于学生轻松解答［3］.

例2：  已知抛物线y=2x2-12x+16，该抛物线与x轴相交于A，B两点，与y轴相交于C点，顶点为D.点P是抛物线对称轴上的一个动点，要使得△PAC周长最小，求P点的坐标.

解析：  如图8所示，连接BC，与直线x=3相交于P点，根据对称轴的性质，得出PA=PB，鉴于此，可得知直线BC的解析式为y=-4x+16，由此得出P的坐标为（3，4）.可以说，在解答这一问题时，关键就是找出A点关于x=3的对称点，并结合“两点之间线段最短”的性质进行解答.

为了帮助学生对本节内容形成深刻的理解，就对其进行了以下变式训练：

变式一：  抛物线y=2x2-12x+16，该抛物线与x轴相交于A，B两点，与y轴相交于C点，顶点为D.在该抛物线上有一点E，其横坐标为5，点F（m，0）是x轴上的一个点，当FC+EF值最小时，求m的值.

解析：  如图9所示，这一变式题目相对比较简单，要想使得FC+EF值处于最小时，应关于对称轴做E点的对称点E′，连接CE′，使其与x轴相交于F点.由此，结合已知条件，可的求得CE′直线的解析式为y=- 22 5 x+16，因此，F  40 11 ，0 .随即，结合“两点之间线段最短”的性质，得出：FC+EF=FC+E′F=CE′，由此得出：m= 40 11 .

变式二：  抛物线y=2x2-12x+16，该抛物线与x轴相交于A，B两点，与y轴相交于C点，顶点为D.点G（0，n）是y轴上的一个动点，求线段GD与GA中较长的线段减去较短线段差的最小值和最大值，并求出n的值.

解析：  如图10所示，结合题目含义，以及图象观察，当A，G，D三点共线的时候，|GD-GA|=AD，据此可得出直线AD的解析式为y=-2x+4，此时可简单求出G点的坐标为（0，4），因此，n=4.当G′D-G′A=0的时候，可得出G′D=G′A，因此，|GD-GA|存在最小值，为0.此时，AD的垂直平分线G′E的解析式应为y= 1 2 x- 9 4 ，进而求出G′点的坐标为 0，- 9 4  ，因此，n=- 9 4 .

变式三：  抛物线y=2x2-12x+16，该抛物线与x轴相交于A，B两点，与y轴相交于C点，顶点为D.K是OC中点.Q是一动点，从K点出发，经过x轴上的M点，再经过对称轴上的N点，然后返回到C点.如果动点Q所走的路程最短，请据此找出M，N点的位置，并求出最短的路程.

解析：  如图11所示，结合抛物线对称轴的性质，可找出K点，C点的对称点，分别为K′，C′，将其连接，与x轴相交于M点，与直线x=3相交于N点.由此即可确定出动点Q经过的最短路程S=KM+MN+CN=K′M+MN+C′N′=K′C′.之后结合已知条件，可由C和K点的坐标， 推出C′和K′点坐标，即C′（6，16），K′（0，-8），最终计算出最短的路程S=6 17 .

在例2以及三个变式训练中，难度有所增加，不仅涉及到的数学知识比较多，也融入了数学模型的认知.学生经过原题和变式训练的分析，经历了化繁为简、化难为易的深度思考，不仅掌握了二次函数中线段最值的相关知识，也在深度思考和探究中，促进了思维的发展［4］.

3  初中数学解题教学中变式训练注意事项

变式训练核心就是围绕某一核心知识点，引导学生在不断的变式训练中，对知识的发生、发展过程形成深刻的感知，使其在理解知识的基础上，促进知识的迁移和应用，使其在深度思考中，学会举一反三、触类旁通，真正提升初中生的数学解题能力.鉴于此，为了日常解题教学中，更好地开展变式训练，应注意以下三个问题：

第一，变式训练应具备适用性.初中数学教师在开展数学变式训练之前，必须要了解学生的实际能力、已有知识掌握情况，设计出与学生学习需求相契合的变式训练题目，力求通过变式训练促使所有学生的发展.同时，在设计变式训练题目时，还应设定多种难度，以免变式题目过于简单，导致师生“白忙活一场”，收效却不大.

第二，变式训练应具备针对性.为了提升数学解题变式训练的有效性，在设计变式训练时，必须要把握知识点的本质，通过适当的改变，进而为学生提供多个解题思路，使得学生在多角度思考和解题中，真正掌握这一核心知识点，并促进知识的迁移.

第三，变式训练应渗透数学思想.变式训练就是在本质特征不变的情况下，对问题情形、思维的角度进行改变.其中蕴含着大量的数学思想，如：数形结合、转化思想等.这就要求在具体的解题变式训练中，应科学、适时融入数学思想，使得学生在使用数学思想分析解答题目的过程中，促进思维的深度发展，循序渐进提升自身的解题能力［5］.

4 结束语

综上所述，变式训练有助于帮助学生深刻理解知识的本质，实现知识的迁移和灵活运用.同时，变式训练还是打开学生数学思维的“钥匙”，是促进高阶思维发展、提升数学核心素养的关键，更是提升学生数学解题能力的必然选择.因此，初中数学教师在开展解题教学时，必须要积极开展变式训练，引导学生在“一题多变”的训练中，获得提升和发展.

参考文献：

［1］ 罗文武.顺向连接 逆向对称——二次函数中线段“和”最小问题［J］.数理化解题研究，2019（14）：2 3.

［2］ 蔡定宏，杜懿.二次函数的应用之线段最值问题［J］.中学数学教学参考，2021（2）：52 55.

［3］ 施长燕.变式促進深度学习，探究提升思维品质——以二次函数中线段问题为例［J］.数学学习与研究，2022（14）：62 64.

［4］ 徐葵，杨文.浅析初中数学线段最值问题解题策略——以二次函数为例［J］.理科爱好者（教育教学），2021（3）：27 30.

［5］ 马娇，钟鸣.深度教学：整体设计、系统演绎、变式训练——以“二次函数的几何应用”为例［J］.数学之友，2018（8）：33 35.