“双减”背景下小学数学课堂核心问题设计的现状及干预策略研究

黄伟东

摘 要： 为响应国家“双减”政策号召，笔者结合省数学学科教学基本要求，调查研究小学数学课堂核心问题设计现状，并进行归因分析，从路径探索、策略实施两方面阐述对小学数学课堂核心问题设计的干预，以求学生在减负不减质中深度思考，提升数学思维.

关键词： 核心问题；现状归因；设计路径；有效策略

南京大学郑毓信教授指出，“微观意义上的核心问题”是指就一节课或相关的几节课提炼出相应的“核心问题”.“宏观意义上的核心问题”能通过整体性分析弄清内在脉络，并凸显其中的关键，从而真正起到提纲挈领的作用.

本文关注的课堂核心问题是指教师基于对教材的深度理解和对学情的精准把握，在课堂上精心设计适合学生探究的、提升学生高阶思维的问题.核心问题一般具有一定张力和弹性的特点，能使学生的学习聚焦并主动探究、层层深入.

1  研究背景及现状

1.1  减负提质增效率：响应国家双减政策的号召

2021年7月，中共中央办公厅、国务院办公厅印发了《关于进一步减轻义务教育阶段学生作业负担和校外培训负担的意见》，其中提出“优化教学方式，提升课堂教学质量”“提高学生学习效率，促进学生全面发展”等意见.该文件的发布为“提高教师核心问题设计能力”的提出奠定了基调，从国家层面锚定了战略高度.

1.2  赋能促思蕴素养：落实省市学科教学的要求

2021年9月印发的《浙江省小学数学学科教学基本要求（2021版）》中第8条指出：“教学环节的构建和情境的创设都须注重数学问题的设计.问题的有效设计是推进课堂教学进程的关键.”结合××市教科研院发布的教科研指导意见，笔者进行了小学数学核心问题设计的研究，为构建素养课堂，从省市层面笃定了研究方向.

1.3  区域调研显问题：聚焦核心问题设计的困惑

笔者通过对区域内103位教师进行调查问卷，聚焦小学数学课堂核心问题设计的现状并尝试归因，发现教师存在以下困惑：

1.3.1 问题缺乏深度，无法立足知识本源

教材的认知是问题筛选的前提，但调查中53.4 % 的教师提问时过多关注教学内容，缺乏对教材的深入解读和对核心问题的提炼.

1.3.2 问题缺乏力度，无法依托学习路径

活动的开展是问题联结的载体，但调查中69.9 % 的教师在教学时不擅长基于学习路径以问题链助推问题的解决.

1.3.3 问题缺乏梯度，无法彰显弹性分层

素材的选取是问题发生的支架，但调查中87.4 % 的教师不擅长提供多元素材驱动自主建构，难以满足不同学生的探究需求.

1.3.4 问题缺乏广度，无法渗透数学思想

思维的发展是核心问题设计的导向，但调查中32.0%的教师的问题设计缺乏思维空间，无法融入数学思想.因此，笔者希望在小学数学课堂核心问题设计的路径及策略上干预，以期提高教师核心问题的设计能力，并在课堂教学实践中发展学生的数学核心素养.

2  小学数学课堂核心问题设计的基本路径

基于小学数学课堂核心问题的现状调查及归因分析，笔者查阅资料并结合自身教学经验尝试以逻辑起点、基本依据、形成过程以及网状体系为路径展开设计小学数学课堂核心问题（如图1）.

2.1  确立核心问题设计的逻辑起点

核心问题设计的逻辑起点包括结构性的数学内部和关联性的数学外部.数学外部包括学生已有知识经验、认知结构以及不同年龄阶段的学生的心理特点等，数学内部则包括数学教材中的上位知识、显性知识以及隐性知识.

2.2  明晰核心问题设计的基本依据

问题是课堂的核心，是启发和引导学生探究的有效载体，但教师的问题往往过于直接，问题与问题之间的跨度比较小，限制了学生的数学思考.因此，笔者以发展学生的数学思维为依据来设计核心问题，以存在逻辑关系的问题链启发学生在师生互动的过程中提出本原性问题，从而将教材、教师以及学生的问题整合为课堂学习的核心问题.利用核心问题的牵引力以及问题链的驱动力，提高教师课堂教学的有效力.

2.3  形成核心问题设计的有效过程

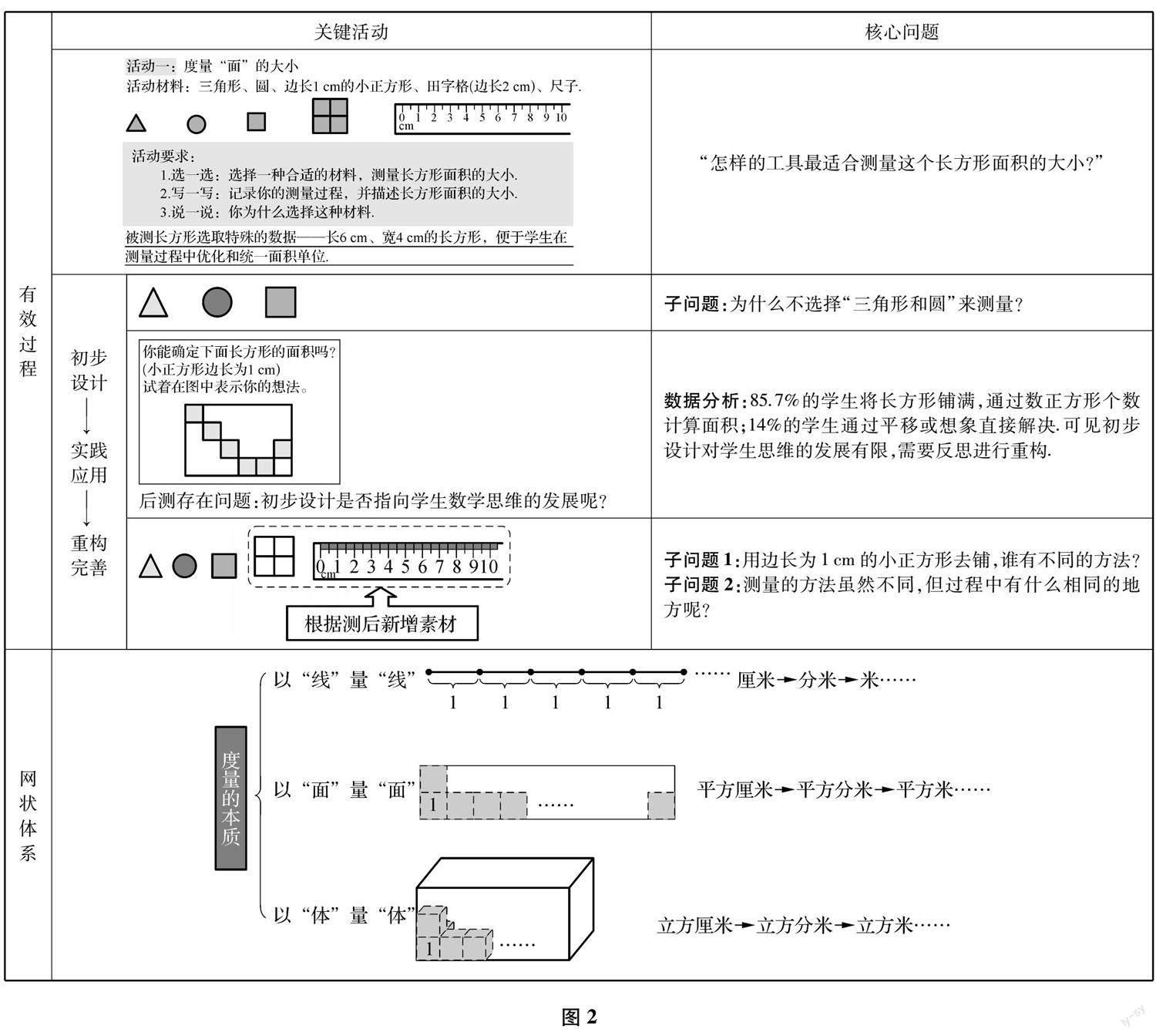
核心问题设计的有效过程通常需要经历“初步设计——实践应用——重构完善”三个過程（如图2）.确定核心问题后，在不断的实践反馈与跟踪调整中，对活动材料进行重构完善，新增“田字格”和“尺子”，旨在扩充核心问题的思维空间，使学生经历从“田字型”到“日字型”再到“口字型”的逐步调整过程，积累将“大单位”细分为“小单位”的活动经验，从而理解统一单位的必要性.由于学生的认知水平存在差异性，为了让不同思维层次的学生在同一教学环境中获得最高效的收获，唯有依托核心问题的引领，以多元素材的选择，实践学为中心的教育本真.

2.4  建构核心问题设计的网状体系

有效的课堂核心问题并不只是针对单一一节课的设计，而应对同类型的其他教学内容的核心问题设计也有启发性和可操作性.比如前文中提到的以“面”量“面”的数学内容，笔者在设计核心问题时都会与之前学习的以“线”量“线”以及后续的以“体”量“体”教学联系起来，其设计核心问题的路径也是一脉相承的.笔者以一节课核心问题的有效设计关联一类课，做好连点成线、织线成网，结网成体（如图2）.

3  小学数学课堂核心问题设计的有效策略

3.1  以教材结构为本，单元视角整合核心问题

案例1   从《三角形》单元整体角度确立核心问题总方向、总思路及总框架.

3.1.1 整体解读教材，明晰核心问题总方向

四年级学生对平面图形的认识经验已较为丰富，也形成了一定的图形探究能力，尤其是四年级上册（人教版）中角和四边形的学习，给学生积累了学习三角形的活动经验，学生能将学习四边形的学习经验迁移到三角形的认识中.因此，本单元的学习适合整合，通过对教材的整体解读，确定以“边”和“角”两大元素整合教学内容，明晰核心问题的总方向.

3.1.2 整体创设单元，形成核心问题总框架

单元视角下，笔者尝试创设《三角形》单元整体教学结构，并形成各部分应有的课堂核心问题总框架以及相应的子问题.比如在“边”的教学中，利用三根小棒的拼摆活动分别解决：① 搭一个三角形需要几根小棒？② 三根小棒一定能拼成三角形吗？③ 符合条件的三根小棒能摆出不同形状的三角形吗？④ 选择不同长度的小棒搭不同类的三角形.这四个目标指向明晰的子问题，从而完成对三角形“定义——关系——特性——分类”的整体认识，丰富概念的内涵和外延.

3.1.3 整体把控学情，理清核心问题总思路

在充分研读教材的基础上，对学生的学情进行把控，得到学生对该单元知识的困惑以及已有的经验水平，并及时进行精准的分析和理解，从而确定核心问题的总思路.教师只有了解学生在三角形认识过程中的思维障碍点和知识生长点，才能对症下药地设计有层次、有弹性、有思维空间的核心问题，统筹安排教学任务，开展有针对性的学习活动，让学生的思维能力发展都落在最近发展区中.

3.2  以重难关键为点，深度关联形成问题链条

小学数学课堂教学应在教学的重、难关键之处设计核心问题.教师应根据教学目标对核心问题进行分解，创設有梯度、有关联的子问题，并以核心问题的牵引力激发问题链的驱动力，盘活学生已有的认知力，导引学生后续的学习力，建构结构化的知识网.

3.3  以活动素材为支，多元拓宽培养提问意识

核心问题的落实离不开活动素材的设置，单一的素材容易让学生走向“程序员”的操作误区，不利于学生的思维发展.因此，教师要精心设计多元的活动素材，引导学生的思维不断碰撞，鼓励学生发现和提出问题.

案例2   《圆锥的体积》差异比较.

单一的活动素材和多元活动素材的课堂教学片段如图3所示，以求凸显活动素材多元化的重要性.虽然都以活动素材为支架进行操作实验，得出结论，但［方案一］仅提供等底等高的圆锥与圆柱，限制了学生思维的发散， 而［方案二］避免了学生忙于操作实验而淡化思考和分析的现象，促使学生在多元素材的对比沟通中主动寻求共性规律，揭开表象，深究其内在联系.

3.4  以数学思想为引，迁移延展深化核心素养

在教材迁移之处设计核心问题，有助于改变教师自身散点状、割裂式的思维方式，养成一种强调方法更强调思想的内在迁移式的思考习惯.而学生对新旧知识的充分联结、迁移和延展能让其数学核心素养达成深化.

案例3   《商是两位数的除法》教学以核心问题推进进程.

以核心问题“612÷18竖式有几层”推进教学进程，以“第一层分什么？”“第二层分什么？”“商是几位数，写在什么位上？”三个子问题盘活学生已有的认知力，导引学生后续的学习力，让学生将“位值的概念”和“竖式的层数”有效地联系起来，结构化地理解除法竖式的模型，实现学生思维从低阶向高阶的发展，从而实现“一层竖式”向“二层竖式”的思维进阶，“二层竖式”向“多层竖式”的思维迭代过程（如图4）.

“双减”是一项政策，更是一种行动，我们响应“双减”号召，以学科教学基本要求为引，共聚“核心问题设计”研究，思考路径，探究策略，减中有增，增中有提，为减负，为提质，更为共进.让我们致力于教与学现状的改善，以学生终身成长为目标，让教育返璞归真，让“双减”落地生根.

参考文献：

［1］ 郑毓信.中国数学教育的“问题特色”［J］.数学教育学报，2018，27（1）：1 7.

［2］ 刘媛.“核心问题”引领下的小学数学课堂教学策略研究［D］.南京师范大学：2020.