对边简支十次对称二维准晶板弯曲问题的辛分析

范俊杰, 李联和, 阿拉坦仓

(1. 内蒙古师范大学 数学科学学院, 呼和浩特 010022;2. 内蒙古自治区应用数学中心, 呼和浩特 010022;3. 无穷维哈密顿系统及其算法应用教育部重点实验室, 呼和浩特 010022)

0 引 言

自Shechtman等[1]在1984年首次发现准晶体之后,人们对准晶的电子结构、光学、磁性、热和弹性理论进行了大量研究[2]．准晶体是具有准周期原子排列和旋转对称性的新的固体结构．准晶中有两种不同类型的低频元激发,即声子场和相位子场．

近年来,一些定量描述和分析准晶弹性理论的数学方法也得到了很大发展,并取得了一系列有价值的结果．Fan[3]和他的团队发展了经典弹性理论中的消元法,将复杂的准晶弹性方程简化为一个或几个高阶偏微分方程,然后通过Fourier变换法或复变函数法求解．此外,广义摄动方法[4]、Green函数方法[5]、积分变换法[6]、复变函数法[7-8]、半逆解法[9]、势理论方法[10]和Stroh形式法[11]也成功地被推广和应用到准晶弹性理论问题的研究中．

辛方法由钟万勰[12]在20世纪90年代提出,用于求解弹性板和梁等问题．该方法的主要特点是求解过程在具有对偶变量的辛空间中进行,而不是在具有一种变量的Euclid空间中进行．在Hamilton系统的框架内,可以通过变量分离和辛特征函数展开的方法获得所考虑问题的精确解,而无需对解形式进行任何先验假设,这显示了辛方法的独特优势．辛方法理论基础是无穷维Hamilton算子特征函数系的完备性,Alatancang等[13-14]在该领域取得了一些成果．目前,辛方法已应用于各种研究领域,如弹性[15-18]、黏弹性[19-20]、纳米力学[21-22]、断裂力学[23]、压电[24-25]、功能梯度效应[26]、波传播[27]等．Zhou等[28]研究了有限尺寸一维六方压电准晶双材料中V形界面缺口的Ⅲ型断裂行为．Yang等[29]分析了具有复杂结构的压电石英晶体的Ⅲ型断裂行为．Wang等[30-31]研究了二维准晶的平面弹性问题．Qiao等[32]将辛方法推广到八次对称二维准晶的平面弹性问题．

本文首次研究了十次对称二维准晶中厚板问题的辛方法及其数学理论基础．通过引入适当的状态函数,将十次对称二维准晶中厚板弹性的位移平衡方程转化为一组由一阶常微分方程组成的Hamilton对偶方程,并给出了相应Hamilton算子矩阵的特征值．基于辛特征函数系的完备性定理,得到了给定边界条件下二维十次对称准晶中厚板弯曲问题弹性场的解析表达式,并与已有结论进行了比较．

1 十次对称二维准晶板弯曲问题的基本方程

假设z方向为十次对称二维准晶周期方向,xoy平面是准周期平面．对于十次对称二维准晶,由准晶弹性理论[3],有变形的几何方程

(1)

不考虑体力情况下的平衡方程

(2)

广义Hooke定律

(3)

其中C66=(C11-C12)/2;σij(σij=σji),εij(εij=εji),ui和Cij分别是声子场的应力、应变、位移和弹性常数;Hij(Hij≠Hji),wij(wij≠wji),wi和Ki是相位子场的应力、应变、位移和弹性常数;R是声子场和相位子场的耦合弹性常数．这里记(x,y,z)=(x1,x2,x3)．

基于Mindlin板理论,关于十次对称二维准晶板弯曲问题假设如下[33]：

(4)

其中uz(x,y)为中面挠度,φx(x,y),φy(x,y)和vx(x,y),vy(x,y)分别是声子场和相位子场中xoz与yoz平面内的转角．

将式(4)代入式(1)中,得到

(5)

弯矩Mxx,Myy和Mxy, 剪力Qx和Qy,广义弯矩Nxx,Nyy,Nxy和Nyx可以表示为

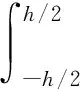
(6)

其中h是板的厚度．

将式(3)和(5)代入式(6),得到弯矩、广义弯矩和剪力的表达式为

其中τ=h3/12．

十次对称二维准晶板的力和力矩平衡方程可以表示为

(7)

其中q是板在单位面积上的横向荷载．

2 十次对称二维准晶板弯曲问题的Hamilton对偶方程

引入状态函数

(8)

则由式(7)和(8)可得到Hamilton正则方程为

(9)

这里H为Hamilton算子,且

(10)

Z=(uz,φ1,φx,vx,φ2,Qy,φy,φ3,φ4,vy)T,

f=(0,0,0,0,0,-q,0,0,0,0)T．

下面将采用辛方法求解对边简支矩形十次对称二维准晶中厚板问题,板的坐标和尺寸如图1所示．此问题的边界条件可以表示为

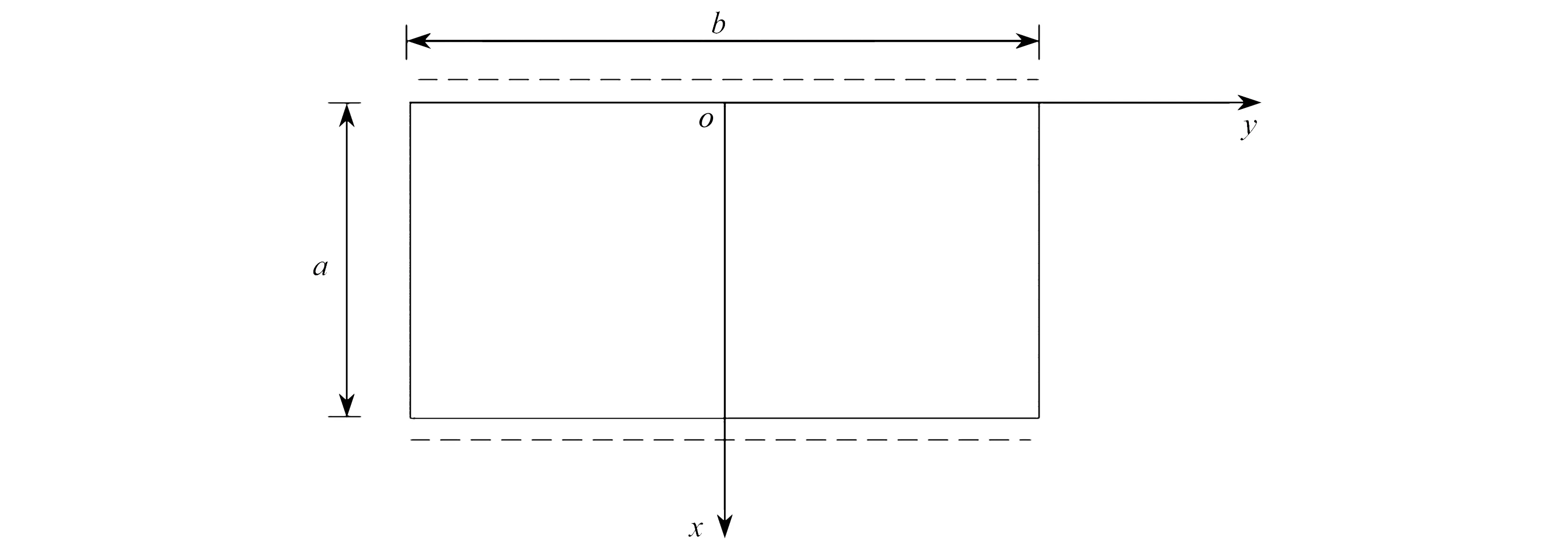
图1 矩形准晶中厚板示意图Fig. 1 Schematic diagram of a rectangular quasicrystal medium thickness plate

uz(x)|x=0,a=0,φy(x)|x=0,a=0,Mx(x)|x=0,a=0,vy(x)|x=0,a=0,Nxx(x)|x=0,a=0．

(11)

3 十次对称二维准晶板弯曲问题的辛分析

式(8)对应的齐次Hamilton方程为

(12)

设Z=X(x)Y(y),并将其代入式(12),得到

(13)

HX(x)=μX(x),

(14)

其中,μ是Hamilton算子矩阵H的特征值,

X(x)=[uz(x),φ1(x),φx(x),vx(x),φ2(x),Qy(x),φy(x),φ3(x),φ4(x),vy(x)]T

(15)

是满足边界条件(11)的特征向量．

由式(14)求得Hamilton算子矩阵H的特征多项式为

(16)

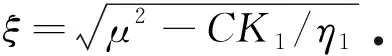
Xi(x)=(Ai+Bix+Cix2+Dix3)cos(μx)+

(Ei+Fix+Gix2+Hix3)sin(μx)+Sicos(ξx)+Risin(ξx),

(17)

其中Ai,Bi,Ci,Di,Ei,Fi,Gi,Hi,Si和Ri(i=1,2,…,10)是待定常数．将式(17)代入式(14)中可以得到常数之间的关系．

3.1 Hamilton算子H的特征值和特征向量

将式(17)代入边界条件(11),为使式(17)存在非零解,令对应的系数行列式为零得

sin4(aξ)sin(aξ)=0,

(18)

进而可得

(19)

(20)

式(19)是四重根,式(20)是单根．

将式(19)代入式(14)可得μn,μ-n相应的特征函数为

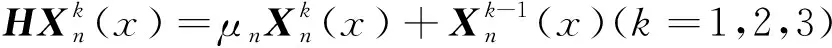
3.2 特征函数系的辛正交性和完备性

下面讨论Hamilton算子H的特征函数系的辛正交性,给出了特征函数的展开系数,并讨论了特征函数系的完备性．

我们用X表示Hilbert空间L2(0,a)×L2(0,a)×L2(0,a)×L2(0,a)×L2(0,a)×L2(0,a)×L2(0,a)×L2(0,a)×L2(0,a)×L2(0,a)．

定义1 算子的所有特征向量和Jordan形式特征函数的集合

(21)

为广义特征函数系．

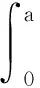
〈U(x),U(x)〉=0, 〈U(x),V(x)〉=-〈V(x),U(x)〉．

引理1 由定义1给出的广义特征函数系满足如下辛正交关系：

其中

定理1 在Cauchy主值意义下,Hamilton算子的特征函数系(21)在Hilbert空间X中是完备的．

证明对于∀F=[f1(x),f2(x),f3(x),f4(x),f5(x),f6(x),f7(x),f8(x),f9(x),f10(x)]T∈X,在Cauchy主值意义下由广义特征函数系(21)给出的辛-Fourier展开式为

(22)

根据引理1,可知

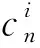
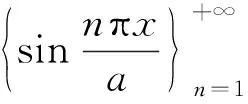
3.3 十次对称二维准晶板弯曲的辛解析解

由定理1和解的叠加原理,式(9)的通解可以表示为

(23)

式(9)中向量f=(0,0,0,0,0,-q,0,0,0,0)T可以表示为

(24)

其中

其余系数全为零．

将式(23)和式(24)代入式(9)得到微分方程组

(25)

解微分方程组(25)得

(26)

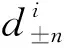
(27)

挠度uz(x,y)的解析表达式为

(28)

其中

弯矩Myy,Mxx和广义弯矩Nxx,Nyy的解析解表达式为

(29)

(30)

(31)

(32)

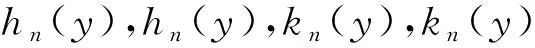
当不考虑相位子场时,式(28)和式(29)与文献[34]中经典板的解完全相同．

4 数 值 结 果

为讨论所提出方法的有效性,本节给出了十次对称二维准晶板在不同长宽比下的挠度uz(qa4K1/η2)在中点处(a/2,0)的数值解,其中材料参数为[33]

C11=23.43 GPa,C12=5.741 GPa,K1=12.2 GPa,K2=2.4 GPa,R=-0.11 GPa．

如表1所示,本文获得的级数解具有较好的收敛性．

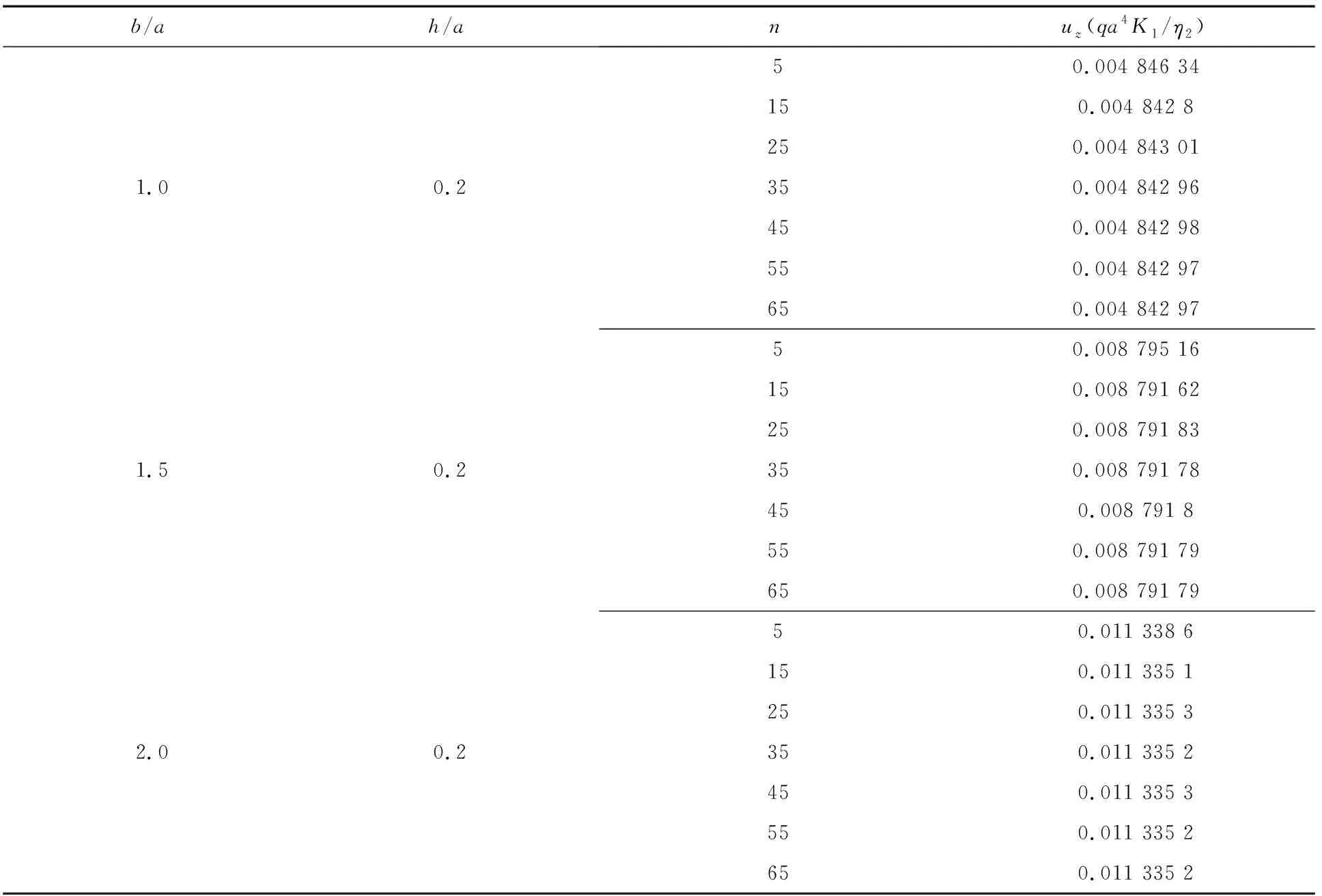
表1 不同宽度和厚度比下中点处的挠度

5 结 论

本文将辛方法应用于十次对称二维准晶中厚板弯曲的问题研究,通过引入适当的对偶变量,将问题表述为Hamilton正则系统．证明了相应Hamilton算子矩阵的广义特征函数系统在Cauchy主值意义下具有辛正交性和完备性,保证了Hamilton系统分离变量的可行性,并导出了精确解析解．随后,对解析解进行了退化比较研究,并给出数值结果,以证明解析解的收敛性和准确性．本文方法的优点在于不需要提前假设任何函数,方法直观合理,为解决准晶板的弹性问题提供了一种系统的方法．此外,该方法有望应用于准晶板的屈曲和振动等问题的研究中．

致谢本文作者衷心感谢内蒙古师范大学基本科研业务费(2022JBZD010;2022JBXC013)、内蒙古农业大学基础学科科研启动基金项目(JC2020002)和内蒙古师范大学研究生科研创新基金项目(CXJJB22011)对本文的资助．

附 录 A

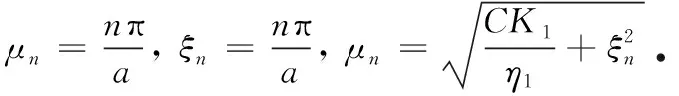
附 录 B

其中n=±1,±2,…．

附 录 C

附 录 D

hn(y)=e-yμn(C11K1ebμn/2(-2+e(b+2y)μn(b-2y)μn+2yμn-e2yμn(b+2y)μn+

η2(2-bμn)+ebμn(-2+2yμn+η2(2+bμn)))+4(R2+C12k1)eyμn(1+ebμn)2-

e3bμn/2+2yμn(2R2(2+bμn-2yμn)+C12K1(4+bμn-2yμn))+

e(b+4y)μn/2(2R2(-2+bμn-2yμn)+C12K1(-4+bμn-2yμn))+

ebμn/2(2R2(-2yμn+η2(-2+bμn))-C12K1(2+2yμn+η2(2-bμn)))-

e3bμn/2(2R2(2yμn+η2(2+bμn))+C12K1(2+2yμn+η2(2+bμn)))),

η2(2-bμn)+ebμn(-2+2yμn+η2(2+bμn)))+4(C11K1-R2)eyμn(1+ebμn)2-

e3bμn/2+2yμn(C11K1(4+bμn-2yμn)-2R2(2+bμn-2yμn))+

e(b+4y)μn/2(2R2(2-bμn+2yμn)+C11K1(-4+bμn-2yμn))+

ebμn/2(2R2(2yμn-η2(-2+bμn))-C11K1(2+2yμn+η2(2-bμn)))-

e3bμn/2(C11K1(2+2yμn+η2(2+bμn))-2R2(2yμn+η2(2+bμn)))),