网络化Euler-Lagrange系统的分布式编队机动控制

杨吉康, 于晋伟, 杨卫华

(太原理工大学 数学学院, 太原 030600)

0 引 言

近年来,随着机器人控制技术的日益成熟,机器人已应用于更加广泛的领域,特别是一些危险的或者其他一些特殊场合,满足矿井作业、水下测绘、桥梁探伤、火星探险等应用需求．然而,无论单个机器人的功能和效用如何提高,单机器人自身性能毕竟有限,特别是对于复杂的工作任务及多变的工作环境,其能力尤显不足．与单个机器人相比,多机器人系统具有更大的灵活性以及更高的可靠性,能够完成更复杂的任务．例如,在军事领域中,通过多机协同可以控制多架低成本无人机实施蜂群作战,进而大幅度提高其突防能力、毁伤能力以及作战效费比,达到“1+1≥2”的效果．然而,随着控制系统规模的越来越大,也产生了更为复杂的控制问题,如多机路径规划问题[1]、子系统避碰问题等[2]．为了解决这些问题,多机器人的自主协同控制技术应运而生[3-7]．怎样充分发挥多机器人系统的优势,解决其系统中存在的问题并降低不利影响,使系统能够在复杂环境中更高效地完成任务,是目前多机器人系统研究的目标．

网络环境下多智能体系统协同作为一种新的多机器人应用形式,近年来引起了国内外学者的广泛关注与研究兴趣,无论是在理论上还是应用上都取得了丰硕的研究成果[8-13]．其中由Euler-Lagrange动力学所描述的网络化机器人系统的协调控制已成为十分活跃的研究课题之一．这是由于经典的Euler-Lagrange方程可以有效地描述各种机械系统,包括机械手、步行机器人、飞行航天器等,而这种网络化机械系统的协同具有更高的可操作性、可靠性、可扩展性以及灵活性．因此,对于网络化Euler-Lagrange系统的深层次理论研究具有十分重要的科学意义和应用前景．最近的代表性研究工作有：文献[8]研究了有向网络拓扑下具有通信时延的不确定机械系统的一致性问题;文献[9]研究了基于事件触发的Euler-Lagrange多智能体系统分布式最优一致性问题;文献[10]研究了多Euler-Lagrange系统的领航跟随一致性问题;文献[11]研究了网络化Euler-Lagrange系统的采样一致性问题;文献[12]研究了未知Euler-Lagrange系统跟踪期望时变轨迹的鲁棒跟踪控制问题等．值得注意的是,目前大部分关于Euler-Lagrange系统编队控制的研究都是控制多个智能体形成期望的编队构型,并在向目标运动的过程中维持特定的几何构型,未考虑编队机动过程中的构型控制情况．编队机动控制的任务通常是在给定整体机动参数后,使编队的质心、方向、尺度等几何参数连续变化,考虑到多智能体编队控制中时变编队信息会影响控制器的设计以及系统的分析,因而用于时不变编队形状控制的方法不能简单地推广到时变编队机动控制的研究中．显然,面向实际工程技术领域中,考虑机动控制的网络化Euler-Lagrange系统能够更好地适应实际的需求．

在编队机动控制相关的研究工作中,通常都是采用领航-跟随法．其中领航者决定时变的机动参数,跟随者在其控制算法下形成期望队形．为了形成时变的期望队形,现有的方法大致分为两类： ① 每个智能体可以访问机动参数; ② 只有领航组能够访问机动参数．当每个智能体都能访问编队机动参数时,编队机动控制就变成了共识追踪问题,其中智能体协作保持一个时变编队[14-17]．某些应用场景中,编队中的智能体可能具有不同的智能级别,只有领航者才能感知和响应动态环境,也就是说,只有领航者才能够访问随时间变化的部分或者全部机动参数．在这种情况下,可以为每个跟随者设计估计器来获得编队机动参数．然而,控制器的性能会受到估计误差的影响,估计量也会消耗计算和通信资源．为了避免使用估计器,另一种方法是考虑编队中智能体之间某些不变约束,如相对距离、相对方位[18]．在以相对距离为约束时,编队中的智能体能够在自己的局部坐标系中感知其邻居的相对位置,然后控制其达到目标编队,这表明智能体不需要有局部坐标系的公共方向,也就是说,基于距离的编队机动控制可以实现旋转和平移机动,而无需为跟随者设计估计器来估计只有领航者知道的时变机动参数．类似地,可以通过基于相对方位的方法实现缩放和移动操作．

最近提出了一些无估计器的方法,如基于重心坐标的控制方法[19-21]、基于应力矩阵的控制方法[22-30]和基于复杂Laplace算子的控制方法[30-31]．然而,现有的无估计器方法还存在着一些局限性：第一,文献[19-20,25,28-31]的工作只能应用于低阶多智能体系统;第二,基于复Laplace的方法仅仅适用于二维空间;第三,文献[20-30]中的方法需要凸的或者通用标称结构,即任意3个标称编队中的智能体不在同一条直线上,任意4个标称编队中的智能体不在同一个平面上;第四,文献[20,26-28]没有对领航者的控制器进行设计,这限制了编队的机动性,文献[26]中编队机动控制的追踪误差只能收敛到有界紧集,文献[32]中的工作需要智能体的相对运动状态,但在高阶多智能体系统中测量相对速度和相对加速度是不切实际的．

本文受上述理论研究以及工程应用价值的激励,研究了网络化Euler-Lagrange系统的分布式半全局反馈编队机动控制的问题．主要创新表现在如下四点：第一,相比于大部分关于Euler-Lagrange系统编队控制的研究都是控制多个智能体形成期望的编队构型,并在向目标运动的过程中维持特定几何构型,本文研究的是编队机动控制,要求智能体不仅能够形成期望的编队构型,并且在给定整体的机动参数后编队的质心、方向、尺度等几何参数可以实现连续变化．第二,相比于文献[25],本文研究的是应用更为广泛的强非线性Lagrange系统,低阶线性多智能体系统的控制方法已不适用．第三,所提出的编队机动方法在全局坐标系未知的情况下,不仅适用于一般或者凸标称结构,而且适用于非一般和非凸标称结构．第四,结合滑模控制理论,构造了完全分布式的机动控制协议,编队系统中跟随者无需知道编队时变机动参数就可以实现期望任务．

本文的其余部分组织如下：第1节描述了一些预备知识和问题陈述;第2节给出了不确定网络化Euler-Lagrange系统的编队问题的主要结果;第3节给出了相应的模拟结果;最后第4节给出了结论．

1 预备知识和问题陈述

1.1 符号说明与图论知识

‖·‖2为给定向量和矩阵的2-范数,In×n表示n×n单位矩阵,设1n为n中的全一向量,设0为全零矩阵或向量,⊗为Kronecker积,定义D∈SO(n)表示一个n维旋转矩阵的集合．考虑在p维空间中由n个智能体形成的编队,其表示为qi∈p,i=1,2,…,n．设G={V,E}为有n个非空点的集合V={1,2,…,n}和有向边集合E⊆V×V构成的具有网络拓扑的有向图．Ni≜{j∈V： (j,i)∈E}表示智能体i的邻居点集合．如果(j,i)∈E,则表示智能体i可以获取智能体j的信息．(G,q)表示由智能体qi∈p,i=1,2,…,n形成的编队．

1.2 网络化Euler-Lagrange系统动力学

假设编队网络由n个Euler-Lagrange系统组成．第i个系统的动力学方程简写为[4]

(1)

其中,qi∈p是广义坐标向量,Mi(qi)∈p×p是对称正定的惯量矩阵,p×p是Coriolis离心力矩阵,gi(qi)∈p是重力向量,τi∈p是控制输入．控制系统(1)有如下3个重要的基本性质[33-37]．

性质1 存在4个正常数a>0,b>0,c>0,d>0,对于任意的x,y以及z∈p,都有

a≤‖Mi(qi)‖2≤b, ‖gi(qi)‖2≤c, ‖Ci(x,y)z‖2≤d‖y‖2‖z‖2．

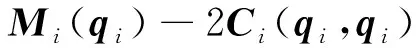
性质3 对于任意的x,y∈p,系统(1)可线性参数化为

(2)

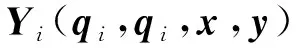
1.3 问题陈述

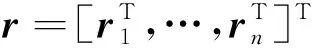
(3)

式(3)等价于

(4)

通过矩阵理论我们可以知道要求构造智能体相对约束的最少智能体个数：

ωijeij+ωikeik=0;

(5)

ωijeij+ωikeik+ωiheih=0．

(6)

我们可以将式(6)中参数ωij,ωik,ωih写成向量形式：

(ωij,ωik,ωih)(eij,eik,eih)T=0．

(7)

同样地,式(5)也可以写成这种形式,对于每一个智能体i,i∈Vf,通过式(3),跟随组的一组距离约束可以写成如下的矩阵形式：

(Ωf⊗I2)r=0,

(8)

其中Ωf∈nf×n定义为跟随矩阵,满足

(9)

注1 由跟随矩阵的定义可知,其可以不是方阵,并且不要求对称,这与文献[22]中定义的应力矩阵不同．该文献中要求矩阵是方阵且为对称矩阵,即ωij=ωji．并且,传统Laplace矩阵中的权重一般是非负的,但是跟随矩阵中的元素可以是负数．

由于智能体被划分为领航者和跟随者,故跟随矩阵可以写为如下形式：

Ωf=[Ωfl,Ωff],

(10)

其中Ωfl∈nf×nl,Ωff∈nf×nf．据此,式(8)等价于

(Ωfl⊗I2)rl+(Ωff⊗I2)rf=0．

(11)

定义1[22]若rf可以被rl确定,即Ωff是非奇异的,则称标称编队(G,r)为可局部化的．

也就是说,如果(G,r)为可局部化的,则标称编队中跟随组的标称位置可以由领航组的标称位置表出

(12)

接下来,通过一个例子来说明如何计算一个标称编队的跟随矩阵Ωf中的子矩阵Ωfl以及Ωff．考虑在二维平面中由7个智能体组成的系统,如图1所示．其中有3个领航者：ri=[4,0]T,rj=[2,2]T,rk=[2,-2]T,4个跟随者：rh=[0,2]T,rm=[0,-2]T,rp=[-2,2]T,rq=[-2,-2]T．图中有向箭头表示智能体信息传递的方向．

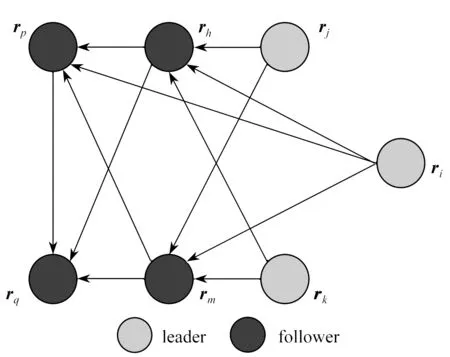
图1 标称队形Fig. 1 The nominal formation

由式(3),通过计算可得智能体h与智能体i,j,k的距离约束为

-2ehi+3ehj+ehk=0．

(13)

同理,智能体m与智能体i,j,k的距离约束为

-2emi+emj+3emk=0．

(14)

智能体p与智能体i,h,m的距离约束为

-2epi+5eph+epm=0．

(15)

智能体q与智能体h,m,p的距离约束为

-eqh+eqm+eqp=0．

(16)

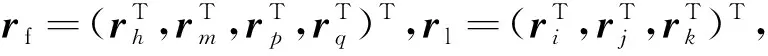
(17)

其中

(18)

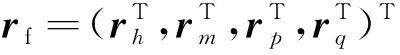
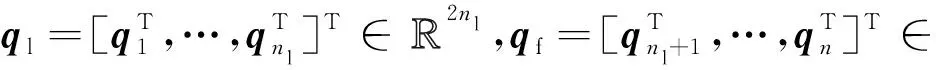
q*(t)=a(t)[In⊗Q(t)]g(t)+1n⊗b(t),

(19)

其中a(t)∈,Q(t)∈SO(2),b(t)∈2分别为时变缩放、旋转和平移编队机动;为时变编队队形,类似于式(11)中的标称编队,g(t)应满足

(Ωfl⊗I2)gl(t)+(Ωff⊗I2)gf(t)=0．

(20)

式(20)中的Ωfl和Ωff是由式(7)中所示的标称编队(G,r)计算出来的．

注2 如果不需要改变队形,则有g(t)=r,其中r为标称构型．那么式(19)中所期望的时变编队为

q*(t)=a(t)[In⊗Q(t)]r+1n⊗b(t)．

(21)

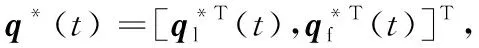
(22)

这表明,跟随者可以实现期望的时变编队形状缩放机动、旋转机动和平移机动．而不需要估计只有领航者知道的时变机动参数g(t),a(t),Q(t),b(t)．本文的目标是设计一个特定的控制率,使得所有的跟随者都能达到跟随者和运动的领航者之间的速度匹配,同时系统仍能够实现时变机动编队．定义2进一步解释了本文的编队机动控制问题．

定义2 在有向网络拓扑结构下,如若下面等式成立,则称控制协议τi能够解决网络化Euler-Lagrange系统的编队机动控制问题．智能体i的状态满足

2 网络化Euler-Lagrange系统的控制器设计

本节讨论了网络化不确定性Euler-Lagrange系统中领航者和跟随者的编队控制问题．目标是为系统设计合适的控制协议,以便实现时变期望机动编队．首先对系统中的领航者设计控制器,实现领航者的机动编队;其次对系统中的跟随者设计控制器,要求设计出来的控制器可以实现跟随者在无需获取只有领航者知道的时变机动参数的情况下可以跟随领航者运动．

为了设计控制器,引入以下假设．

假设2 跟随者可以接收3个智能体信息．

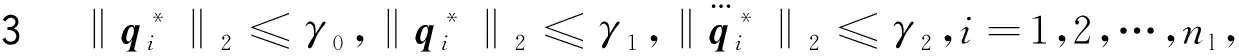
注4 由假设1可知,编队的运动状态包括缩放、旋转和平移．根据编队需求,可以分别对不同时变机动参数进行设置．在1.3小节中,通过对跟随矩阵的定义(式(9))以及网络拓扑的设计,要求每个跟随者能够在与相邻智能体相对距离参数的约束式(3)下实现期望的时变机动编队,而不用估计或者知道时变机动参数．这意味着在二维平面中,跟随者需要接收3个相邻智能体信息．即假设2成立是对编队网络拓扑结构的要求．由于考虑到多智能体在实际控制过程中,它们的期望速度、期望加速度以及期望加速度的导数往往都是有界的．因此提出了假设3．

2.1 领航者编队控制器设计

定义3 在有向网络拓扑结构下,如若下面等式成立,则称控制协议τi能够解决网络化Euler-Lagrange系统中领航者的编队机动控制问题,智能体的状态满足

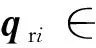
(23)

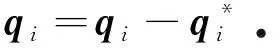
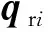
(24)

利用式(23)给出的参考速度,为第i个智能体设计如下的滑模：

(25)

式(25)可以进一步写为

(26)

将编队控制协议设计为

(27)

所期望的自适应变化率选择为

(28)

其中ki,Λi都是正定对称矩阵．

通过将式(27)代入到式(1)中,闭环系统(1)可以被写为

(29)

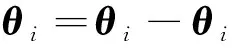
定理1 在假设1—3下,利用控制算法(27)和自适应律(28),网络化Euler-Lagrange系统中领航者能够在定义3意义下实现期望的队形：

证明考虑下面的Lyapunov函数：

(30)

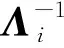
对Vi求导,同时利用式(28)、式(29)和性质2,可得

(31)

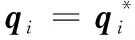
2.2 跟随者编队控制器设计

定义4 在有向网络拓扑结构下,如若下面的等式成立,则称控制协议τi能够解决网络化Euler-Lagrange系统中跟随者的编队机动控制问题．智能体的状态满足

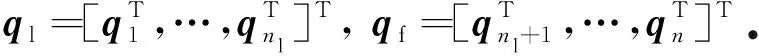
注6 易知,定义2等价于定义3和定义4．

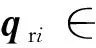
(32)

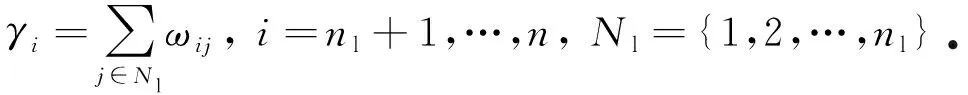
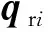
(33)

利用式(32)给出的参考速度,为第i个智能体设计如下的滑模：

(34)

那么式(34)可以被写为

(35)

将编队控制协议设计为

(36)

所期望的自适应变化率选择为

(37)

其中ki,Λi都是正定对称矩阵．

通过将式(35)代入到式(1)中,闭环系统(1)可以被写为

(38)

通过运用跟随矩阵(9),由式(35)可知,跟随组的滑模可以写为

(39)

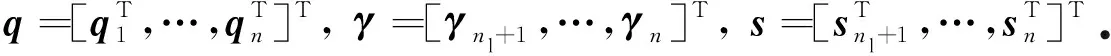
进一步地,跟随组的滑模可以被写为

(40)

定理2 在假设1—3下,利用控制算法(27)、(36)和自适应率(28)、(37),网络化Euler-Lagrange系统能够在定义3、定义4意义下实现期望的队形：

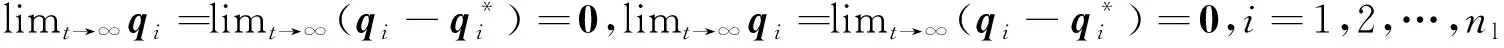
考虑下面的Lyapunov函数：

(41)

其中i=nl+1,…,n．利用式(37)和(38)以及性质2,对Vi求导,有

(42)

注7 定理1和定理2在给出了有向图拓扑结构下,网络化Euler-Lagrange系统实现编队机动控制的充分条件．

注8 定理1和定理2的证明表明,所提控制算法仅使用了滑模控制方法就可以实现对网络化Euler-Lagrange系统的编队机动控制,所得结果不要求凸标称队形,比基于应力矩阵理论得到的跟踪控制算法有一定的优越性[19]．

3 仿 真 实 验

为验证所设计控制算法和编队理论的正确性和有效性,本节给出例子进行数值仿真．在仿真中模拟一个复杂的环境．在这个环境中,智能体需要通过两个隧道以实现避障．因此,智能体编队需要改变编队的形状、方向和位移．在仿真中只有领航者才能够感应和响应环境,以证明所提控制策略的有效性．假设第i个智能体的动力学方程如下[34]：

(43)

其中

M11=a1+2a3cos(qiy)+2a4sin(qiy),M12=M21=a2+a3cos(qiy)+a4sin(qiy),M22=a2,

仿真中实际使用的参数为a1=3.3,a2=0.97,a3=1.04,a4=0.6．回归矩阵Yi的元素为

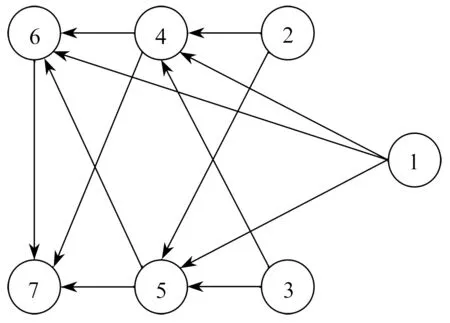
图2 通信图Fig. 2 The communication diagram

由式(7)、(9)、(10),计算可得跟随矩阵Ωf以及子矩阵Ωfl和Ωff：

(44)

(45)

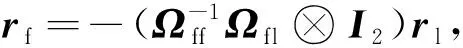
(Ωfl⊗I2)gl(t)+(Ωff⊗I2)gf(t)=0,

(46)

其中Ωfl和Ωff在式(45)中给出．

领航者的编队队形gl(t)设计为

gl(t)=(4 0 2 2 2 -2)T．

(47)

结合式(46)和(47),可得跟随者的时变队形为

(48)

期望队形为

(49)

gl(t)=(154 -30 156 -30 157.7 -30)T．

(50)

结合式(46)和(50),可得跟随者的时变队形为

(158.85 -30 160.55 -30 161.7 -30 163.4 -30)T．

(51)

期望队形为

(52)

为了更加直观地验证控制算法和编队理论的有效性,仿真中给出了系统在控制算法(27)和(36)下,系统随时间的状态变化．图3给出了7个系统在160 s内的输出轨迹,并给出了部分时刻系统的输出分布．图4给出了系统在Ox轴和Oy轴方向上的追踪位置误差,图5给出了系统在Ox轴和Oy轴方向上的追踪速度误差,图6给出了系统中控制器的状态,图7给出了不同时刻系统中自适应参数的更新状态．从图3、图4可以看出7个系统能够实现编队机动控制并且达成一致状态．从图5可以看出7个系统的速度误差最终能够收敛到零．从图6、图7可以看出,7个系统的自适应参数以及控制器能够随着机动参数的变化而变化并且逐渐稳定．因此,定理1和定理2通过数值仿真得到了验证．

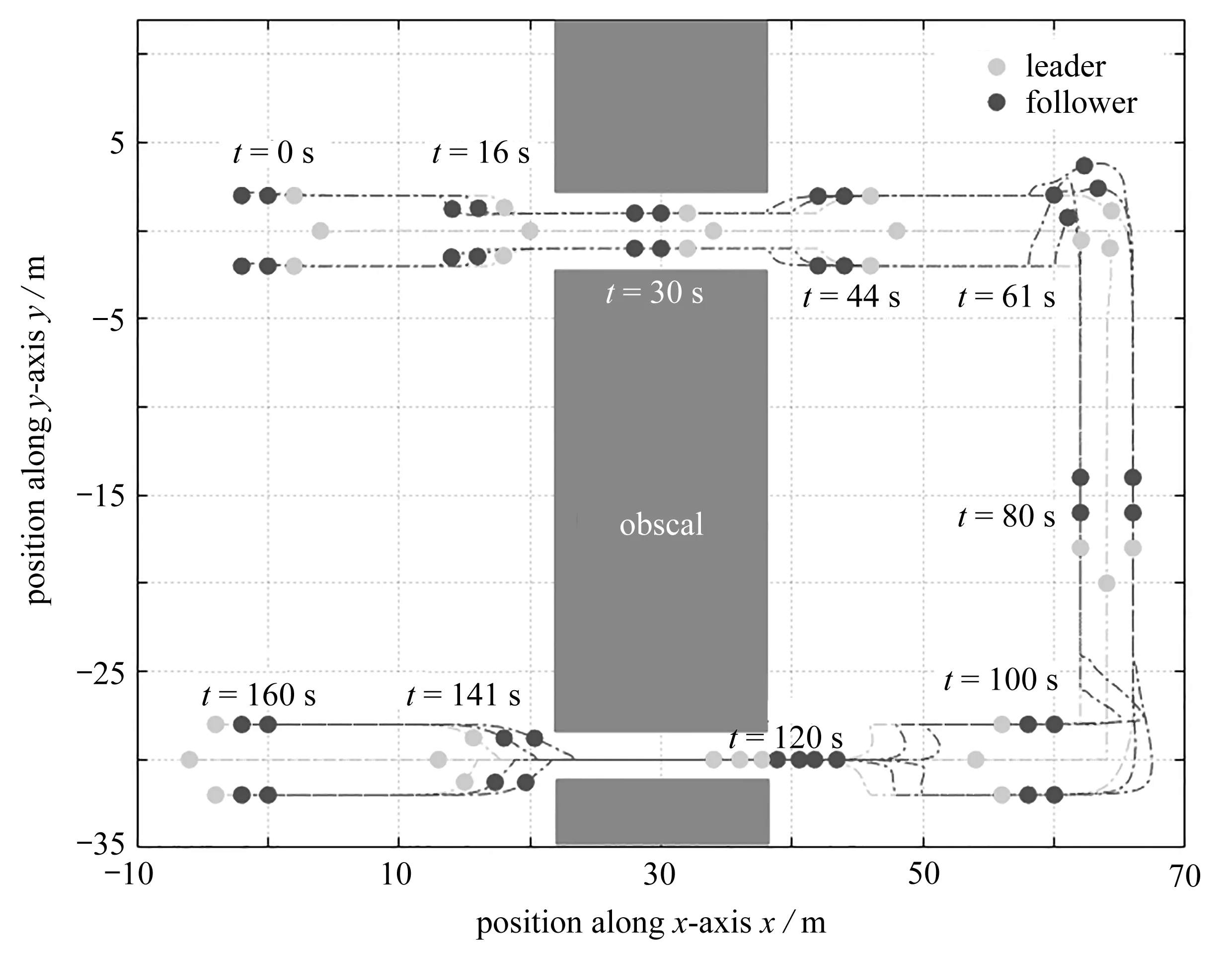
图3 不同时刻系统的运动状态Fig. 3 Motion states of the 7 agents at different moments

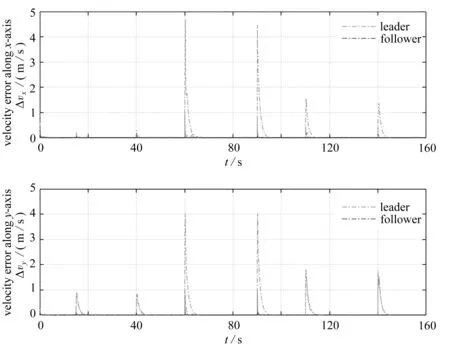
图5 系统的追踪速度误差Fig. 5 Tracking velocity errors of the system

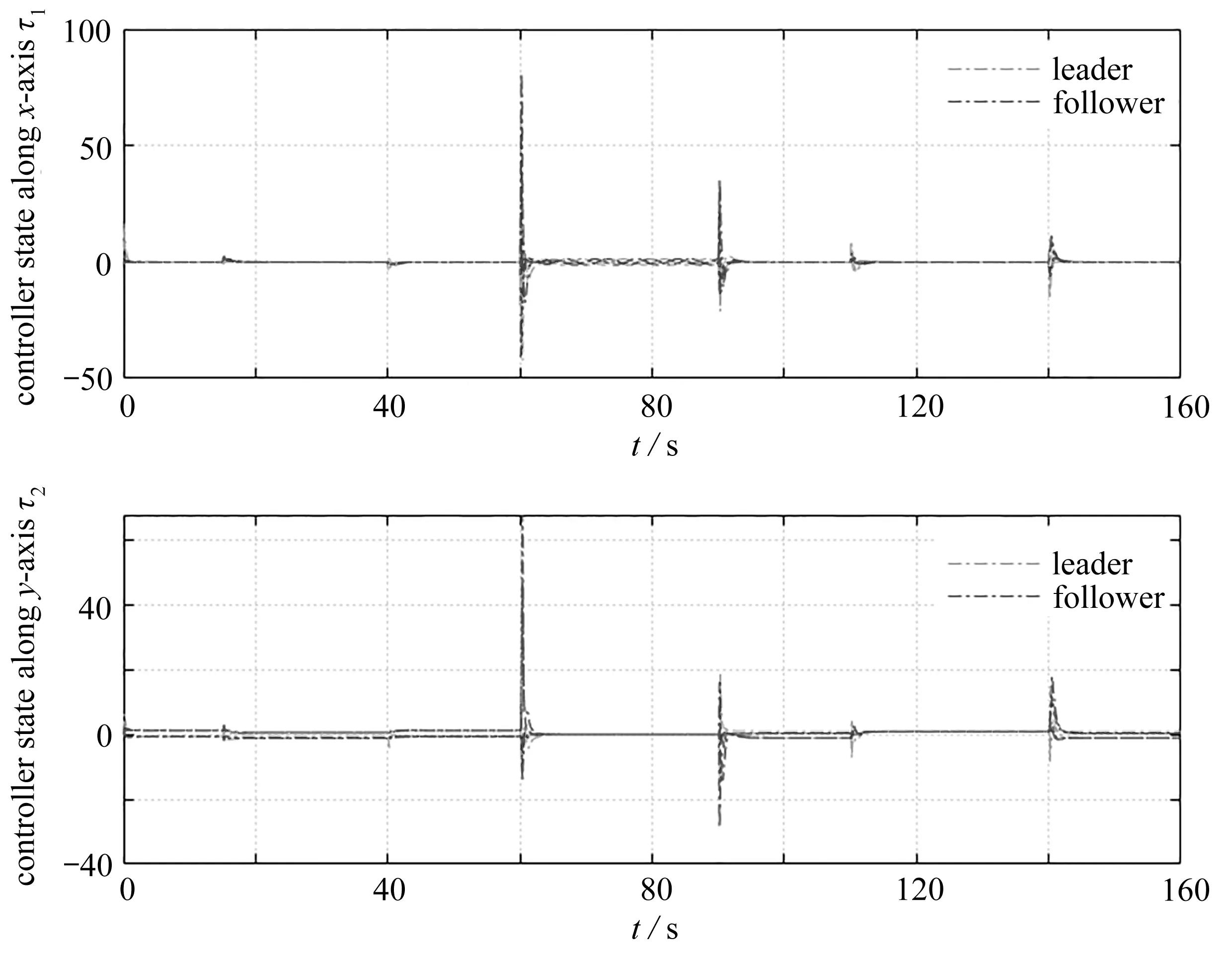
图6 不同时刻系统的控制器状态Fig. 6 Controller states of the 7 agents at different moments

图7 系统的自适应参数状态Fig. 7 Adaptive parameter states of the 7 agents at different moments

4 结 论

本文研究了在有向网络拓扑下, 具有领航者的不确定性网络化Euler-Lagrange系统的编队机动控制问题．基于经典的滑模控制理论与代数图矩阵理论构造了不确定性网络化Euler-Lagrange系统的编队机动控制策略．该算法中跟随者不需要知道机动参数,且编队的标称队形可以是一般或者凸标称结构,也可以是非一般和非凸标称结构．最后通过数值仿真,验证了所提算法的可行性．

致谢本文作者衷心感谢太原理工大学2022年校专项/青年基金(2022QN100)对本文的资助．