一类随机微分方程的随机源反演方法和性质
陈 琛, 冯晓莉, 陈汉章
(西安电子科技大学 数学与统计学院, 西安 710126)
0 引 言
众所周知,反问题的应用非常广泛,相应的研究成果也越来越多[1-5].然而,绝大多数反问题都是不适定的,尤其是稳定性往往不成立,这也是研究反问题的困难和意义所在.不仅如此,实际应用中会有很多随机因素的影响,比如测量数据带有噪声,数学模型的建立含有模型误差等.这些因素对于不适定反问题的研究不容小觑,否则求得的数值结果会出现灾难性的问题.一种自然而又巧妙的处理方法是将这些因素视为随机的,相应的问题就看作随机问题.此外,随机技术的引入可以很好地耦合不同度量尺度之间的干扰[6-9].综上可知,关于随机反问题的研究既非常重要又很有实际意义.
本文关心的是如下一类随机微分方程:
(1)
其中a(x),h(t)已知,且a(x)≢0,h(t)≥h0>0,D=(0,1),BH(t)为概率空间(Ω,F,{Ft}t≥0,)上的分式Brown运动,H∈(0,1)为Hurst参数,为彩噪声.为了简便,后文将u(x,t,ω)简记为u(x,t).本文主要探讨:
(P1) 正问题 已知φ(x),ψ(x),求温和解u(x,t);
(P2) 反问题 给定T时刻的样本数据u(x,T,ω), 反演问题(1)中随机源项的部分统计量φ(x)和ψ2(x).
对于正问题(P1),由于随机源项F(x,t)的低正则性[10],该方程不是几乎处处存在的,所以方程的适定性与经典意义下截然不同,相应的解在什么样的空间存在是值得研究的.而关于反问题(P2),F(x,t)为随机场,如何由u(x,t,ω)的统计量来反演F(x,t)的统计量φ(x)与ψ2(x)是很困难且有意义的,而其不适定性又将使得该反问题的求解难上加难.
由于以上的众多原由,近年来反随机源问题倍受学者们的重视[11-12],关于分式Brown运动驱动下的随机微分方程的反源问题,例如,随机的时空分数阶方程[13],随机波动方程[14],一个随机的时间分数阶扩散方程[15],一维随机对流扩散方程[16]等已有一些研究结果.这些工作均先是利用Laplace 变换或Fourier变换或广义Fourier 级数展开得到相应的温和解,然后再进一步讨论.本文所要讨论的问题(1),是一种更为广泛的随机问题,比如随机热方程:
(2)
其中L为一致椭圆算子.借助于广义Fourier级数展开,问题(2)可转化为
(3)

1 理 论 基 础
定义1[15,17]设0 则称BH(t)为分式Brown运动,其中H是Hurst参数,E[·]表示期望.特别地,当H=1/2时,即为标准Brown运动B(t). 对于分式Brown运动BH(t),其中H∈(0,1),相应的随机积分有如下公式[15]: 2) 当H∈(0,1/2)时, (4) 其中 3) 当H=1/2时, (5) 4) 当H∈(1/2,1)时, (6) 其中αH=H(2H-1). 不难得到问题(1)的温和解如下. 定义2 一个随机过程u∈L2(D)称为问题(1)的温和解,如果 (7) 几乎处处成立. 下面进一步说明在一定条件下,温和解u(x,t)是适定的.为了推导的方便,先给出如下引理. 引理1[15]当H∈(0,1/2)时,对∀t>τ有 由式(7)知, 2I1(t)+2I2(t). (8) 由h(t)≥h0>0及积分中值定理可知,存在某个ξ∈(0,t),有 其中 若令M(x)max{1,e-a(x)T},则 关于I2(t),有 情形1 当H∈(0,1/2)时,由式(4)可知 J1(t)+J2(t)+J3(t), (9) 这里“ab”表示a≤Cb,其中C为某个正常数.显然有 (10) (11) 由引理1可知 J2(t)τ1-2H(t4H-2+τ4H-2)dτ·M2(x)t2HM2(x). 关于J3(t),由于 1) 当|a(x)|≤1时, |e-a(x)(t-u)-e-a(x)(t-τ)|≤|a(x)|M(x)|u-τ|≤M(x)|u-τ|; 2) 当|a(x)|>1时, 根据∂KH(u,τ)/∂u的表达式,易得 (12) 将式(10)—(12)代入式(9),可得 此时有 情形2 当H=1/2时,由式(5)可知 所以 情形3 当H∈(1/2,1)时,由式(6)可知 (13) 因此 综上可知如下定理成立. 定理1 如果函数f(x),g(x)∈L2(D),则有估计式 注1 由定理1可知:1) 若a(x)有界,则‖M‖L∞(D)也有界;2) 若a(x)≥0,则‖M‖L∞(D)亦有界;3) 若a(x)→-∞,则‖M‖L∞(D)无界.因此第1)、2)两种情况下问题(1)的解是稳定的,但第3)种情况下问题(1)的解不稳定. 本节我们考虑通过u(x,T,ω)的统计量来反演问题(1)随机源项中的统计量φ(x)和ψ2(x).若h(t)≡1时,φ(x)和ψ2(x)就是随机源项的期望和方差.由式(7)可知 (14) (15) 其中var(·)表示方差. 进一步可得 (16) 下面分析由式(14)和(15)来反演φ(x)与ψ2(x)的唯一性与稳定性如何. 由h(τ)≥h0>0易知,对于固定的x,总有 情形1 当H∈(0,1/2)时, 对于固定的x,当a(x)≥0时,e-a(x)(T-s)关于s是递增的,所以 e-a(x)(T-u)-e-a(x)(T-τ)≥0. 又由KH(u,τ)的表达式可知KH(T,τ)与∂KH(u,τ)/∂u均大于0且连续,所以一定存在一个c1(x)>0,有 当a(x)<0时,e-a(x)(T-s)关于s是递减的,所以(d/ds)e-a(x)(T-s)<0,此时 根据分部积分,可知 由e-a(x)(T-s)关于s是递减的,且KH(u,τ)>0,可知 (17) 情形2 当H=1/2时,由It等距公式(5)可知:当a(x)≥0时,有 当a(x)<0时,有 (18) 情形3 当H∈(1/2,1)时,有 当a(x)≥0时,有 注意到式(13),有 当a(x)≤0,类似地有 (19) 综上分析可知,如下定理成立. 定理2 若φ(x),ψ(x)∈L2(D)且‖ψ‖L2(D)≠0,h(x)≥h0>0,h(x)∈L∞(0,T),则源项中φ(x)与ψ2(x)能由u(x,T,ω)的期望和方差唯一确定. 反源问题在医学、地质勘探等方面都有非常广泛的应用,然而反源问题往往是不稳定的.本小节将分析反演φ(x)与ψ2(x)时的稳定性.先分析a(x)>0时的稳定性. 一方面,我们有 情形1 若a(x)>1/T2,由式(9)可知 对于H∈(0,1/2),借助于不等式 (20) 有 根据式(20)易得 并且 因此 此外, J21(T)+J22(T)+J23(T). 根据引理1,有 利用证明引理1相同的方法,我们得到 同样地,利用引理1,有 所以,对于J2(T),我们有 此外, 因此 对于H=1/2,利用It等距公式(5)并注意到a(x)>1/T2可得 对于H∈(1/2,1),利用式(6)并注意到估计式(20),将其化为4个部分,每个部分分别借用估计式(20)进行计算,所以有 其中 由于对称性 因此 对于H=1/2,利用It等距公式(5)易得 对于H∈(1/2,1),利用公式(6)并进行简单的计算可得 综合本小节的推导以及3.1小节中的式(17)—(19),我们得到以下定理. 定理3 对于任意的a(x),有估计式 对于a(x)≥1/T2,有 对于a(x)<0或0 注2 由定理3可知,当a(x)<0或0 本文讨论了一类随机微分方程的反源问题,根据方程的温和解,讨论了正问题的适定性.利用温和解的统计性质,根据T时刻的数据反演方程的源项,证明了源项反演的唯一性,并分析了关于源项φ(x)和ψ2(x)反演的稳定性情况.后面我们将进一步考虑相应的数值结果.2 正 问 题
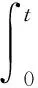

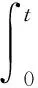
3 反 问 题
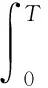
3.1 唯一性
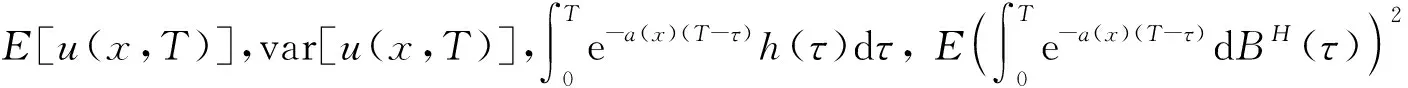
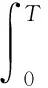
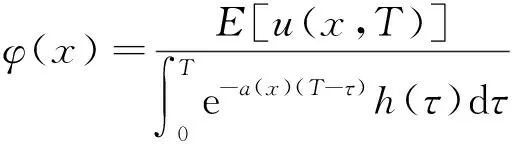

3.2 稳定性分析

4 结 论

