立方准晶压电材料的半空间问题

李光芳, 刘昉昉, 于 静, 李联和

(1. 内蒙古农业大学 理学院, 呼和浩特 010018;2. 内蒙古自治区应用数学中心, 呼和浩特 010022;3. 内蒙古师范大学 数学科学学院, 呼和浩特 010022)

0 引 言

1984年,以色列科学家Shechtman采用急速冷凝法研究Al-Mn合金时发现了准晶材料[1],其具有准周期的长程平移对称性和取向对称性．由于准晶材料特殊的物理性能,使其具有广泛的应用前景．Ding等[2]建立了准晶线弹性理论．范天佑[3]通过引入复变量或广义复变量,研究了若干准晶断裂力学问题．郭俊宏等[4]构造保角映射,解决了一维六方准晶材料中含双裂纹的椭圆孔口反平面剪切问题．Li等[5]研究了十八次对称准晶体的弹性问题．肖万伸等[6]研究了一维六方准晶复合材料夹杂界面层中螺型位错与夹杂以及无限大基体的干涉效应．Wang等[7]研究了均匀十次准晶材料裂纹尖端附近的弹性场．Zhang等[8]研究了二维六方准晶材料半空间上的摩擦接触问题和半平面黏着接触问题．

压电效应是准晶材料重要的物理性质之一,在其应用中可能会遇到复杂的机电负载,因此研究准晶压电材料对外部施加载荷的响应非常重要．文献[9-10]发展了准晶压电材料的线弹性理论．Zhang等[11]获得了一维正交压电准晶材料平面弹性问题的一般解．Li等[12]采用算子理论方法获得了一维六方压电准晶的三维弹性问题的一般解．Fan等[13]发展了含复杂缺陷一维六方压电准晶的间断有限元方法．白巧梅等[14]利用复变函数方法得到了一维六方准晶压电材料裂纹尖端的应力分布和场强度因子的解析表达式．Li等[15]研究了考虑热效应的一维六方压电准晶中的三维裂纹问题．刘兴伟等[16]利用复变函数方法研究了一维六方压电准晶中正n边形孔边裂纹的反平面问题．Cheng等[17]利用Trefftz方法研究了一维六方压电准晶反平面断裂问题．目前,关于三维准晶弹性问题的研究较少,然而实际应用中三维准晶材料的占比非常高．周旺民等[18]考虑了立方准晶中的位错诱导弹性场．Gao等[19]采用复变函数方法研究了含椭圆孔立方准晶断裂力学问题．Li等[20]研究了三维二十面体准晶的Stroh形式,并将其应用于位错问题的研究．Long等[21]研究了立方准晶圆盘的热弹性问题．三维准晶半空间问题的Green函数解是研究层合材料、界面问题等实际问题的理论基础,尚未看到有关研究．

本文研究了在反平面机械载荷和面内电载荷作用下立方准晶压电材料的半空间问题．首先给出了控制方程,然后采用复变函数方法,对半无限域区域表面边界条件进行积分,获得了立方准晶压电材料半空间问题的基本解．在此基础上,给出了集中线力作用下立方准晶压电材料半空间问题应力、位移的解析表达式．

1 立方准晶压电材料的基本方程

在空间直角坐标系下,立方准晶压电材料反平面问题的本构方程为[22]

(1)

其中σij,εij分别表示声子场的应力、应变;Hij,ωij分别表示相位子场的应力、应变;Di表示电位移;Ei表示电场强度;C44为声子场弹性常数;K44为相位子场弹性常数;R3为声子场与相位子场耦合常数;e14和d123分别为声子场和相位子场压电常数;λ11为介电常数．

平衡方程为(不考虑体力的情况)

σiz,i=0,Hiz,i=0,Di,i=0,i=x,y;

(2)

几何方程为

(3)

其中uz表示声子场位移,wz表示相位子场位移,Φ表示电势．

由方程(1)—(3)可以获得由位移和电势表示的控制方程：

(4)

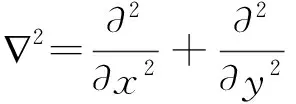
方程(4)可以改写为[13]

AU=0,

(5)

其中U=(uz,wz,Φ)T,A是微分算子矩阵,

(6)

由方程(6)可知A的行列式为

(7)

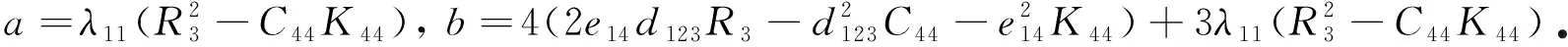
下面我们引入位移函数F,其满足方程

(8)

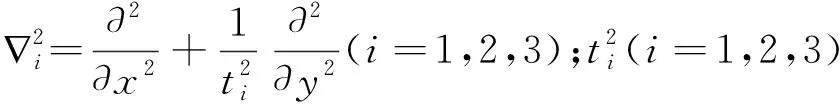
根据算子理论,方程(5)的一般解可表示为

uz=Ai1F,wz=Ai2F,Φ=Ai3F,i=1,2,3．

(9)

取i=2,由方程(6)可知|A|的代数余子式为

(10)

把方程(10)代入方程(9)得

(11)

(12)

(13)

假设复函数F(x,y)的形式为F(x,μy),则μ须满足如下特征方程[23]：

aμ6+bμ4+bμ2+a=0．

(14)

方程(14)有6个纯虚数根：

μ4=-μ1,μ5=-μ2,μ6=-μ3,

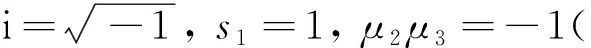
根据解析函数的性质和方程(8),位移函数F可以表示为

(15)

其中Re(·)表示实部,Fk(zk)为关于zk=x+μky(k=1,2,3)的任意解析函数．结合方程(1)、(3)、(11)、(12)、(13)可知,应力和电位移的复表示为

(16)

(17)

(18)

(19)

(20)

(21)

其中

2 立方压电准晶材料半空间问题基本解

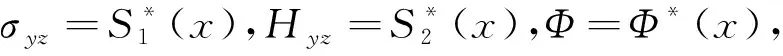
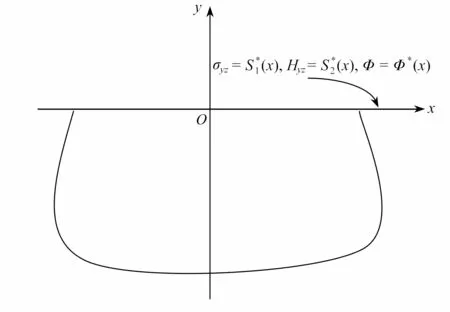
图1 力电载荷作用下的半无限区域Fig. 1 The semi-infinite region under electromechanical load

由于当y=0时,z1=z2=z3=ξ,ξ为实数,则方程(13)、(16)、(18)可以改写为

(22)

其中

对方程(22)积分可得

(23)

其中ai(i=1,2,3)为常数(见附录)．方程(23)为立方压电准晶材料半空间问题基本解,结合边界条件,可以得到弹性场分析．作为具体应用,下面讨论集中线力作用下立方压电准晶材料半空间问题．

3 集中线力作用在半空间表面

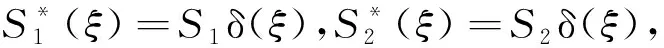
(24)

(25)

(26)

由方程(24)—(26)可得声子场和相位子场的位移、电势表达式为

(27)

(28)

(29)

其中ai(i=4,5,…,8)为常数(见附录)．当不考虑相位子场时,声子场位移表达式可以退化为

(30)

且电势处处为零,与文献[24]结果一致．由方程(24)—(26)也可得到声子场和相位子场应力及电位移表达式(见附录)．

下面讨论声子场位移、相位子场位移和电势分布情况,材料常数为[12]

C44=5.0×1010N·m-2,K44=3×108N·m-2,R3=1.2×109N·m-2,

e14=-0.138 C·m-2,d123=-0.16 C·m-2,λ11=8.26×10-11C2·N-1·m-2,

S1=2 000 N·m-1,S2=2 500 N·m-1．

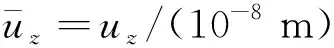
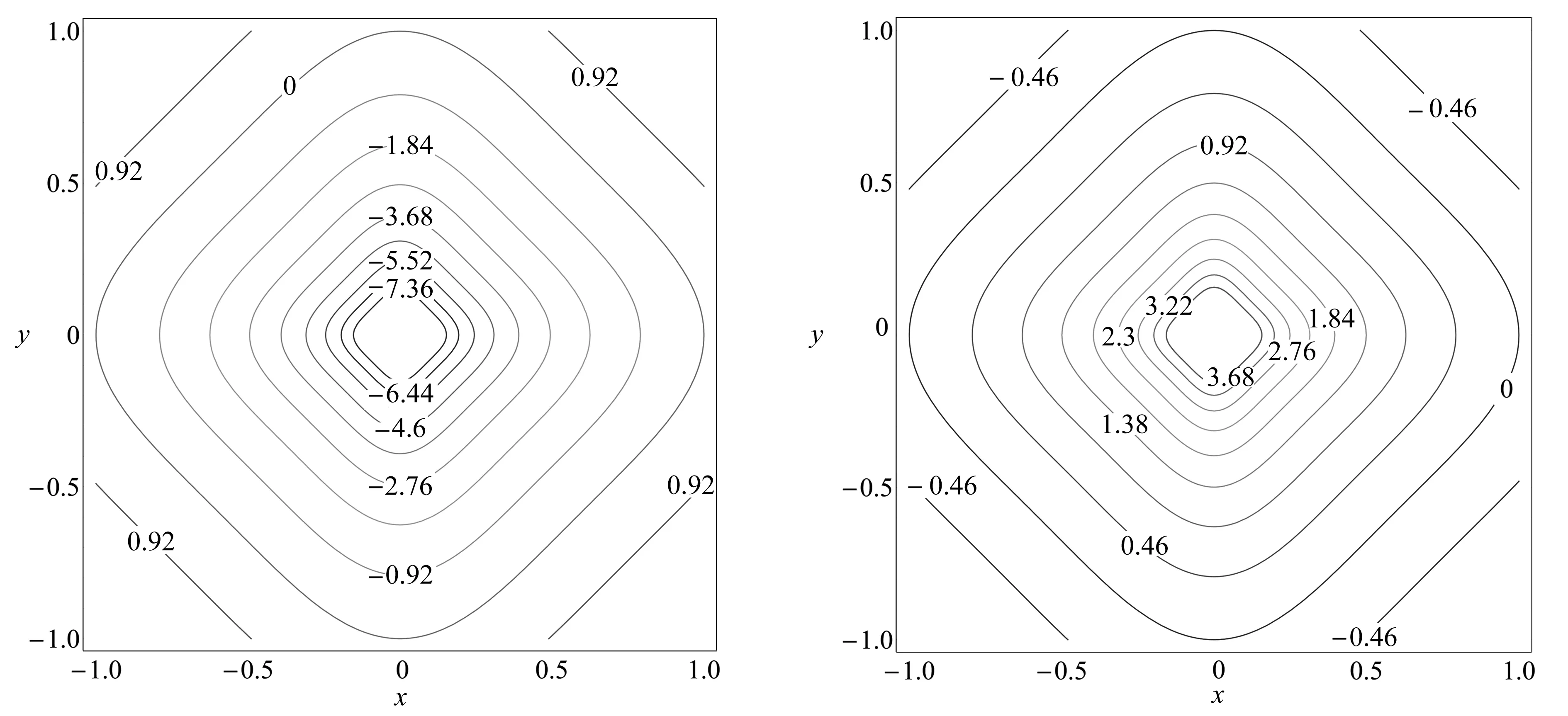
图2 无量纲声子场位移等势图 图3 无量纲相位子场位移等势图Fig. 2 The contour of dimensionless phonon field displacement

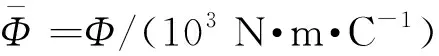
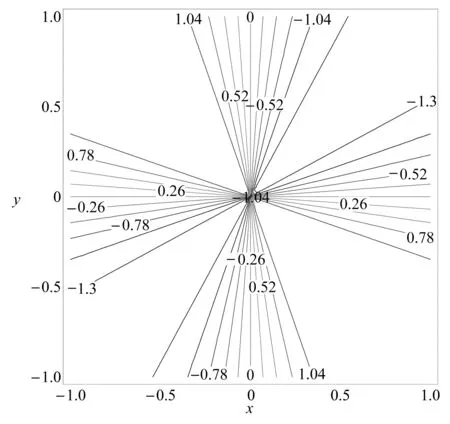
图4 无量纲电势等势图Fig. 4 The contour of dimensionless potential

4 结 论

本文采用复变函数方法获得了反平面机械载荷和面内电载荷作用下,立方准晶压电材料半空间问题的基本解．在此基础上,给出了集中线力作用下,立方准晶压电材料半空间问题的位移、应力和电场的解析表达式,并用数值结果说明了声子场、相位子场位移和电势的分布情况．本文获得的立方准晶压电材料半空间问题的基本解可应用于其他半空间边值问题的研究中．

致谢本文作者衷心感谢内蒙古师范大学基本科研业务费(2022JBZD010; 2022JBXC013)、内蒙古农业大学基础学科科研启动基金项目(JC2020002)和内蒙古师范大学研究生科研创新基金(CXJJB22011)对本文的资助．

附 录

a4=4a1(d123S1-e14S2),

a5=a1(a2S1+S2),

其中

b1=2(C44d123-e14R3),

b2=2(e14K44-d123R3),